智慧優化演演算法:麻雀搜尋演演算法-附程式碼
2020智慧優化演演算法:麻雀搜尋演演算法
摘要:麻雀搜尋演演算法(Sparrow Search Algorithm, SSA)是於2020年提出的。SSA 主要是受麻雀的覓食行為和反捕食行為的啟發而提出的。該演演算法比較新穎,具有尋優能力強,收斂速度快的優點
1.演演算法原理
建立麻雀搜尋演演算法的數學模型,主要規則如下所述:
- 發現者通常擁有較高的能源儲備並且在整個種群中負責搜尋到具有豐富食物的區域,為所有的加入者提供覓食的區域和方向。在模型建立中能量儲備的高低取決於麻雀個體所對應的適應度值(Fitness Value)的好壞。
- 一旦麻雀發現了捕食者,個體開始發出鳴叫作為報警訊號。當報警值大於安全值時,發現者會將加入者帶到其它安全區域進行覓食。
- 發現者和加入者的身份是動態變化的。只要能夠尋找到更好的食物來源,每隻麻雀都可以成為發現者,但是發現者和加入者所佔整個種群數量的比重是不變的。也就是說,有一隻麻雀變成發現者必然有另一隻麻雀變成加入者。
- 加入者的能量越低,它們在整個種群中所處的覓食位置就越差。一些飢腸轆轆的加入者更有可能飛往其它地方覓食,以獲得更多的能量。
- 在覓食過程中,加入者總是能夠搜尋到提供最好食物的發現者,然後從最好的食物中獲取食物或者在該發現者周圍覓食。與此同時,一些加入者為了增加自己的捕食率可能會不斷地監控發現者進而去爭奪食物資源。
- 當意識到危險時,群體邊緣的麻雀會迅速向安全區域移動,以獲得更好的位置,位於種群中間的麻雀則會隨機走動,以靠近其它麻雀。
在模擬實驗中,我們需要使用虛擬麻雀進行食物的尋找,由n只麻雀組成的種群可表示為如下形式:
X
=
[
x
1
1
x
1
2
.
.
.
x
1
d
x
2
1
x
2
2
.
.
.
x
2
d
.
.
.
.
.
.
.
.
.
.
.
.
x
n
1
x
n
2
.
.
.
x
n
d
]
(1)
X=\left[\begin{matrix} x_1^1&x_1^2&...&x_1^d\\ x_2^1&x_2^2&...&x_2^d\\ ...&...&...&... \\ x_n^1&x_n^2&...&x_n^d\\ \end{matrix}\right]\tag{1}
X=⎣⎢⎢⎡x11x21...xn1x12x22...xn2............x1dx2d...xnd⎦⎥⎥⎤(1)
其中,
d
d
d 表示待優化問題變數的維數,
n
n
n 則是麻雀的數量。那麼,所有麻雀的適應度值可以表示為如下形式:
F
x
=
[
f
(
[
x
1
1
x
1
2
.
.
.
x
1
d
]
)
f
(
[
x
2
1
x
2
2
.
.
.
x
2
d
]
)
.
.
.
f
(
[
x
n
1
x
n
2
.
.
.
x
n
d
]
)
]
(2)
F_x =\left[\begin{matrix} f([x_1^1&x_1^2&...&x_1^d])\\ f([x_2^1&x_2^2&...&x_2^d])\\ ... f([x_n^1&x_n^2&...&x_n^d]) \end{matrix}\right]\tag{2}
Fx=⎣⎡f([x11f([x21...f([xn1x12x22xn2.........x1d])x2d])xnd])⎦⎤(2)
其中,f 表示適應度值。
在 SSA 中,具有較好適應度值的發現者在搜尋過程中會優先獲取食物。此外,因為發現者負責為整個麻雀種群尋找食物併為所有加入者提供覓食的方向。因此,發現者可以獲得比加入者更大的覓食搜尋範圍。根據規則(1)和規則(2),在每次迭代的過程中,發現者的位置更新描述如下:
X
i
,
j
t
+
1
=
{
X
i
,
j
.
e
x
p
(
−
i
α
.
i
t
e
r
m
a
x
)
,
i
f
R
2
<
S
T
X
i
,
j
+
Q
.
L
,
i
f
R
2
≥
S
T
(3)
X_{i,j}^{t+1}=\begin{cases} X_{i,j}.exp(-\frac{i}{\alpha.iter_{max}}),if\, R_2<ST\\ X_{i,j} + Q.L,if\, R_2\geq ST \end{cases}\tag{3}
Xi,jt+1={Xi,j.exp(−α.itermaxi),ifR2<STXi,j+Q.L,ifR2≥ST(3)
其中,
t
t
t 代表當前迭代數,
j
=
1
,
2
,
3
,
.
.
.
,
d
j =1, 2, 3, . . . , d
j=1,2,3,...,d。
i
t
e
m
m
a
x
item_{max}
itemmax
是一個常數,表示最大的迭代次數。
X
i
j
X_{ij}
Xij表示第
i
i
i 個麻雀在第
j
j
j 維中的位置資訊。
α
∈
(
0
,
1
]
α∈(0, 1]
α∈(0,1]是一個亂數。
R
2
(
R
2
∈
[
0
,
1
]
)
R_2(R_2∈[0,1])
R2(R2∈[0,1])和
S
T
(
S
T
∈
[
0.5
,
1
]
)
ST(ST∈[0.5,1])
ST(ST∈[0.5,1])分別表示預警值和安全值。
Q
Q
Q 是服從正態分佈的亂數。
L
L
L 表示一個
1
×
d
1×d
1×d 的矩陣,其中該矩陣內每個元素全部為 1。
當 R 2 < S T R2< ST R2<ST 時,這意味著此時的覓食環境周圍沒有捕食者,發現者可以執行廣泛的搜尋操作。如果 R 2 ≥ S T R2≥ ST R2≥ST,這表示種群中的一些麻雀已經發現了捕食者,並向種群中其它麻雀發出了警報,此時所有麻雀都需要迅速飛到其它安全的地方進行覓食。
對於加入者,它們需要執行規則(3)和規則(4)。如前面所描述,在覓食過程中,一些加入者會時刻監視著發現者。一旦它們察覺到發現者已經找到了更好的食物,它們會立即離開現在的位置去爭奪食物。如果它們贏了,它們可以立即獲得該發現者的食物,否則需要繼續執行規則(4)。加入者的位置更新描述如下:
X
i
,
j
t
+
1
=
{
Q
.
e
x
p
(
X
w
o
r
s
t
−
X
i
,
j
t
i
2
)
,
i
f
i
>
n
/
2
X
P
t
+
1
+
∣
X
i
,
j
−
X
P
t
+
1
∣
.
A
+
.
L
,
o
t
h
e
r
w
i
s
e
(4)
X_{i,j}^{t+1}=\begin{cases} Q.exp(\frac{X_{worst}-X_{i,j}^t}{i^2}),if\, i>n/2\\ X_P^{t+1}+ |X_{i,j} - X_P^{t+1}|.A^{+}.L,otherwise \end{cases}\tag{4}
Xi,jt+1={Q.exp(i2Xworst−Xi,jt),ifi>n/2XPt+1+∣Xi,j−XPt+1∣.A+.L,otherwise(4)
其中,
X
p
X_p
Xp是目前發現者所佔據的最優位置,
X
w
o
r
s
t
X_{worst}
Xworst則表示當前全域性最差的位置。
A
A
A表示一個
1
×
d
1×d
1×d 的矩陣,其中每個元素隨機賦值為 1 或-1,並且
A
+
=
A
T
(
A
A
T
)
−
1
A^+=A^T(AA^T)^{-1}
A+=AT(AAT)−1。當i >n/2 時,這表明,適應度值較低的第 i 個加入者沒有獲得食物,處於十分飢餓的狀態,此時需要飛往其它地方覓食,以獲得更多的能量。
在模擬實驗中,我們假設這些意識到危險的麻雀佔總數量的 10% 到 20%。這些麻雀的初始位置是在種群中隨機產生的。根據規則(5),其數學表示式可以表示為如下形式:
X
i
,
j
t
+
1
=
{
X
b
e
s
t
t
+
β
.
∣
X
i
,
j
t
−
X
b
e
s
t
t
∣
,
i
f
f
i
>
f
g
X
i
,
j
t
+
K
.
(
∣
X
i
,
j
t
−
X
w
o
r
s
t
t
∣
(
f
i
−
f
w
)
+
ε
)
,
i
f
f
i
=
f
g
(5)
X_{i,j}^{t+1}=\begin{cases} X_{best}^t + \beta.|X_{i,j}^t - X_{best}^t|,if\, f_i>f_g\\ X_{i,j}^t + K.(\frac{|X_{i,j}^t - X_{worst}^t|}{(f_i -f_w)+\varepsilon}), if\, f_i =f_g \end{cases}\tag{5}
Xi,jt+1={Xbestt+β.∣Xi,jt−Xbestt∣,iffi>fgXi,jt+K.((fi−fw)+ε∣Xi,jt−Xworstt∣),iffi=fg(5)
其中,其中
X
b
e
s
t
X_{best}
Xbest是當前的全域性最優位置。
β
β
β 作為步長控制引數,是服從均值為 0,方差為 1 的正態分佈的亂數。
K
∈
[
−
1
,
1
]
K∈[-1,1]
K∈[−1,1]是一個亂數,fi則是當前麻雀個體的適應度值。
f
g
f_g
fg和
f
w
f_w
fw分別是當前全域性最佳和最差的適應度值。
ε
\varepsilon
ε 的常數,以避免分母出現零。
為簡單起見,當 f i > f g f_i >f_g fi>fg表示此時的麻雀正處於種群的邊緣,極其容易受到捕食者的攻擊。 X b e s t X_{best} Xbest表示這個位置的麻雀是種群中最好的位置也是十分安全的。 f i = f g f_i = f_g fi=fg時,這表明處於種群中間的麻雀意識到了危險,需要靠近其它的麻雀以此儘量減少它們被捕食的風險。 K K K 表示麻雀移動的方向同時也是步長控制引數。
演演算法流程
Step1: 初始化種群,迭代次數,初始化捕食者和加入者比列。
Step2:計算適應度值,並排序。
Step3:利用式(3)更新捕食者位置。
Step4:利用式(4)更新加入者位置。
Step5:利用式(5)更新警戒者位置。
Step6:計算適應度值並更新麻雀位置。
Step7:是否滿足停止條件,滿足則退出,輸出結果,否則,重複執行Step2-6;
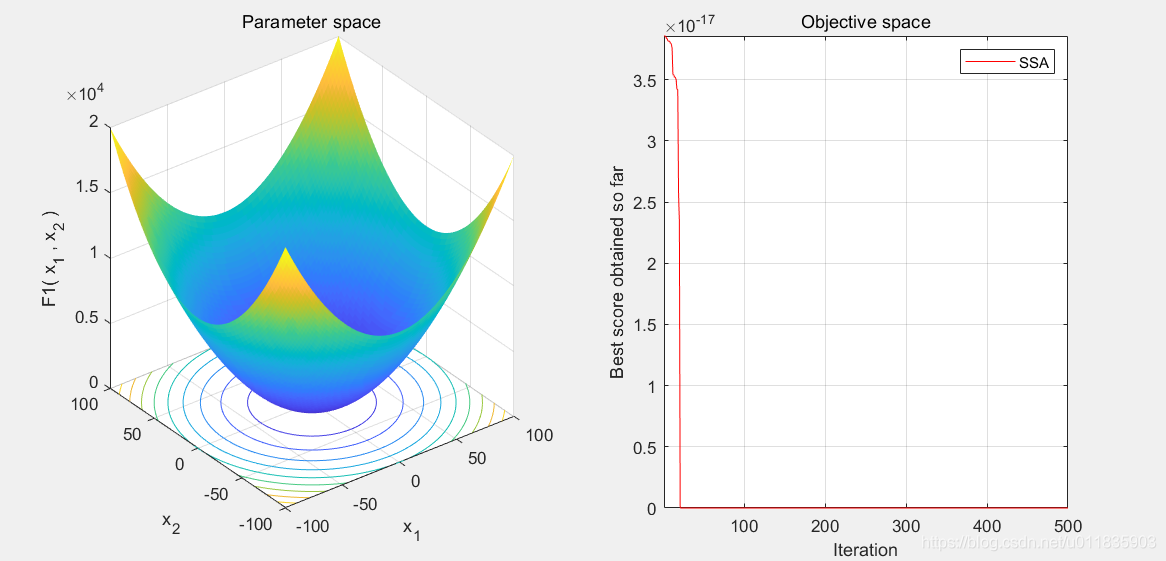
2.演演算法結果
3.參考文獻
[1] Xue J , Shen B . A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems ence & Control Engineering An Open Access Journal, 2020, 8(1):22-34.