技術文章 » buuoj-crypto 1

buuoj-crypto 1

2020-09-28 13:00:25

1.RSA

在一次RSA金鑰對生成中，假設p=473398607161，q=4511491，e=17，求d.
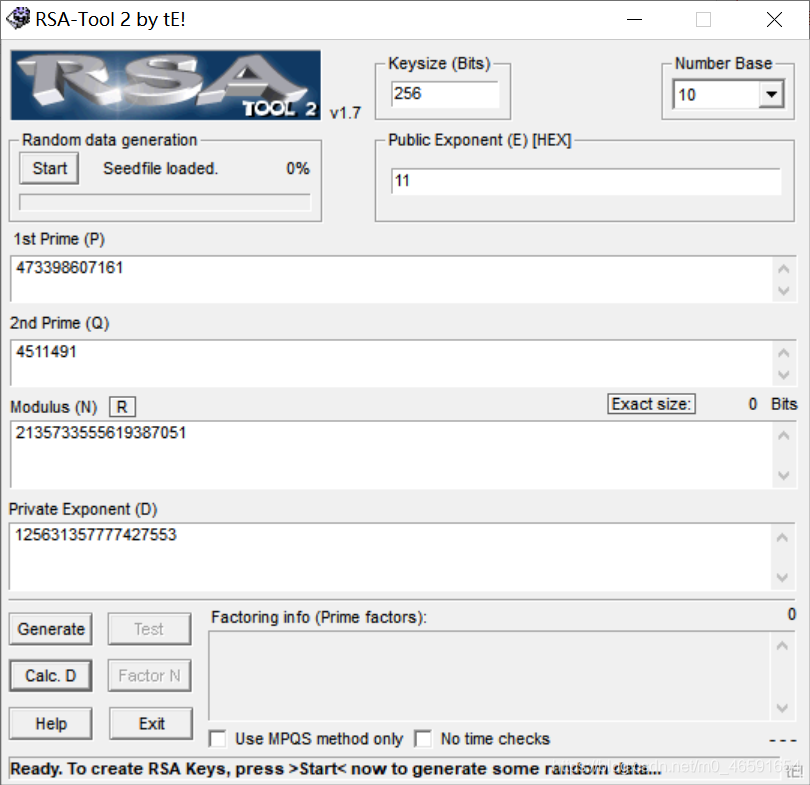
在這裡插入圖片描述

import gmpy2
p=473398607161
q=4511491
e=17
d = gmpy2.invert(e,(q-1)*(p-1))
print(d)

2.Alice與Bob

在這裡插入圖片描述
用分解大整數工具將98554799767分解為101999 · 966233，對新合成的數位101999966233進行md5的32位元小寫雜湊。
雜湊計算工具

3.rsarsa

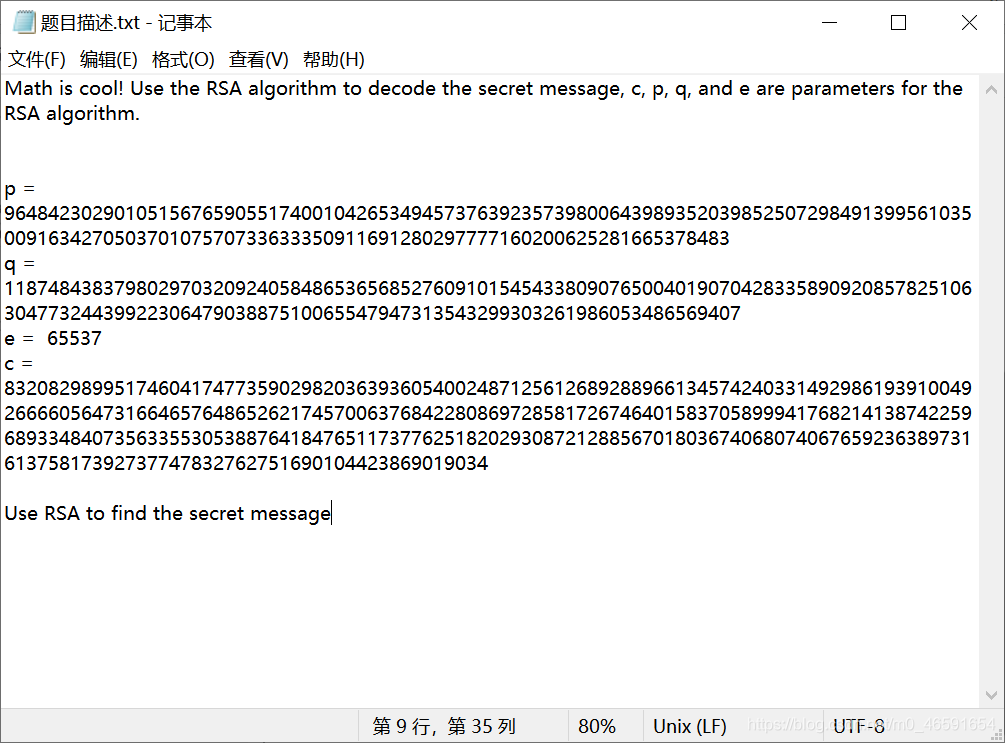
在這裡插入圖片描述
可用工具求出私鑰d=56632047571190660567520341028861194862411428416862507034762587229995138605649836960220619903456392752115943299335385163216233744624623848874235303309636393446736347238627793022725260986466957974753004129210680401432377444984195145009801967391196615524488853620232925992387563270746297909112117451398527453977
再用python函數pow()即可求出flag

e = 65537
p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
n = p*q

C = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

d = 56632047571190660567520341028861194862411428416862507034762587229995138605649836960220619903456392752115943299335385163216233744624623848874235303309636393446736347238627793022725260986466957974753004129210680401432377444984195145009801967391196615524488853620232925992387563270746297909112117451398527453977

M = pow(C,d,n)    #快速求冪取模運算
print(M)

4.大帝的密碼武器

題目：公元前一百年，在羅馬出生了一位對世界影響巨大的人物，他生前是羅馬三巨頭之一。他率先使用了一種簡單的加密函，因此這種加密方法以他的名字命名。
以下密文被解開後可以獲得一個有意義的單詞：FRPHEVGL
你可以用這個相同的加密向量加密附件中的密文，作為答案進行提交。
密文：ComeChina
用的是凱撒密碼，解密FRPHEVGL，當偏移量為13時，得到有意義的單詞security。
對ComeChina加密得到flag{PbzrPuvan}，要注意大小寫。

5.Windows系統密碼

在這裡插入圖片描述
MD5一個個解密，對ctf:1002:06af9108f2e1fecf144e2e8adef09efd:a7fcb22a88038f35a8f39d503e7f0062:::中的第二條32位元字元資料進行MD5解密，得到flag{good-luck}.

6.[BJDCTF 2nd]cat_flag

gif中兩種小貓分別對應二進位制數0和1，則下圖可用二進位制表示為
01000010010010100100010001111011010011010010000101100001001100000111111001111101
再將其轉換為字串得到BJD{M!a0~}.
在這裡插入圖片描述

7.[BJDCTF 2nd]燕言燕語-y1ng

題目：小燕子，穿花衣，年年春天來這裡，我問燕子你為啥來，燕子說:
79616E7A69205A4A517B78696C7A765F6971737375686F635F73757A6A677D2

考慮是個十六進位制序列，將其轉化為字串得yanzi ZJQ{xilzv_iqssuhoc_suzjg}.
猜測使用了維吉尼亞密碼，將yanzi作為金鑰進行解密得到BJD{yanzi_jiushige_shabi}

8.傳統知識+古典密碼

在這裡插入圖片描述
根據六十甲子相關數表得到各個年份對應的數位，根據提示，一甲子為60年，每個數位再加上60，得到八個數位88 90 83 68 77 70 76 90，猜測為ASCII碼，解碼得到XZSDMFLZ
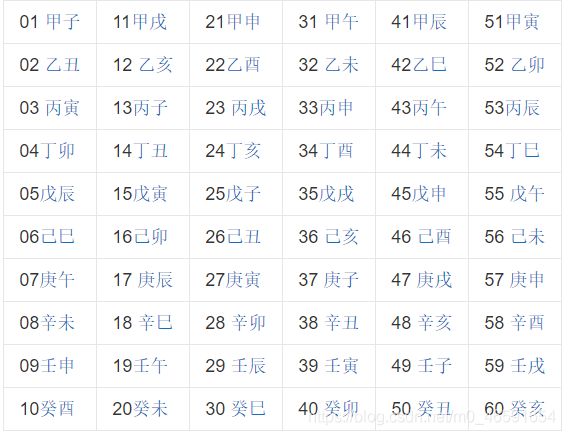
在這裡插入圖片描述
古典密碼就用柵欄和凱撒密碼一次嘗試，最後找到SHUANGYU

9.[GKCTF2020]小學生的密碼學

e(x)=11x+6(mod26)

密文：welcylk

（flag為base64形式）

觀察是仿射加密，解密得到sorcery
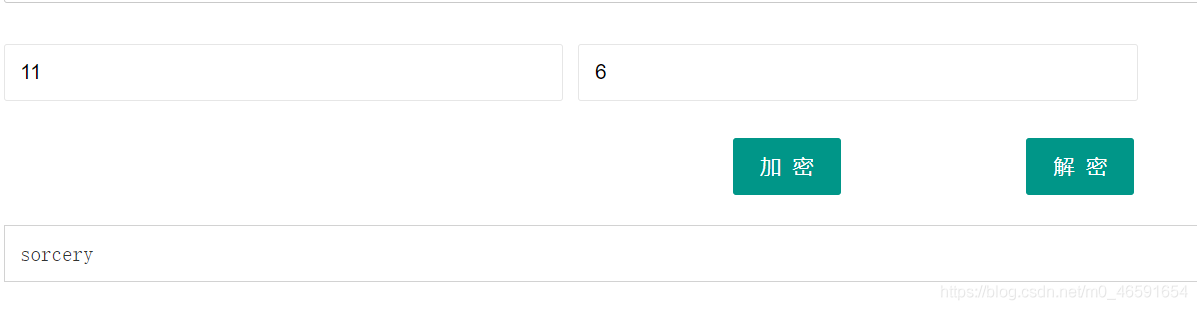
在這裡插入圖片描述

flag為base64形式，轉換一下得到flag{c29yY2VyeQ==}

10.資訊化時代的步伐

也許中國可以早早進入資訊化時代，但是被清政府拒絕了。附件中是數十年後一位偉人說的話的密文。請翻譯出明文(答案為一串中文！)
注意：得到的 flag 請包上 flag{} 提交
密文：606046152623600817831216121621196386

標準中文電碼：中國漢字多達6萬字，常用的漢字只有一萬個左右， 所以用10的4次方（10,000）來表示。中文電碼表採用了四位阿拉伯數位作代號，簡稱「四碼電報」，從0001到9999按四位數順序排列，用四位數位表示最多一萬個漢字、字母和符號。漢字先按部首，後按筆劃排列。字母和符號放到電碼表的最尾。

用中文電碼工具查詢對應中文得到：計算機要從娃娃抓起

11.[BJDCTF 2nd]靈能精通-y1ng

身經百戰的Y1ng已經達到崇高的武術境界，以自律克己來取代狂熱者的戰鬥狂怒與傳統的戰鬥形式。Y1ng所受的訓練也進一步將他們的靈能強化到足以瓦解周遭的物質世界。藉由集中這股力量，Y1ng能釋放靈能能量風暴來摧毀敵人的心智、肉體與器械。

給檔案新增字尾.jpg,得到圖片：

在這裡插入圖片描述
用到的是豬圈密碼的變形，聖堂武士密碼，解密得到flag{IMKNIGHTSTEMPLAR}。

豬圈密碼，一種以格子為基礎的簡單替代式密碼：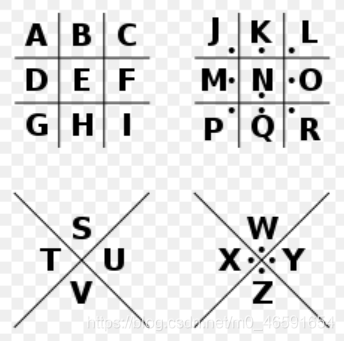
聖堂武士密碼(Templar Cipher)，共濟會的「豬圈密碼」的一個變種：
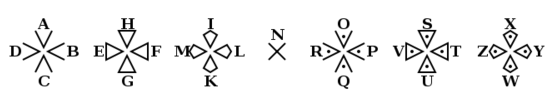
在這裡插入圖片描述

12.RSAROLL

題目給出了n,e,c，發現n比較小，可對n直接進行分解920139713 = 18443 · 49891，從而獲得該RSA的私鑰。

import gmpy2

n=920139713
e=19
c=[704796792,752211152,274704164,18414022,368270835,483295235,263072905,459788476,483295235,459788476,663551792,475206804,459788476,428313374,475206804,459788476,425392137,704796792,458265677,341524652,483295235,534149509,425392137,428313374,425392137,341524652,458265677,263072905,483295235,828509797,341524652,425392137,475206804,428313374,483295235,475206804,459788476,306220148]
p=18443
q=49891
phin=(p-1)*(q-1)
d=gmpy2.invert(e,phin)
flag=""
for i in c:
    flag=flag+chr(pow(i,d,n))
print(flag)
#flag{13212je2ue28fy71w8u87y31r78eu1e2}

13.壞蛋是雷賓

題目：老牌刺客之王混進了女王的住所。一天，女王得到了一個匿名舉報，說她的侍衛裡有一個刺客，叫做Rabin，而他的資訊就在一份檔案裡，檔案中有附帶一個Pk，是523798549，密文是162853095，校驗碼二進位制值是110001，根據說明是放在明文後一起加密的，明文與密文長度相同。加密演演算法和這位老牌刺客同名。快拯救女王，答案是求得的明文，進行32位元md5小寫雜湊字串，提交即可。 注意：得到的 flag 請包上 flag{} 提交。

觀察到n較小，可直接分解為：523798549 = 10663 · 49123

根據題意可知為Rabin演演算法。
Rabin是RSA衍生出來的一種演演算法。這種演演算法的特點在於e=2，加密方法是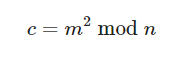在這裡插入圖片描述
而解密是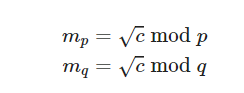在這裡插入圖片描述
然後用擴充套件歐幾里得計算出yq和yp，再用獲得的yq和yp解密四個密文
在這裡插入圖片描述
在這裡插入圖片描述

import gmpy2

n=523798549
p=10663
q=49123
c=162853095
inv_p = gmpy2.invert(p, q)
inv_q = gmpy2.invert(q, p)

mp = pow(c, 2666, p)
mq = pow(c, 12281, q)

a = (inv_p * p * mq + inv_q * q * mp) % n
b = n - int(a)
c = (inv_p * p * mq - inv_q * q * mp) % n
d = n - int(c)

for i in (a, b, c, d):
    print(bin(i)[2:])

得到了四個解，找到二進位制符合題目的解：10010011100100100101010110001，剔除校驗位110001。
轉十進位制再進行32位元md5小寫雜湊得到flag{ca5cec442b2734735406d78c88e90f35}