SBD演演算法詳解與相關python程式碼

本文為原創，轉載請註明出處，謝謝！

 

當涉及到延時情況，如kpi資料，在判斷兩兩特徵相關性的時候就不得不考慮SBD演演算法了。

通過SBD演演算法，我們可以在不清楚延遲的情況下找到兩組資料的相關性，以下來進行詳細講解。

 

SBD演演算法

       對於時間序列X(x1,x2,x3,…,xn)及時間序列Y(y1,y2,y3,…,yn)，兩序列間的存在時延為s的關係，計算兩條曲線相似度的SBD距離演演算法如下：

                  

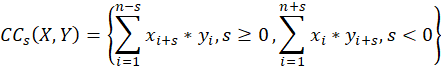
                  NCC(X,Y)=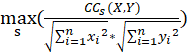

                  SBD(X,Y)=1-NCC(X,Y)

 

      其中，NCC為序列X,Y的標準化互相關係數，NCC的取值範圍在-1到1之間，與皮爾森相關係數類似。 所以最終計算的SBD演演算法結果在0到2之間，越靠近0時，兩組資料相關性越強。當SBD為0時，說明序列X,Y波動曲線一致，為同一序列。

 

      由於SBD演演算法計算的是距離，因此在計算距離前我們需要進行Z-score歸一化處理。

      細心的朋友可以發現，當延遲為0時，歸一化後該演演算法中的ncc值相當於在計算皮爾森相關係數。

      SBD演演算法的缺點就是計算量大，在類似KPI場景資料量龐大的時候，SBD演演算法可能無法得到支撐。

      所以，我認為條件允許的情況下，我們可以儘可能地確定好延遲s的數值然後再進行帶入計算。

     

 

   好了，廢話不多說，這裡為大家分享下我寫的演演算法函數：

#SBD距離演演算法
def calcSBDncc(x,y,s):
    assert len(x)==len(y)
    assert isinstance(s,int)
    length_ = len(x)
    pow_x = 0
    pow_y = 0
    for i in range(length_):
        pow_x += math.pow(x[i],2)
        pow_y += math.pow(y[i],2)
    dist_x =math.pow(pow_x,0.5)
    dist_y =math.pow(pow_y,0.5)
    dist_xy = dist_x*dist_y
    ccs = 0
    for j in range(length_-s):
         ccs +=  x[j+s]*y[j]
    ncc = ccs/dist_xy
    return ncc
def calcSBD(x,y,s=None):
    assert len(x)==len(y)
    if  s==None:
        length_ = len(x)
        ncc_list = []
        for s in range(length_-1):
            ncc_list.append(calcSBDncc(x,y,s))
        ncc = max(ncc_list)
        sbd = 1 - ncc
    else:
        ncc = calcSBDncc(x,y,s)
        sbd = 1 - ncc
    return sbd

 

 

第一次寫原創，請多指教。如果有不明白的地方，歡迎有興趣的朋友留言交流！