連續時間復指數訊號解析與Matlab影象直觀展現
連續時間指數訊號
連續時間復指數函數:
x
(
t
)
=
C
e
a
t
x(t)=Ce^{at}
x(t)=Ceat
C
C
C 與
a
a
a 一般為複數
1 連續時間實指數訊號
C C C 與 a a a 都是實數,則 x ( t ) x(t) x(t) 為實指數訊號
(高中知識)
2 連續時間週期復指數訊號
x ( t ) = C e a t a = σ + j ω x(t)=Ce^{at}\\ a=\sigma +j\omega x(t)=Ceata=σ+jω
σ
\sigma
σ 是複數
a
a
a 的實部,
ω
\omega
ω 是複數
a
a
a 的虛部,則根據Euler’s formula(尤拉公式)
e
j
ω
t
=
c
o
s
(
ω
t
)
+
j
s
i
n
(
ω
t
)
e
−
j
ω
t
=
c
o
s
(
ω
t
)
−
j
s
i
n
(
ω
t
)
e^{j\omega t}=cos(\omega t)+jsin(\omega t)\\ e^{-j\omega t}=cos(\omega t)-jsin(\omega t)
ejωt=cos(ωt)+jsin(ωt)e−jωt=cos(ωt)−jsin(ωt)
則可以化為:
x
(
t
)
=
C
e
a
t
=
C
e
(
σ
+
j
ω
)
t
=
C
e
σ
t
e
j
ω
t
=
C
e
σ
t
[
c
o
s
(
ω
t
)
+
j
s
i
n
(
ω
t
)
]
=
C
e
σ
t
c
o
s
(
ω
t
)
+
j
C
e
σ
t
s
i
n
(
ω
t
)
x(t)=Ce^{at}=Ce^{(\sigma +j\omega)t}=Ce^{\sigma t}e^{j\omega t}=Ce^{\sigma t}[cos(\omega t)+jsin(\omega t)]=Ce^{\sigma t}cos(\omega t)+jCe^{\sigma t}sin(\omega t)
x(t)=Ceat=Ce(σ+jω)t=Ceσtejωt=Ceσt[cos(ωt)+jsin(ωt)]=Ceσtcos(ωt)+jCeσtsin(ωt)
此結果表明復指數訊號可以分解為實、虛兩部分,實部包含餘弦訊號,虛部包含正弦訊號
2.1 當 a a a 是純虛數,即 σ = 0 \sigma = 0 σ=0 時
x ( t ) = e j ω 0 t x(t)=e^{j\omega_0t} x(t)=ejω0t
我們知道復指數函數 y = e j ω 0 t y=e^{j\omega_0t} y=ejω0t 在空間中是一個螺旋前進的三維影象,它前進的方向是自變數序列 t t t 增大的方向 ω \omega ω 是旋轉的速度。在右手系中,若令 x x x 軸表示 t t t , y y y 軸表示虛部, z z z 軸表示實部,則從 t t t 的正方向往原點看去可以發現:當 ω > 0 \omega>0 ω>0 時,影象順時針旋轉接近;當 ω < 0 \omega<0 ω<0 時,影象逆時針旋轉接近。
我們使用 M a t l a b Matlab Matlab 繪圖畫出復指數 x ( t ) = e j ω 0 t x(t)=e^{j\omega_0t} x(t)=ejω0t 的圖,以便於我們直觀理解
程式部分在https://blog.csdn.net/ctyqy2015301200079/article/details/83787163的基礎上修改
w = 1; %也可以改成-1
t = 0:0.1:20;
sigma = 0; %這個值為sigma值,後面討論一般復指數函數有用
f=exp((sigma + 1j*w)*t);
L=length(t);
x=t; %以該複函數自變數t作為三維影象的x軸
y=imag(f); %以該複函數虛部作為三維影象的y軸
z=real(f); %以該複函數實部作為三維影象的z軸
y_0=zeros(size(t)); %獲取y=0的點集
y_1=ones(size(t)); %獲取y=1的點集
z_0=zeros(size(t)); %獲取z=0的點集
z_1=ones(size(t)); %獲取z=1的點集
plot3(x,y,z,'.b'); %繪製虛指數函數影象
hold on
grid on
x1=[x;x];
y1=[y;y_0];
z1=[z;z_0];
% 繪製復指數函數影象上的點對應的連線
for i=1:L
plot3(x1(:,i),y1(:,i),z1(:,i),'b');
end
% 繪製副部指數函數影象所繞的軸
plot3(x,y_0,z_0,'k');
% 繪製實部的在底面的投影圖
plot3(x,y,-1*z_1,'.g');
% 繪製實部的點對應的連線
y2=[y;y_0];
z2=[-1*z_1;-1*z_1];
for i=1:L
plot3(x1(:,i),y2(:,i),z2(:,i),'g');
end
% 繪製虛部的在後面的投影圖
plot3(x,y_1,z,'.r');
% 繪製虛部的點對應的連線
y3=[y_1;y_1];
z3=[z;z_0];
for i=1:L
plot3(x1(:,i),y3(:,i),z3(:,i),'r');
end
當 w = 1 w=1 w=1 時:可以得到結果如圖1所示,從 t t t 正方向往原點看去,影象的確順時針靠近
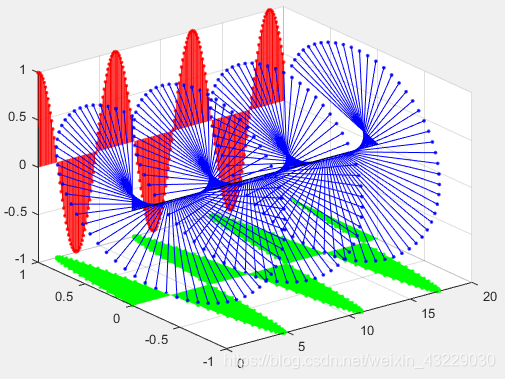
當 w = − 1 w=-1 w=−1時:可以得到結果如圖2所示,從 t t t 正方向往原點看去,影象的確逆時針靠近
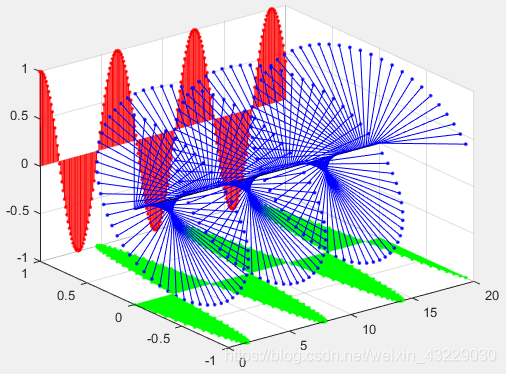
上圖自變數 t t t 變化範圍為 [ 0 , 20 ] [0,20] [0,20] ,紅色為實部,綠色為虛部,複數為藍色,我們可以看到紅色為餘弦函數,綠色為正弦訊號, w w w 的正負改變了虛部的符號,所以我們可以看到當 w w w 變為 − 1 -1 −1 的時候,正弦訊號反相。
我們可以很清楚的看到 x ( t ) = e j ω 0 t x(t)=e^{j\omega_0t} x(t)=ejω0t 是週期訊號,且 e j ω 0 t e^{j\omega_0t} ejω0t 與 e − j ω 0 t e^{-j\omega_0t} e−jω0t 週期相同 。下面我們從數學層面去證明:
如果存在:
e
j
ω
0
t
=
e
j
ω
0
(
t
+
T
)
e^{j\omega_0t}=e^{j\omega_0(t+T)}
ejω0t=ejω0(t+T)
則表示
x
(
t
)
=
e
j
ω
0
t
x(t)=e^{j\omega_0t}
x(t)=ejω0t 是週期訊號,要使
e
j
ω
0
t
=
e
j
ω
0
(
t
+
T
)
e^{j\omega_0t}=e^{j\omega_0(t+T)}
ejω0t=ejω0(t+T)
就必須有:
e
j
ω
0
t
=
e
j
ω
0
(
t
+
T
)
=
e
j
ω
0
t
e
j
ω
0
T
e^{j\omega_0t}=e^{j\omega_0(t+T)}=e^{j\omega_0t}e^{j\omega_0T}
ejω0t=ejω0(t+T)=ejω0tejω0T
則要有
e
j
ω
0
T
=
1
e^{j\omega_0T}=1
ejω0T=1
若
ω
0
=
0
\omega_0=0
ω0=0 ,則
x
(
t
)
=
1
x(t)=1
x(t)=1,這時對於任何
T
T
T 值都是週期性的,若
ω
0
≠
0
\omega_0 ≠ 0
ω0=0,則有:
e
j
ω
0
T
=
c
o
s
(
ω
0
T
)
+
j
s
i
n
(
ω
0
T
)
=
1
e^{j\omega_0T}=cos(\omega_0 T)+jsin(\omega_0 T)=1
ejω0T=cos(ω0T)+jsin(ω0T)=1
則我們知道要使上面式子成立(高中三角函數知識)則最小正
T
T
T 值,即基波週期
T
0
T_0
T0 應該為:
T
0
=
2
π
∣
ω
0
∣
T_0={\frac{2\pi}{|\omega_0|}}
T0=∣ω0∣2π
可見
e
j
ω
0
t
e^{j\omega_0t}
ejω0t 與
e
−
j
ω
0
t
e^{-j\omega_0t}
e−jω0t 週期相同。證畢。
我們可以看到基波週期 T 0 T_0 T0 是與 ∣ ω 0 ∣ |\omega_0| ∣ω0∣ 成反比的,也稱 ω 0 \omega_0 ω0 是基波頻率(fundamental frequency)
則我們可以討論 ω 0 \omega_0 ω0 是如何影響訊號性質的:
ω 0 \omega_0 ω0 與週期成反比,與振盪速率成正比( T = 1 / f T=1/f T=1/f);當 ω 0 = 0 \omega_0=0 ω0=0 時, x ( t ) x(t) x(t) 變為一個常數,如上面討論的,我們可以說振盪速率為 0 0 0 ,振盪週期無窮大
我們計算週期復指數訊號一週期的總能量和平均功率得到總能量為 T 0 T_0 T0,平均功率為 1 1 1 。則我們可以得出在全部時間內積分總能量就是無窮大,平均功率總為 1 1 1 。也就是說週期復指數訊號具有有限平均功率
3 連續時間一般復指數訊號
3.1 當 a a a 不是純虛數,即 σ ≠ 0 \sigma ≠ 0 σ=0 時
由開頭已經推匯出:
x
(
t
)
=
C
e
a
t
=
C
e
σ
t
c
o
s
(
ω
t
)
+
j
C
e
σ
t
s
i
n
(
ω
t
)
x(t)=Ce^{at}=Ce^{\sigma t}cos(\omega t)+jCe^{\sigma t}sin(\omega t)
x(t)=Ceat=Ceσtcos(ωt)+jCeσtsin(ωt)
我們補充將
C
C
C 用極座標表示,
a
a
a 不變用笛卡爾座標來表示,
C
=
∣
C
∣
e
j
θ
a
=
σ
+
j
ω
C=|C|e^{j\theta}\\ a=\sigma +j\omega
C=∣C∣ejθa=σ+jω
則可以進一步展開為:
C
e
a
t
=
∣
C
∣
e
σ
t
c
o
s
(
ω
t
+
θ
)
+
j
∣
C
∣
e
σ
t
s
i
n
(
ω
t
+
θ
)
Ce^{at}=|C|e^{\sigma t}cos(\omega t+\theta)+j|C|e^{\sigma t}sin(\omega t+\theta)
Ceat=∣C∣eσtcos(ωt+θ)+j∣C∣eσtsin(ωt+θ)
則我們可以得出如下結論:
當 σ = 0 \sigma = 0 σ=0 時,實部虛部都是正弦序列(正弦和餘弦統稱正弦訊號)(等幅振盪)
當 σ > 0 \sigma > 0 σ>0 時,實部與虛部是一個振幅呈指數增長的正弦訊號。(增幅振盪)
當 σ < 0 \sigma < 0 σ<0 時,實部與虛部是一個振幅呈指數衰減的正弦訊號。(衰減振盪/阻尼正弦震盪(damped sinusoids))
我們修改上面
M
a
t
l
a
b
Matlab
Matlab 程式碼的 sigma 變數值來觀察。
當 σ = 0.1 > 0 \sigma = 0.1>0 σ=0.1>0 時,可以看到其為增幅震盪:
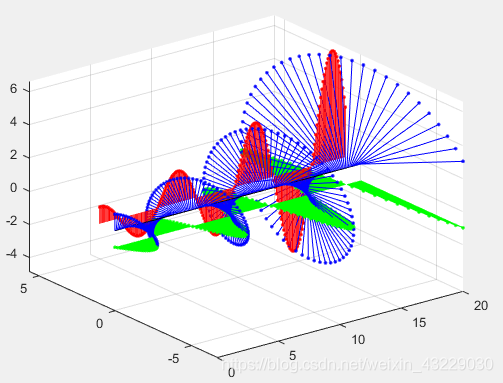
當 σ = − 0.1 < 0 \sigma = -0.1<0 σ=−0.1<0 時,可以看到其為衰減震盪:
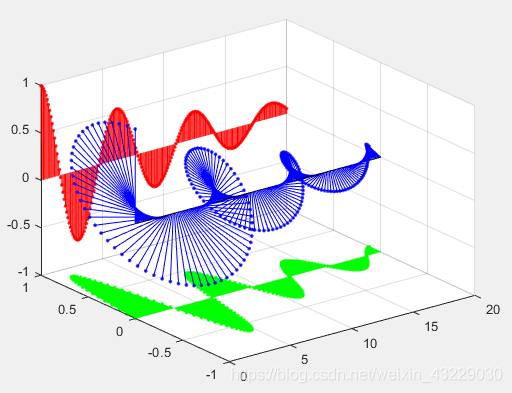
參考 https://blog.csdn.net/lsywyy/article/details/96440059 程式碼
使用另一種方法也可以畫出衰減振盪:
clc
clear
s=-0.1+1j*pi/2;
t=0:0.01:30;
f=exp(s.*t);
x=t;
y=imag(f);
z=real(f);
plot3(x,y,z,'-black');
grid on
hold on
%畫軸
y_0=zeros(size(t)); %獲取y=0的點集
z_0=zeros(size(t)); %獲取z=0的點集
plot3(x,y_0,z_0,'-black');
畫出圖如下所示:
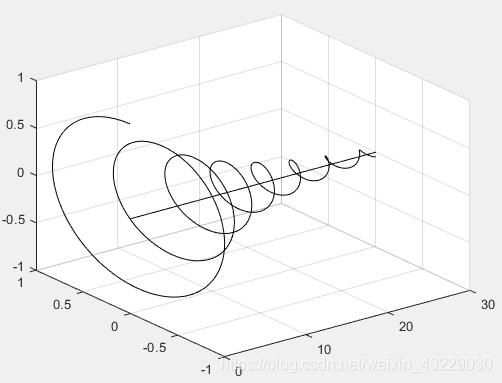
最後 a = σ + j ω a=\sigma +j\omega a=σ+jω 中 σ \sigma σ 與 ω \omega ω 都等於 0 0 0 的時候,變為直流訊號。