前言

前段時間面試百度Java技術崗時碰到了一道演演算法題：任意數分三組，使得每組的和儘量相等。由於時間倉促，加之面試時頭昏腦漲，這道題沒做出來甚至沒有給出思路，導致百度面試之旅失敗。這讓我多少有些遺憾和不甘。因為最近接觸演演算法的東西較多而且本身對演演算法感興趣，所以回家之後絞盡腦汁想把這題做出來。

 

說說我的思路：首先一定要先排序，這也是解決問題的關鍵。然後降序排序後的前三個數各分一組把剩餘數往三個數上疊加。我最開始的思路也是如此，問題在於分組個數不確定，出現極端大的數怎麼辦，怎麼疊加？那層窗戶紙就是將剩餘數中的最大值加到前三個數的最小值上，然後重排序，繼續疊加，直到陣列個數剩三個為止！（不知道大家能不能看懂）我事後解題思路大致就是這樣，太苦逼了。

還記得我當初校招的時候第一場面試也是倒在演演算法，演演算法可以說是我們每個程式設計師的痛，明明平時工作的時候不會太多用到，但這個卻是面試必問的點，也是我們進階必須要面對的東西。現在演演算法挺吃香的，但我們也不可能全身心的投入到演演算法的學習，這時候就需要一本好的參考書來協助我們學習。下面要與大家介紹的檔案可以作為從事計算機研究與開發的技術人員的參考書，特別是對正在準備面試、參加選拔性考試以及校園面試的讀者尤為有用。

這份檔案以Java為描述語言，介紹了計算機程式設計中使用的資料結構和演演算法。這份檔案強調問題及其分析，而非理論闡述，共分為21章，講述了基本概念、遞迴和回溯、連結串列、棧、佇列、樹、優先佇列和隊、並查集DAT、圖演演算法、排序、查詢、選擇演演算法（中位數)、符號表、雜湊、字串演演算法、演演算法設計技術、貪婪演演算法、分治演演算法、動態規劃演演算法、複雜度型別等內容。每章首先闡述必要的理論基礎，然後給出問題集。檔案中大約有700個演演算法問題及相應的解法，對於許多問題，檔案中提供了多個具有不同複雜度的解決方法。由於篇幅限制無法全部展示出來，需要的朋友只需要點贊文章，關注我之後私信【666】即可獲取！

位元組內部演演算法檔案

第1章緒論

本章的目的是闡述演演算法分析的重要性、它們的表示法和關係，並儘可能求解多個問題。首先，讓我們重點關注演演算法的基本要素、分析的重要性，然後再逐步討論上述提及的其他主題。在完成本章的學習後，能夠分析任意給定演演算法的複雜度(特別是遞迴函數)。

 

第2章遞迴和回溯

本章將探討一個重要的內容「遞迴」。本書中幾乎每章都要用到遞迴，同時還介紹一個與之相關的概念「回潮」。

 

第3章連結串列

第4章棧

第5章佇列

第6章樹

第7章優先佇列和堆

第8章並查集ADT

本章將介紹一種非常重要的數學概念;集合。它說明如何表示一組無需考慮順序的元素。並查集ADT可以表示一組無序元素，可用來解決等價問題。並查集易於實現，使用一個簡單陣列就能實現它，且每個函數也只需幾行程式碼。在許多演演算法中，並查集ADT是作為一個輔助資料結構而存在的(例如，圖論中的Kruscal演演算法)。在討論並查集ADT前，首先了解集合的幾個基本性質。

 

第9章圖演演算法

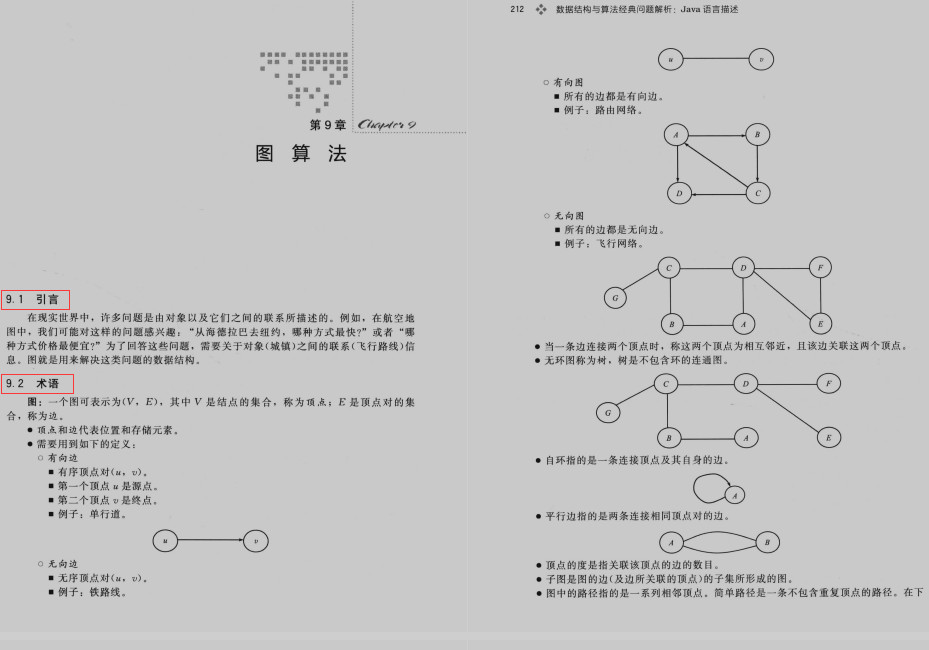
在現實世界中，許多問題是由物件以及它們之間的聯絡所描述的。例如，在航空地圖中，我們可能對這樣的問題感興趣:「從海德拉巴去紐約，哪種方式最快?」或者「哪種方式價格最便宜?」為了回答這些問題，需要關於物件(城鎮)之間的聯絡(飛行路線)資訊。圖就是用來解決這類問題的資料結構。

 

第10章排序

第11章查詢

第12章選擇演演算法(中位數)

第13章符號表

第14章雜湊

第15章字串演演算法

為了理解字串演演算法的重要性，考慮在任意一個瀏覽器(如InternetExplorer、Fire-fox或Google Chrome)中輸入一個URL(Uniform Resource Locator，統一資源定位符)時發生的情況。在鍵入URL的一些字首字元后，可以看見瀏覽器會顯示一個所有可能的URL.列表。這意味著，瀏覽器執行了一些內部處理後，給使用者一個可能匹配的URL列表。這種技術常稱為自動完成。

 

第16章演演算法設計技術

前面的章節針對不同的問題介紹了各種演演算法。在求解一個新問題時，通常的思路是尋找當前問題與已解決問題之間的相似之處，從面輕鬆找到新問題的求解方法。本章將對各種演演算法按照不同的方法進行分類，然後在隨後的3章中分別介紹3個演演算法設計思想〔即貧婪、分治和動態規劃〕.

 

第17章貪婪演演算法

首先通過對一個簡單理論的討論，初步理解貪婪思想。以下棋為例，每一步的決策都需要考慮對後續棋局的影響。而在網球(或排球)比賽中，選手的行為僅取決於當前的狀況，選擇當下最為正確的動作，而不關心後續的影響。這說明在某些情況下選擇當下最佳行為的決策，可以得到一個最優解(貪婪)，但並非所有情況都如此，貪婪策略適用於上述第二類問題。

 

第18章 分治演演算法

對於第17章列舉的許多問題，貪婪策略不能提供最優解。而其中的某些問題可通過分支(Divid and Conquer，D&C)法來輕鬆求解。分治法是一種重要的基於遞迴的演演算法設計技術，分治演演算法遞迴地將問題分解為兩個或多個同型別的子問題，直至這些子問題簡單到能夠直接求解，然後再將這些子同題的解合成為原始問題的解。

 

第19章動態規劃演演算法

本章將試圖求解那些採用其他技術(如分治法和貪婪法)無法獲得最優解的問題。動態規劃(Dynamic Programming，DP)是一項雖簡單但較難掌握的技術。一個容易識別和求解DP問題的方法是通過求解儘可能多的問題。「Programming」一詞並不是指程式設計，二是表示填充表格(類似於線性規劃）

 

第20章複雜度型別

在前面的各章中，描述了不同問題求解的複雜度。某些演演算法隨著問題規模的增加其複雜度的增長速率較低，而另一些則有比較高的增長速率。對於具有較低增長率的問題，稱為簡單問題(或易求解問題);對於具有較高複雜度的問題，稱為難問題(或難求解問題)。該分類是基於求解某個問題時演演算法的執行時間(或者佔用記憶體)決定的。

 

第21章雜談

本章將介紹一些對於面試和考試有用的話題，我們來看看文中的一些其他的程式設計題。

 

• 設計一個演演算法，按照螺旋順序依次輸出矩陣中的元素。
• 設計一個洗牌演演算法。
• 基於反轉演演算法的陣列旋轉問題。設計一個函數rotate(A[]，d，n)，該函數將大小為n的陣列旋轉d個元素。例如，陣列1，2，3，4，5，6，7在經過2個元素的旋轉後變為3，4，5，6，7，1，2。
• 已知陣列s[1..n]和反轉函數(s，i，j)，反轉函數顛倒à到j之間的陣列元素(包括第i和j個元素）的順序。以下序列的功能是什麼?（1<kn)
• 字串由詞和空格組成，設計一個程式將字串中所有空格移到字串的最前面，要求僅遍歷陣列一次，並且在原字串中進行調整。
• 能否降低問題5演演算法的複雜度?
• 對於一個包含詞和空格的字串，設計一個程式將所有空格移到字串的末尾，要求僅遍歷陣列一次，並且在原字串中進行調整。
• 移動0到末尾。給定由n個整陣列成的陣列，將陣列中的0移動到末尾。例如，如果有陣列{1，9，8，4，0，0，2，7，0，6，0}，應該變為{1，9，8，4，2，7,6，0，0，0}。所有其他元素的順序不變。
• 能否降低問題8演演算法的複雜度?
• 問題9的變型。已知一個包含正數和負數的陣列，設計一個演演算法將正數和負數分開，要求正數和負數的相對順序保持不變。輸人:一5，3，2，一l，4，一8，輸出:一5，—1，—8，3，4，2。

這些問題你能答出多少？（手動狗頭）反正我一時半會搞不定。不過沒關係檔案中也是有著每一題的解析，最後我們來看一看一位大佬對演演算法的一些看法。

大佬的一些看法

PS：我國軟體學習形式主義太過嚴重，演演算法這種東西必須要與實踐相結合才能真正起到作用，很多程式設計師演演算法非常厲害可是就是做不出東西，為啥，因為他們並不能能深刻理解演演算法，很多情況就是機械性套用演演算法，而且演演算法這種東西必須要與程式設計技術相結合，單一的演演算法幾乎難以解決問題，比如雲端計算就屬於演演算法，與網際網路技術，多執行緒技術，多程序技術，和各種軟硬體技術結合體，單一從一個層面去看演演算法幾乎解決不了任何問題，國外的頂級軟體大師則是將演演算法轉化為計算機可以識別演演算法，並結合於其他計算機技術，使其達到最大效能，例如深度學習就和cuda相結合，使其最好的運轉在某些硬體之上，再加之cuda具有極強並行運算能力，其效能達到最大化，其實演演算法與計算機技術具有極大跨度需要那種對數學或其他學科與計算機都較為精通的人才能正真轉化，否則單—演演算法工程也僅僅只是書呆子的形式。難成大事。

我覺得他字多他說的都對，言歸正傳如果有朋友需要這份位元組內部演演算法檔案，只需要點贊文章，關注我之後私信【666】即可免費獲取了~