【博弈論&&建模】 Candy Piles
題目描述:

S o l u t i o n Solution Solution
我們形象的理解一下去糖果的過程是怎麼樣的。
首先,我們將原本無序的糖果排序一下變成有序的序列,這樣子能夠較好的處理取出石子最多這一操作,如下:
//這裡借用一下atcoder的官方圖片,以助於理解
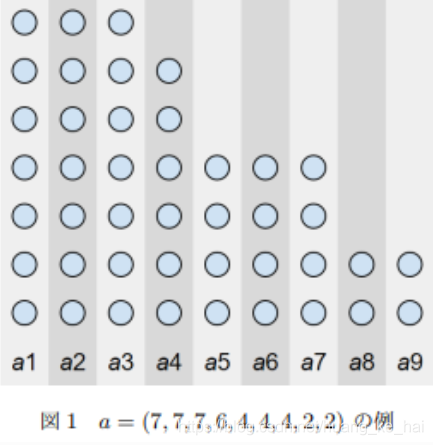
然後我們模擬一下取糖果的效果。
如果是取走石子最多的一堆,實際上相當於消除最左邊的一列:

如果是給每堆石子都取走一個,那麼就是消除最下面的一行:
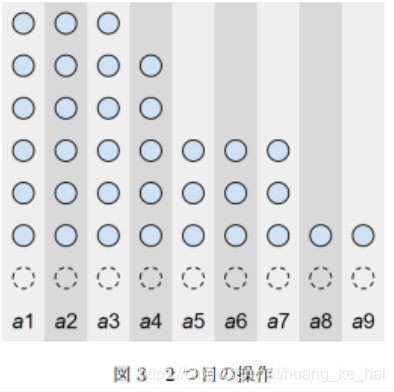
因此,我們將這樣的操作形象理解之後可以發現,這樣的操作要麼是消除最左邊的一列要麼是消除最底下的一行。
接著我們抽象的將這樣的情況轉化為網格圖:
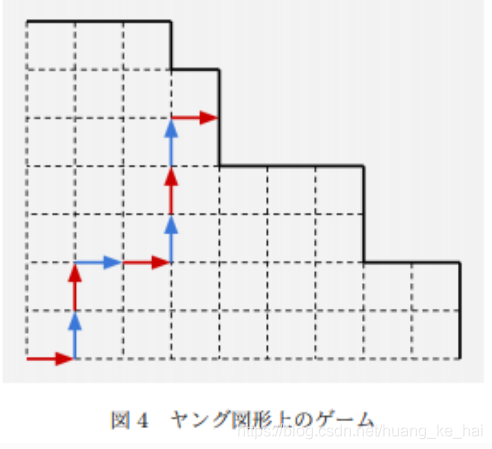
將操作轉化到網格圖上,不難想到,消除最右邊的一列,就是往右走一格;消除最下面的一行,就是往上走一格。
什麼情況結束呢?走到邊界就結束了,並且誰走到邊界誰就輸。
OK,我們重新回到題目上,題目上求的是是否必勝與必敗,這是一道博弈。
我們給每個點都附上一個身份:必勝點與必敗點。表示走到當前是必勝還是必敗。
顯然的,網格圖的邊界都是必敗點。而對於一個點,只要他的右邊或者上面有一個點是必敗點,那麼當前就是必勝點。如果他的右邊以及上面都是必勝點,那麼當前就是必敗點。
這裡用○表示必敗點,×表示必勝點:
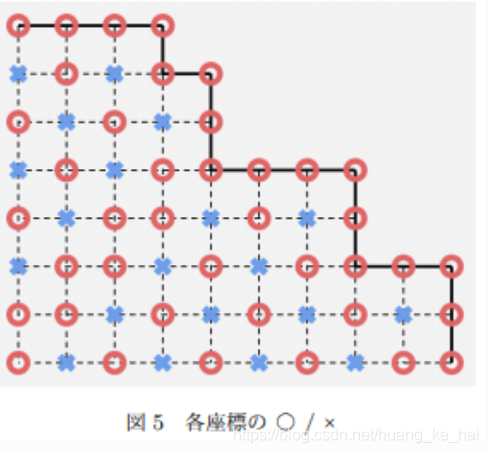
我們是從原點 ( 0 , 0 ) (0,0) (0,0)出發,下一步是先手。所以可以理解為後手此時處在原點。那麼當原點是必勝點是,後手必勝,原點是必敗點時,先手必勝。
但是,對於此題的資料範圍而言,我們顯然不能夠將整個網格圖的資訊都記錄下來。所以我們需要在上圖的基礎上尋找規律:

我們發現,除了邊界點,每一條對角線上的點都是相同型別的。
因此,我們如果想要確定原點的型別是怎麼樣的,只要確定其對角線上的點的型別是怎麼樣的即可。
原點斜向上的對角線是45度對角線,所以我們是需要找到以原點左下角的最大正方形,設右上角為
(
i
,
i
)
(i,i)
(i,i):
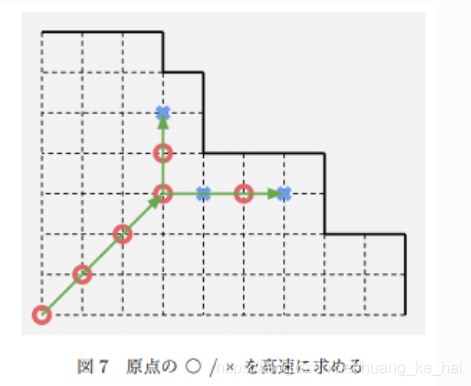
如果當前
(
i
,
i
)
(i,i)
(i,i)到邊界的一端的前一個點的距離為奇數,那麼當前點就是必敗點,即原點是必敗點;反之原點就是必勝點。
到此,這道題就結束了!
十分巧妙的建模……
Code
??那麼簡單還不會寫??