一、演演算法目錄合集

1.地址

   演演算法目錄合集

2.說明

  該地址指向所有由本人自己所經歷的演演算法習題(也有可能僅僅是一個入門的案例或者是經典案例)，僅僅為我做過而且比較有意思的，也許還會有一些我自己想出來的，出於興趣寫在這裡,具體格式我會在下面列明，總目錄也會在這裡出現，方便查閱以及自己進行復習回顧。

二、題目說明

1.題幹

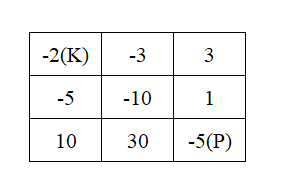
  一些惡魔抓住了公主（P）並將她關在了地下城的右下角。地下城是由 M x N 個房間組成的二維網格。我們英勇的騎士（K）最初被安置在左上角的房間裡，他必須穿過地下城並通過對抗惡魔來拯救公主。

  騎士的初始健康點數為一個正整數。如果他的健康點數在某一時刻降至 0 或以下，他會立即死亡。

  有些房間由惡魔守衛，因此騎士在進入這些房間時會失去健康點數（若房間裡的值為負整數，則表示騎士將損失健康點數）；其他房間要麼是空的（房間裡的值為 0），要麼包含增加騎士健康點數的魔法球（若房間裡的值為正整數，則表示騎士將增加健康點數）。

  為了儘快到達公主，騎士決定每次只向右或向下移動一步。

  編寫一個函數來計算確保騎士能夠拯救到公主所需的最低初始健康點數。

  例如，考慮到如下佈局的地下城，如果騎士遵循最佳路徑 右 -> 右 -> 下 -> 下，則騎士的初始健康點數至少為 7。

  說明:

• 騎士的健康點數沒有上限。
• 任何房間都可能對騎士的健康點數造成威脅，也可能增加騎士的健康點數，包括騎士進入的左上角房間以及公主被監禁的右下角房間。

2.原地址

  174. 地下城遊戲

三、實現步驟

1.思路分析

1.1.分析問題

  對於這個題,有一種常規的方法——動態分析（一看這不就是動態分析😀），因為血量是由兩個條件決定的（每個房間不能死掉，並且到終點時血量最少），所以正著去分析時有難度，不如講血量定為1，反向分析，也就是說：當我們到達座標$(i,j)$時，如果此時我們的路徑和不小於 $dp[i][j]$ ，我們就能到達終點。 既然要反向分析了，那我就不展示動態分析了，動態分析官方題解也有，我就用一個一提反向就能想起來的詞兒去做：遞迴。沒錯，我已經在前幾篇文章講過遞迴的一些題了，這其實也可以遞迴求解。

  首先要分析一下，如何遞迴？
  關注一下上面一段的黃線，就假設前面已經操作完了，那麼現在我們只需要選取向右或者向下，取一個$min$就可以了，直接呼叫$Math.min()$方法就行了，如果這時候我們的現存血量減去本格子的耗血量（負值也適用）大於零，就說明或者，那麼便可以讓血量變成1（既然多少血都能或者，那麼1可以使血量保持最低），如果小於零，說明之前的血量不夠用，那麼剩餘血量必須得是最小值$min$減去本格的耗血量。

  就這樣一直遞迴回第一步，返回即可。

1.2.具體步驟

① 特殊情況分析

  如果遇到了邊界，則返回int的最大值過濾，之所以不寫999或者9999，是因為你也不知道一個格子究竟扣多少血，萬一給你來個幾萬呢😄所以來個Integer.MAX_VALUE穩妥一些。

if (m >= dungeon.length || n >= dungeon[0].length) {
	return Integer.MAX_VALUE;
}

  如果找到了公主，則返回所就到公主之前的時候的血量最小值，把值返回，以供呼叫者使用。

if (m == dungeon.length - 1 && n == dungeon[0].length - 1) {
	return dungeon[m][n] >= 0 ? 1 : 1 - dungeon[m][n];
}

  如果本位置為0，說明dp還沒有被賦值，此項判斷是為了把指標放在公主的位置，並往回尋找。

if (dp[m][n] != 0) {
	return dp[m][n];
}

② 常規分析

  常規步驟就是比較簡單的了，選取兩種分支的最小值，並將其與本格子的耗血量進行比較，來為dp陣列賦值儲存，最終返回$dp[0][0]$即可。

int min = Math.min(blood(dp,dungeon, m + 1, n), blood(dp,dungeon, m, n + 1));
dp[m][n] = dungeon[m][n] - min >= 0 ? 1 : min - dungeon[m][n];
return dp[m][n];

2.程式碼實現

2.1 方法程式碼

public class Solution174 {
    public int calculateMinimumHP(int[][] dungeon) {
        int[][] dp = new int[dungeon.length][dungeon[0].length];
        return blood(dp, dungeon, 0, 0);
    }

    public int blood(int[][] dp, int[][] dungeon, int m, int n) {
        if (m >= dungeon.length || n >= dungeon[0].length) {
            return Integer.MAX_VALUE;
        }
        if (m == dungeon.length - 1 && n == dungeon[0].length - 1) {
            return dungeon[m][n] >= 0 ? 1 : 1 - dungeon[m][n];
        }
        if (dp[m][n] != 0) {
            return dp[m][n];
        }
        int min = Math.min(blood(dp,dungeon, m + 1, n), blood(dp,dungeon, m, n + 1));
        dp[m][n] = dungeon[m][n] - min >= 0 ? 1 : min - dungeon[m][n];
        return dp[m][n];
    }
}

2.2 測試部分程式碼

  這裡隨便定義一個隨便看看就好了

public class Test174Hard {
    public static void main(String[] args) {
        Solution174 s = new Solution174();
        int i1 = s.calculateMinimumHP(new int[][]{{1, 2, 3}, {0, -5, 0}, {-2, 1, 1}});
        int i2 = s.calculateMinimumHP(new int[][]{{-2,-3,3},{-5,-10,1},{10,30,-5}});
        System.out.println(i1);
        System.out.println(i2);
    }
}

  測試結果

1
7

2.3 耗用資源情況

四、官方題解

1.原地址

力扣官方答疑戳這裡

2.方法一——動態規劃

思路分析

思路及演演算法
  幾個要素：「$M\times N$ 的網格」「每次只能向右或者向下移動一步」。讓人很容易想到該題使用動態規劃的方法。
  但是我們發現，如果按照從左上往右下的順序進行動態規劃，對於每一條路徑，我們需要同時記錄兩個值。第一個是「從出發點到當前點的路徑和」，第二個是「從出發點到當前點所需的最小初始值」。而這兩個值的重要程度相同，參看下面的範例：

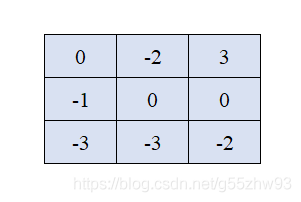
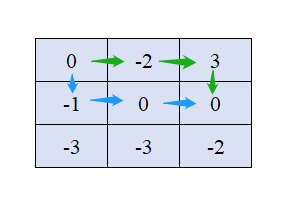
  從$(0,0)$到$(1,2)$ 有多條路徑，我們取其中最有代表性的兩條：

• 綠色路徑「從出發點到當前點的路徑和」為 $1$，「從出發點到當前點所需的最小初始值」為 $3$。
• 藍色路徑「從出發點到當前點的路徑和」為 $-1$，「從出發點到當前點所需的最小初始值」為 $2$。

  
  我們希望「從出發點到當前點的路徑和」儘可能大，而「從出發點到當前點所需的最小初始值」儘可能小。這兩條路徑各有優劣。
  在上圖中，我們知道應該選取綠色路徑，因為藍色路徑的路徑和太小，使得藍色路徑需要增大初始值到 $4$ 才能走到終點，而綠色路徑只要 $3$ 點初始值就可以直接走到終點。但是如果把終點的$-2$ 換為 $0$，藍色路徑只需要初始值 $2$，綠色路徑仍然需要初始值 $3$，最優決策就變成藍色路徑了。
  因此，如果按照從左上往右下的順序進行動態規劃，我們無法直接確定到達 $(1,2)$ 的方案，因為有兩個重要程度相同的引數同時影響後續的決策。也就是說，這樣的動態規劃是不滿足「無後效性」的。
  於是我們考慮從右下往左上進行動態規劃。令 $dp[i][j]$ 表示從座標$(i,j)$ 到終點所需的最小初始值。換句話說，當我們到達座標$(i,j)$時，如果此時我們的路徑和不小於 $dp[i][j]$ ，我們就能到達終點。
  這樣一來，我們就無需擔心路徑和的問題，只需要關注最小初始值。對於 $dp[i][j]$ ，我們只要關心 $dp[i][j+1]$ 和 $dp[i+1][j]$ 的最小值$minn$。記當前格子的值為$dungeon(i,j)$，那麼在座標 $(i,j)$ 的初始值只要達到$minn-dungeon(i,j)$ 即可。同時，初始值還必須大於等於 $1$。這樣我們就可以得到狀態轉移方程：
  
$$dp[i][j]=max(min(dp[i+1][j],dp[i][j+1])-dungeon(i,j),1)$$
  最終答案即為 $dp[0][0]$。
  邊界條件為，當 $i=n-1$ 或者$j=m-1$ 時，$dp[i][j]$ 轉移需要用到的$dp[i][j+1]$ 和 $dp[i+1][j]$ 中有無效值，因此程式碼實現中給無效值賦值為極大值。特別地，$dp[n-1][m-1]$ 轉移需要用到的 $dp[n-1][m]$ 和 $dp[n][m-1]$ 均為無效值，因此我們給這兩個值賦值為 $1$。

程式碼實現（Java）

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        int n = dungeon.length, m = dungeon[0].length;
        int[][] dp = new int[n + 1][m + 1];
        for (int i = 0; i <= n; ++i) {
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        dp[n][m - 1] = dp[n - 1][m] = 1;
        for (int i = n - 1; i >= 0; --i) {
            for (int j = m - 1; j >= 0; --j) {
                int minn = Math.min(dp[i + 1][j], dp[i][j + 1]);
                dp[i][j] = Math.max(minn - dungeon[i][j], 1);
            }
        }
        return dp[0][0];
    }
}

複雜度

• 時間複雜度：
     $O(N\times M)$，其中$N$，$M$ 為給定矩陣的長寬。
• 空間複雜度：
    $O(N\times M)$，其中$N$,$M$ 為給定矩陣的長寬，注意這裡可以利用捲動陣列進行優化，優化後空間複雜度可以達到 $O(N)$。