迴歸模型彙總、評估和總結
迴歸模型彙總、評估和總結
在本篇您將學到:
● 迴歸類任務的基本解決方法
● 針對任務資料集的特徵工程
● 迴歸模型的使用和調參
● 基礎模型與樹模型的實驗對比分析
本篇包含的迴歸模型有
LinearRegression:線性迴歸模型、
Ridge:嶺迴歸模型 、
Lasso:Lasso迴歸模型 、
ElasticNet:彈性網路迴歸,嶺迴歸和Lasso迴歸的混合模型、
SVR:支援向量迴歸 、
GradientBoostingRegressor:GB梯度提升迴歸模型
XGBoost、LightGBM、CatBoost、NGBoost:四大樹的迴歸模型
迴歸模型目錄
I 庫
在一般的Anaconda環境下,還需要pip安裝如下兩個包:
mlxtend:堆疊迴歸模型
ngboost:斯坦福吳恩達團隊提出NGBoost:用於概率預測的自然梯度提升,這個模型除了慢了點,在與xgboost、lightgbm、catboost三大經典樹模型比較下,其迴歸效果最好。
pip install mlxtend -i https://pypi.douban.com/simple
pip install ngboost -i https://pypi.tuna.tsinghua.edu.cn/simple
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
from scipy.special import boxcox1p
from scipy.stats import skew,boxcox_normmax
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error,mean_squared_error,explained_variance_score,median_absolute_error,r2_score
from sklearn.preprocessing import MinMaxScaler,StandardScaler,RobustScaler
from sklearn.svm import SVR
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.linear_model import LinearRegression,RidgeCV,LassoCV,ElasticNetCV
from mlxtend.regressor import StackingCVRegressor # pip install mlxtend -i https://pypi.douban.com/simple
from lightgbm import LGBMRegressor
from xgboost import XGBRegressor
from catboost import CatBoostRegressor
from ngboost import NGBRegressor
from ngboost.ngboost import NGBoost # pip install ngboost -i https://pypi.tuna.tsinghua.edu.cn/simple
from ngboost.learners import default_tree_learner
from ngboost.distns import Normal
II 資料
data = pd.read_csv('../data/train.csv')
print('預設值:',data.isna().sum().sum())
data.head()
為保證隱私安全,具體資料不再透漏,大家在實驗或比賽時僅需使用自己的迴歸資料即可
劃分資料集為訓練集和測試集
train_x, test_x, train_y, test_y = train_test_split(X, Y, test_size=0.25,random_state=2020)
III 預設引數
3.1 匯入各類迴歸模型
lr = LinearRegression()
ridge = Ridge()
lasso = Lasso()
enet = ElasticNet()
xgb = XGBRegressor()
lgb = LGBMRegressor()
cat = CatBoostRegressor()
ngb = NGBRegressor()
3.2 模型訓練
lr.fit(train_x,train_y)
ridge.fit(train_x,train_y)
lasso.fit(train_x,train_y)
enet.fit(train_x,train_y)
xgb.fit(train_x,train_y,verbose=False)
lgb.fit(train_x,train_y,verbose=False)
cat.fit(train_x,train_y,verbose=False)
ngb.fit(train_x,train_y)
3.3 模型預測
lr_pre = lr.predict(test_x)
ridge_pre = ridge.predict(test_x)
lasso_pre = lasso.predict(test_x)
enet_pre = enet.predict(test_x)
xgb_pre = xgb.predict(test_x)
lgb_pre = lgb.predict(test_x)
cat_pre = cat.predict(test_x)
ngb_pre = ngb.predict(test_x)
3.4 模型評估
# MAE 平均絕對值誤差
## 用於評估預測結果和真實資料集的接近程度的程度,其其值越小說明擬合效果越好
# MSE 均方差
## 該指標計算的是擬合資料和原始資料對應樣本點的誤差的平方和的均值,其值越小說明擬合效果越好。
# MedianAE 中值絕對誤差
## 此種方法非常適應含有離群點的資料集,越小越好
# EVS 可釋方差得分
## 解釋迴歸模型的方差得分,其值取值範圍是[0,1],越接近於1說明自變數越能解釋因變數的方差變化,值越小則說明效果越差。
# R2 決定係數(擬合優度)
## 判定係數,其含義是也是解釋迴歸模型的方差得分,其值取值範圍是[0,1],越接近於1說明自變數越能解釋因變數的方差變化,值越小則說明效果越差。
mae = []
mse = []
median_ae = []
evs = []
r2 = []
all_less = []
all_more = []
for pre,name in zip([lr_pre,ridge_pre,lasso_pre,enet_pre,xgb_pre,lgb_pre,cat_pre,ngb_pre],
['lr','ridge','lasso','enet','xgb','lgb','cat','ngb']):
print(name,':')
MAE = mean_absolute_error(test_y,pre)
MSE = mean_squared_error(test_y,pre)
EVS = explained_variance_score(test_y,pre)
Median_AE = median_absolute_error(test_y,pre)
R2 = r2_score(test_y,pre)
mae.append(MAE)
mse.append(MSE)
evs.append(EVS)
median_ae.append(Median_AE)
r2.append(R2)
print('\t平均絕對值誤差\t{}\n\t均方差 \t\t{}\n\t中值絕對誤差 \t{}\n\t可釋方差得分 \t{}\n\t決定係數 \t{}'.format(
MAE,MSE,Median_AE,EVS,R2))


資料是冷漠的,還是讓我們來看一下對比圖
y_plot = mae
x_name = ['lr','ridge','lasso','enet','xgb','lgb','cat','ngb']
plt.figure(figsize=(15,10), dpi=80)
plt.subplot(221)
plt.ylim(0.014,0.016)
plt.title('平均絕對值誤差 MAE')
plt.bar(x_name,y_plot)
y_plot = mse
plt.subplot(222)
# plt.ylim(0.014,0.016)
plt.title('均方差 MSE')
plt.bar(x_name,y_plot)
y_plot = median_ae
plt.subplot(223)
# plt.ylim(0.014,0.016)
plt.title('中值絕對誤差 Median_AE')
plt.bar(x_name,y_plot)
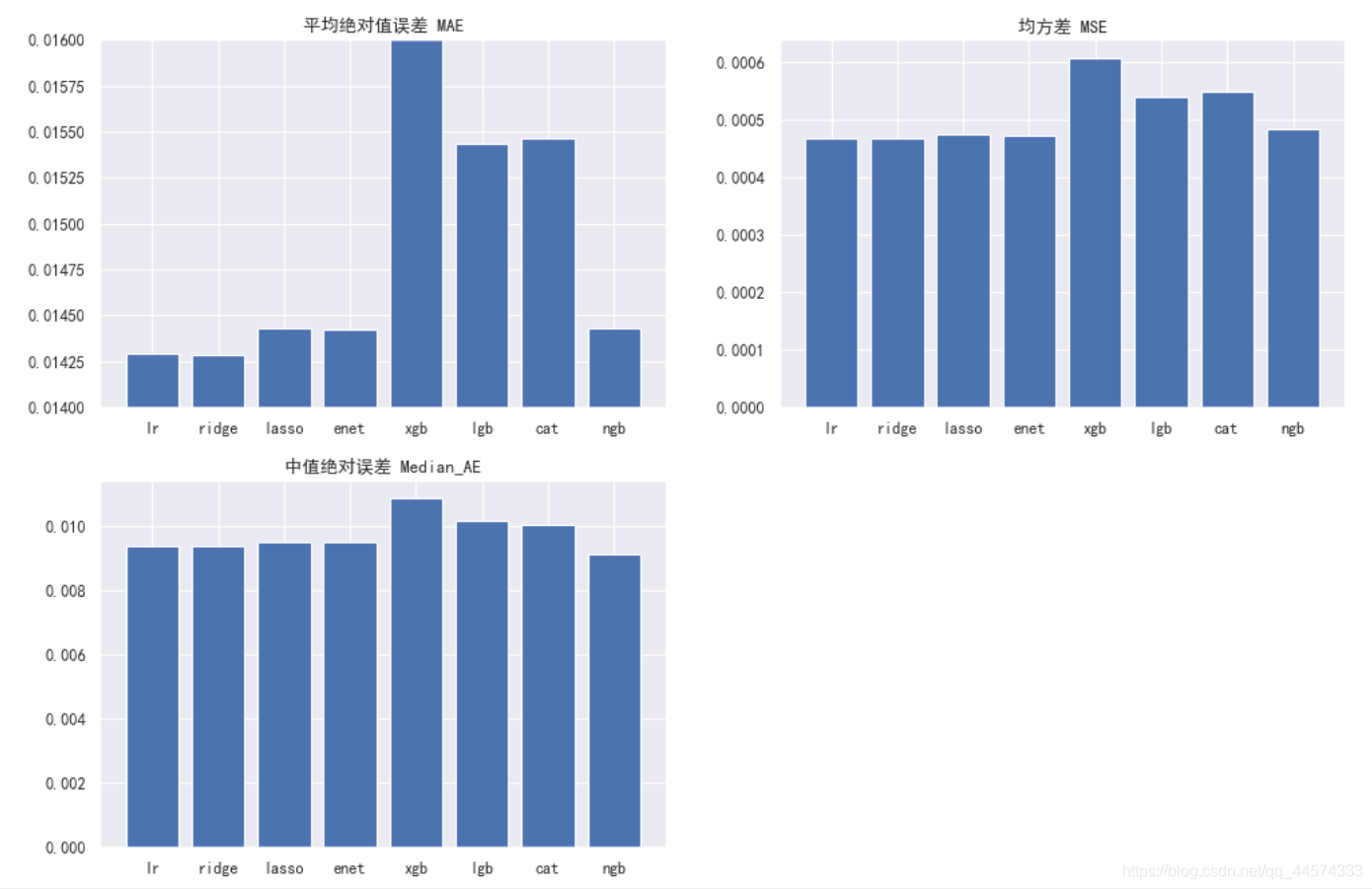
3.5 結論
在預設引數、無任何特徵工程的情況下,可以看出各回歸模型的效果:
ridge >= lr > enet > lasso > ngb > lgb > cat > xgb
有趣的是,我們的基礎模型在這種樸素的情況下效果都不錯,而三大經典樹模型 xgb、lgb、cat的迴歸效果卻較差,但值得一提的是NGBoost還是有著與基礎模型中的enet、lasso一樣不錯的效果的。
IV 特徵工程
對於這份資料,因為其資料均為數值特徵,故筆者在此僅考慮了一種對數值特徵有普適性通用的特徵工程,資料規範化,但規範化又有很多種,在此,我們考慮兩種常見的規範化:
- MinMaxScaler: 歸一到 [ 0,1 ]
- StandardScaler: 通過刪除平均值和縮放到單位方差來標準化特徵
同樣通過模型迴歸效果來決定該選擇哪一種
def choose_scaler(model_name,X):
"""
model_name = ['lr','ridge','xgb','lgb']
return MAE 和 圖
"""
min_max_scaler = MinMaxScaler().fit(X)
standard_scaler = StandardScaler().fit(X)
X_minmax = min_max_scaler.transform(X)
X_standard = standard_scaler.transform(X)
if model_name == 'lr':
print('(MAE) LR:\t0.014288303965603513')
train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
lr.fit(train_x,train_y)
minmax = mean_absolute_error(test_y,lr.predict(test_x))
print('MinMax規範化: ',minmax)
train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
lr.fit(train_x,train_y)
standard = mean_absolute_error(test_y,lr.predict(test_x))
print('Standard規範化:',standard)
plt.bar(['LR','MinMax規範化','Standard規範化:'],[0.014288303965603513,minmax,standard])
elif model_name == 'xgb':
print('(MAE) XGB:\t0.016564375395988443')
train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
xgb.fit(train_x,train_y,verbose=False)
minmax = mean_absolute_error(test_y,xgb.predict(test_x))
print('MinMax規範化: ',minmax)
train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
xgb.fit(train_x,train_y,verbose=False)
standard = mean_absolute_error(test_y,xgb.predict(test_x))
print('Standard規範化:',standard)
plt.bar(['XGB','MinMax規範化','Standard規範化:'],[0.016564375395988443,minmax,standard])
elif model_name == 'ridge':
print('(MAE) Ridge:\t0.0142876509355531')
train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
ridge.fit(train_x,train_y)
minmax = mean_absolute_error(test_y,ridge.predict(test_x))
print('MinMax規範化: ',minmax)
train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
ridge.fit(train_x,train_y)
standard = mean_absolute_error(test_y,ridge.predict(test_x))
print('Standard規範化:',standard)
plt.bar(['Ridge','MinMax規範化','Standard規範化:'],[0.0142876509355531,minmax,standard])
elif model_name == 'lgb':
print('(MAE) LGB:\t0.015437267376697029')
train_x, test_x, train_y, test_y = train_test_split(X_minmax, Y, test_size=0.25,random_state=2020)
lgb.fit(train_x,train_y,verbose=False)
minmax = mean_absolute_error(test_y,lgb.predict(test_x))
print('MinMax規範化: ',minmax)
train_x, test_x, train_y, test_y = train_test_split(X_standard, Y, test_size=0.25,random_state=2020)
lgb.fit(train_x,train_y,verbose=False)
standard = mean_absolute_error(test_y,lgb.predict(test_x))
print('Standard規範化:',standard)
plt.bar(['LGB','MinMax規範化','Standard規範化:'],[0.015437267376697029,minmax,standard])
if minmax<standard:print('選擇MinMax規範化')
else:print('選擇Standard規範化')
4.1 基礎模型lr
先看我們的基礎模型lr對兩種規範化的選擇
choose_scaler('lr',X)
# Standard規範化
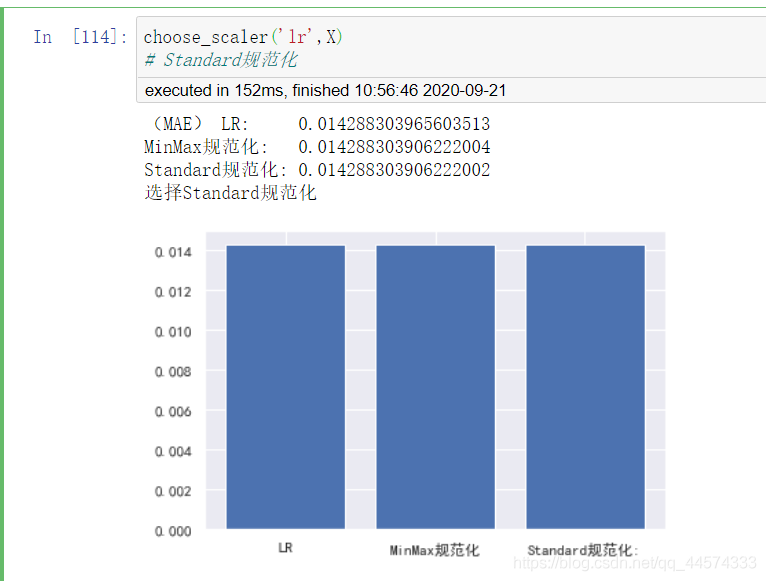
對於lr而言,兩者效果類似,且都比不做規範化效果好。差別不大,但Standard的模型效果更好。
lr選擇StandardScaler。
4.2 基礎模型ridge
choose_scaler('ridge',X)
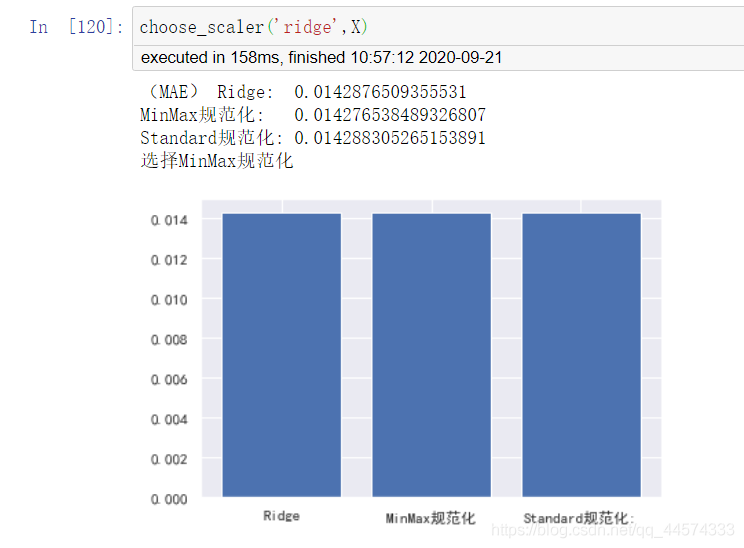
對於ridge而言,兩者效果還是有一定差異的,且Standard後模型效果反而變差了一點。
ridge選擇MinMaxScaler。
4.3 樹模型XGBoost
再讓我們看看樹模型對於倆種規範化的選擇
choose_scaler('xgb',X)
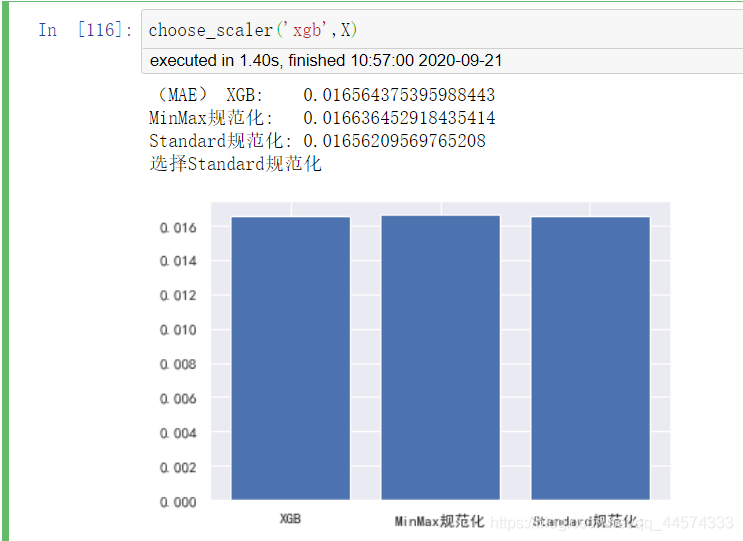
對於樹模型xgb而言,MinMax後模型效果變差,但Standard後模型效果反而變好。和線性模型相比這個實驗結果正好相反,這還是很有趣的。
xgb選擇StandardScaler。
4.4 樹模型Lightgbm
choose_scaler('lgb',X)
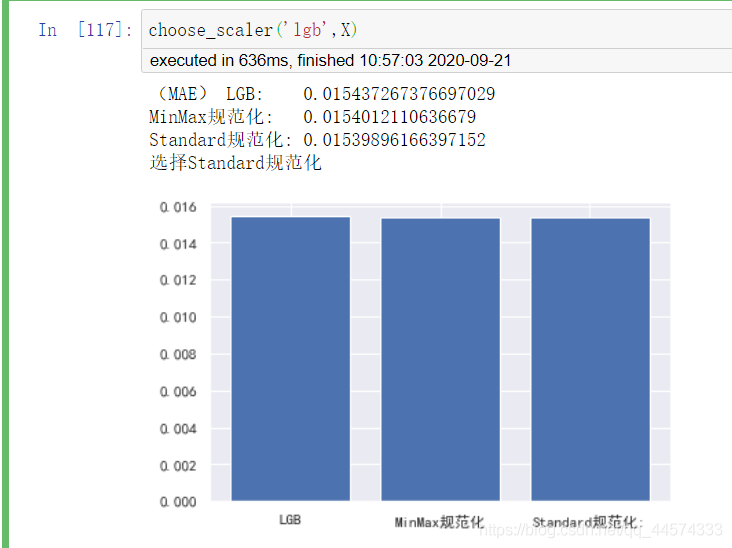
同樣對於樹模型lgb也選擇StandardScaler。
綜上,筆者最終選擇了StandardScaler來規範化資料。
X_standard = pd.DataFrame(standard_scaler.transform(X),columns=X.columns)
V 調參模型
5.1 模型的定義、調參
各種迴歸模型的定義、調參請參見程式碼
#定義LR迴歸模型
# LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
# fit_intercept:是否有截據,如果沒有則直線過原點;
# normalize:是否將資料歸一化;
# copy_X:預設為True,當為True時,X會被copied,否則X將會被覆寫;
# n_jobs:預設值為1。計算時使用的核數
# 無調參
lr = LinearRegression()
#定義ridge嶺迴歸模型(使用二範數作為正則化項。不論是使用一範數還是二範數,正則化項的引入均是為了降低過擬合風險。)
#注:正則化項如果使用二範數,那麼對於任何需要尋優的引數值,在尋優終止時,它都無法將某些引數值變為嚴格的0,儘管某些引數估計值變得非常小以至於可以忽略。即使用二範數會保留變數的所有資訊,不會進行類似PCA的變數凸顯。
#注:正則化項如果使用一範數,它比L2範數更易於獲得「稀疏(sparse)」解,即它的求解結果會有更多的零分量。
alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5]
alphas2 = [5e-05, 0.0001, 0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007, 0.0008]
e_alphas = [0.0001, 0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007]
e_l1ratio = [0.8, 0.85, 0.9, 0.95, 0.99, 1]
ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt))
#定義LASSO收縮模型(使用L1範數作為正則化項)(由於對目標函數的求解結果中將得到很多的零分量,它也被稱為收縮模型。)
#注:正則化項如果使用二範數,那麼對於任何需要尋優的引數值,在尋優終止時,它都無法將某些引數值變為嚴格的0,儘管某些引數估計值變得非常小以至於可以忽略。即使用二範數會保留變數的所有資訊,不會進行類似PCA的變數凸顯。
#注:正則化項如果使用一範數,它比L2範數更易於獲得「稀疏(sparse)」解,即它的求解結果會有更多的零分量。
lasso = make_pipeline(RobustScaler(), LassoCV(max_iter=1e7, alphas=alphas2, random_state=42))
#定義elastic net彈性網路模型(彈性網路實際上是結合了嶺迴歸和lasso的特點,同時使用了L1和L2作為正則化項。)
enet = make_pipeline(RobustScaler(), ElasticNetCV(max_iter=1e7, alphas=e_alphas, l1_ratio=e_l1ratio))
#定義SVM支援向量機模型
svr = make_pipeline(RobustScaler(), SVR(C= 20, epsilon= 0.008, gamma=0.0003,))
#定義GB梯度提升模型(展開到一階導數)
gbr = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.05, max_depth=4, max_features='sqrt', min_samples_leaf=15, min_samples_split=10, loss='huber', random_state =42)
#定義lightgbm模型
lgb= LGBMRegressor(objective='regression',
num_leaves=4,
learning_rate=0.01,
n_estimators=5000,
max_bin=200,
bagging_fraction=0.75,
bagging_freq=5,
bagging_seed=7,
feature_fraction=0.2,
feature_fraction_seed=7,
verbose=-1,
#min_data_in_leaf=2,
#min_sum_hessian_in_leaf=11
)
#定義xgboost模型(展開到二階導數)
xgb = XGBRegressor(learning_rate=0.01, n_estimators=3460,
max_depth=3, min_child_weight=0,
gamma=0, subsample=0.7,
colsample_bytree=0.7,
# objective='reg:linear', nthread=-1,
objective='reg:squarederror', nthread=-1,
scale_pos_weight=1, seed=27,
reg_alpha=0.00006)
#定義catboost模型
cat = CatBoostRegressor(iterations=700,learning_rate=0.02,
depth=12,eval_metric='MAE',random_seed = 23,
bagging_temperature = 0.2,od_type='Iter',verbose=False)
# 定義ngboost模型
ngb = NGBRegressor(Base=default_tree_learner, Dist=Normal, natural_gradient=True,verbose=False)
5.2 整合模型
在此,筆者還加了一種整合模型
# #整合多個個體學習器
# 這裡我僅保留了最好的四大基礎模型和一個最好的樹模型ngb,下圖也證實了模型的效果
stack_gen = StackingCVRegressor(regressors=(lr,ridge,lasso,enet,ngb),
meta_regressor=ngb,
use_features_in_secondary=True)
5.3 模型效果
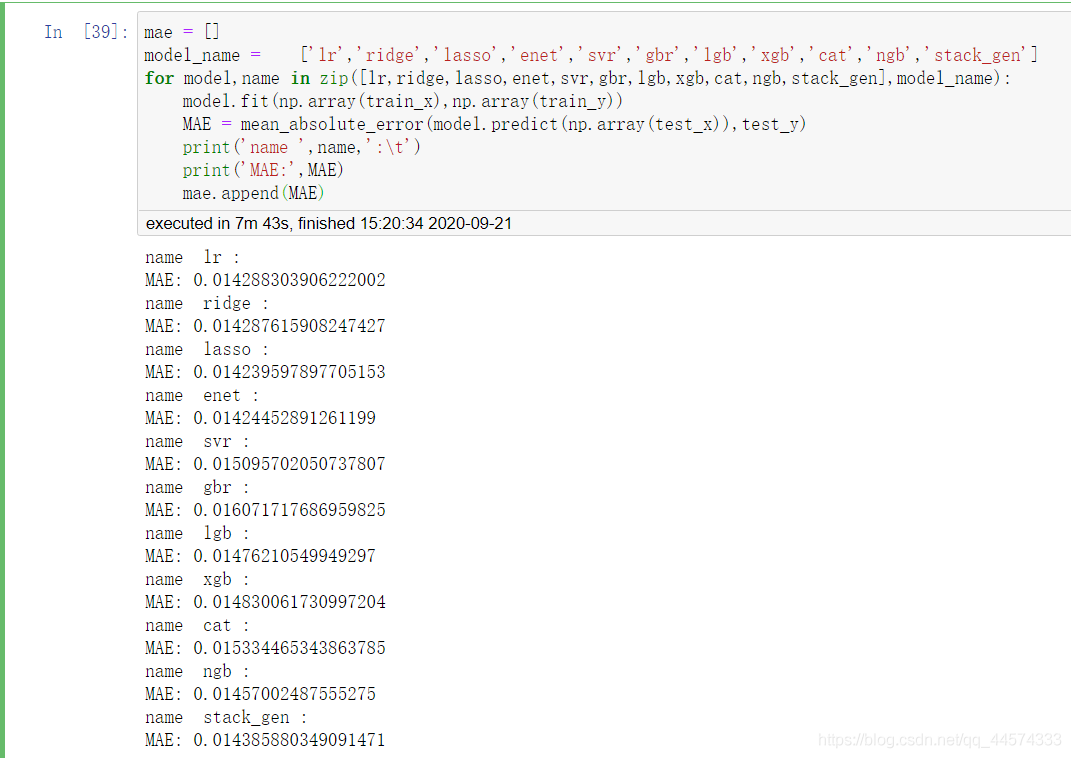
mae = []
model_name = ['lr','ridge','lasso','enet','svr','gbr','lgb','xgb','cat','ngb','stack_gen']
for model,name in zip([lr,ridge,lasso,enet,svr,gbr,lgb,xgb,cat,ngb,stack_gen],model_name):
model.fit(np.array(train_x),np.array(train_y))
MAE = mean_absolute_error(model.predict(np.array(test_x)),test_y)
print('name ',name,':\t')
print('MAE:',MAE)
mae.append(MAE)
sns.set()
plt.figure(figsize=(10,5))
plt.ylim(0.014,0.016)
plt.title('M A E')
plt.bar(model_name,mae)
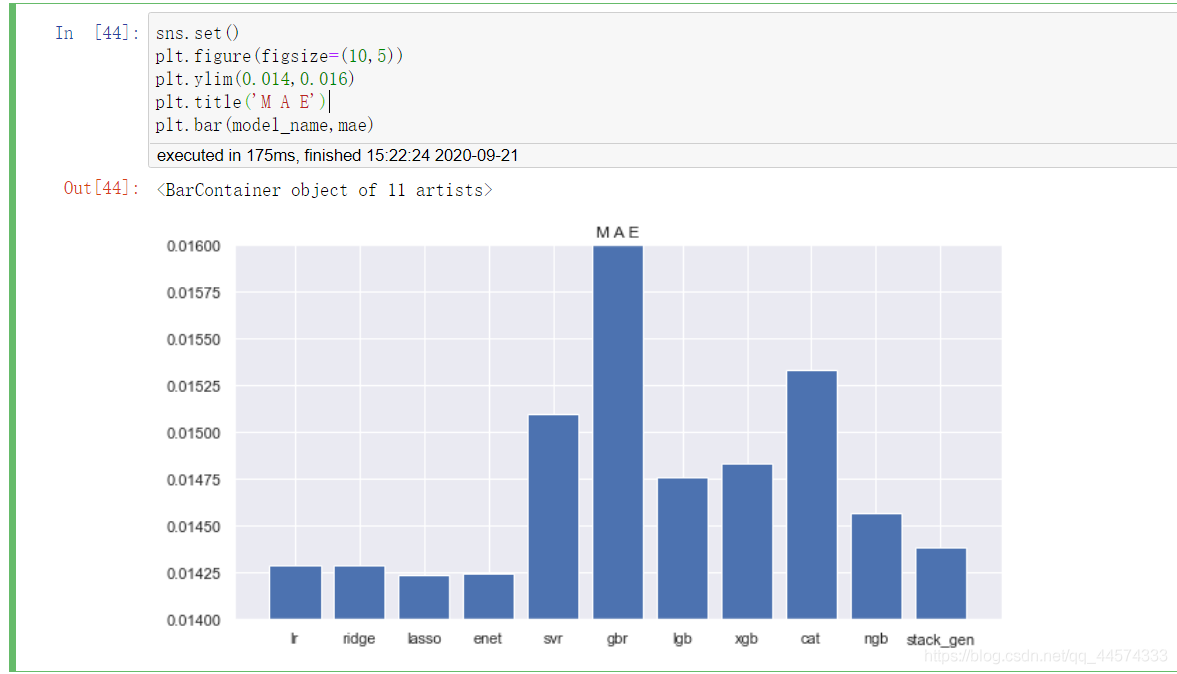
由上圖可知:
在對資料規範後,迴歸模型的效果如下:
lasso >= enet > ridge >= lr > stack_gen > ngb > lgb > xgb > svr > cat > gbr
5.4 模型融合
最後,筆者使用了一種加權組合的方法融合了所有模型
w = [1/i for i in mae]
w = [i/sum(w) for i in w]
# 綜合多個模型產生的預測值,作為多模型組合學習器的預測值
lr = lr.fit(train_x,train_y)
ridge = ridge.fit(train_x,train_y)
lasso = lasso.fit(train_x,train_y)
enet = enet.fit(train_x,train_y)
svr = svr.fit(train_x,train_y)
gbr = gbr.fit(train_x,train_y)
lgb = lgb.fit(train_x,train_y)
xgb = xgb.fit(train_x,train_y)
cat = cat.fit(train_x,train_y)
ngb = ngb.fit(train_x,train_y)
stack_gen = stack_gen.fit(train_x,train_y)
def blend_models_predict(test_x):
return (
lr.predict(test_x) * w[0]+
ridge.predict(test_x) * w[1]+
lasso.predict(test_x) * w[2]+
enet.predict(test_x) * w[3]+
svr.predict(test_x) * w[4]+
gbr.predict(test_x) * w[5]+
lgb.predict(test_x) * w[6]+
xgb.predict(test_x) * w[7]+
cat.predict(test_x) * w[8]+
ngb.predict(test_x) * w[9]+
stack_gen.predict(np.array(test_x)) * w[10]
)
blend_all_pre = blend_models_predict(test_x)
mae.append(mean_absolute_error(blend_all_pre,test_y))
model_name.append('blend')
sns.set()
plt.figure(figsize=(10,5))
plt.ylim(0.014,0.016)
plt.title('M A E')
plt.bar(model_name,mae)
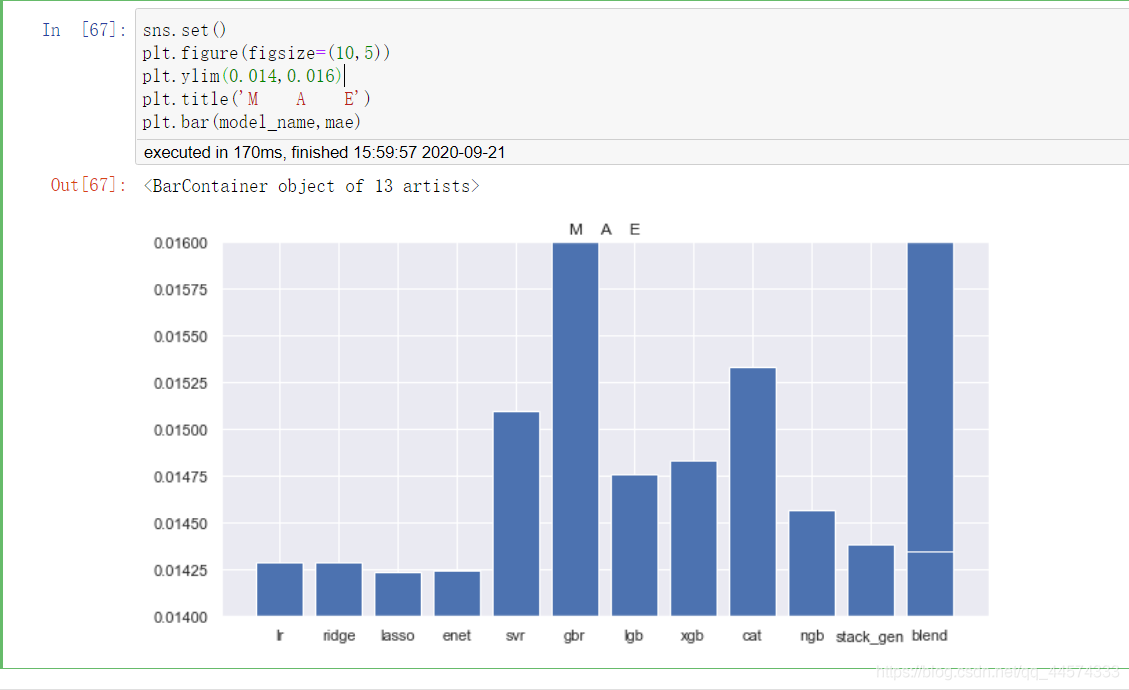
VI 總結
注:本實驗的結論僅是針對該資料集的結論。
本次實驗的實驗目的是測試各類迴歸模型對於該資料集的迴歸效果,找出最適合該資料集的迴歸模型進行實際應用。
(1)在無特徵工程+預設引數的情況下,我們得到了如下的模型效果:
● ridge >= lr > enet > lasso > ngb > lgb > cat > xgb
可以看出,「樸素簡單」的基礎模型是很值得肯定的,不僅訓練時間短,在這種情況下效果也是超過各類先進、複雜的樹模型。且在樹模型中NGBoost值得一用,但其訓練時間過長是一大缺憾。
(2)在資料規範化+優化調參的情況下,各類迴歸模型的效果如下:
● lasso >= enet > ridge >= lr > stack_gen > ngb > lgb > xgb > svr > cat > gbr
同樣,前四名還是由四大基礎模型lr、ridge、enet和lasso組成。值得一提的是,整合模型stack_gen排在了第五名,之後就是樹模型。但Catboost在該資料集的迴歸效果不佳。
愚見:筆者在得到上述結論時是有一定疑惑的,為什麼我們優秀的樹模型在迴歸上卻比不上基礎模型。且在筆者查詢Kaggle比賽上也發現了這一問題,很多回歸比賽基礎模型lr之類的本地cv確實會優於xgb,但其實和本實驗一樣,兩者差別並不大,但還是基礎模型本地cv更優,且最終topline所選擇的也是筆者上面使用的stack_gen的整合模型,而非單獨的基礎模型或樹模型。且在實際迴歸應用中,我們都知道xgb橫行金融預測。在此,筆者認為在資料的特徵工程不夠完美的時候,「一樹帶基礎模型」會更好、更穩定,之後再通過樹模型不斷優化將會更好。
完整ipynb程式碼檔案請見Github:
https://github.com/AmangAris/Summary