訊號課組(一) 訊號與系統 Review 1 訊號與系統綜述
文章目錄
1. 訊號的能量和功率
訊號主要分為兩種兩種,連續訊號和離散訊號,連續訊號取樣可以得到離散訊號,離散訊號也可以恢復成為連續訊號。
關於訊號本身最重要的概念是能量和功率。
對於電功率一般定義為:
1
t
2
−
t
1
∫
t
1
t
2
p
(
t
)
d
t
=
1
t
2
−
t
1
∫
t
1
t
2
1
R
v
2
d
t
\frac{1}{t_2-t_1}\int_{t_1}^{t_2}p(t)\,\mathrm dt= \frac{1}{t_2-t_1}\int_{t_1}^{t_2}\frac{1}{R}v^2\,\mathrm dt
t2−t11∫t1t2p(t)dt=t2−t11∫t1t2R1v2dt
這個例子給出了我們定義能量和功率的一個思路。由於訊號可能是複數,通過平方將為我們提供極大的便利。
隨後考慮去掉常數,更簡單地定義一個訊號的能量和功率。

2. 自變數變換
2.1. 時移和時變
高中考點:函數的平移和伸縮變換綜合應用
一般地討論:
- Q1:如何繪製 A x ( a t + b ) Ax(at+b) Ax(at+b):先向左平移 b b b,然後將橫座標變為原來的 1 a \frac{1}{a} a1,縱座標變為原來的 A A A倍。或者先壓縮,再平移 b a \frac{b}{a} ab
- Q2(DSP):通過 x [ n ] x[n] x[n],構成 x [ a n ] x[an] x[an]中可能出現無定義或者資訊損失。 a ∈ N , ∣ a ∣ > 1 a\in \N, |a| > 1 a∈N,∣a∣>1時,比如 a = 2 a = 2 a=2,此時奇數無定義,如果無定義處補齊稱為內插。若 ∣ a ∣ < 1 |a|<1 ∣a∣<1,比如 a = 1 2 a=\frac{1}{2} a=21時,資訊發生損失,稱為抽取。
2.2. 週期性
基波週期(Fundamental Period):最小正週期
思考
- Q1:無基波週期的周期函數?Dirichlet函數
- Q2:周期函數相加不一定是周期函數,比如 T 1 T 2 = π \displaystyle\frac{T_1}{T_2} = \pi T2T1=π,由於無最小公倍數,加和所得函數的週期將趨近無窮大。
- Q3: f f f和 g g g是 T T T為基波週期的函數,相加所得函數的可能週期為 T m , m ∈ N \frac{T}{m}, m\in\N mT,m∈N
- Q4:
f
f
f和
g
g
g分別是
T
T
T和
2
T
2T
2T為基波週期的函數,相加所得函數的可能週期為
2
T
2
m
+
1
,
m
∈
N
\frac{2T}{2m+1},m\in\N
2m+12T,m∈N
- 對兩個函數可以構造出更小的基波週期的函數,我們可以反向理解。我們可以通過先構造 2 T 3 \frac{2T}{3} 32T為基波週期的 H H H函數,然後同 f f f相加,就可以得到 g g g
- 分母不能為偶數,否則利用如上的方法,上下約分之後,得到 g g g的週期為 T T T,這是矛盾的。
2.3. 奇偶性
E v { x ( t ) } = △ x ( t ) + x ( − t ) 2 O d { x ( t ) } = △ x ( t ) − x ( − t ) 2 \mathrm{Ev}\{x(t)\}\xlongequal{\triangle}\frac{x(t)+x(-t)}{2}\\ \mathrm{Od}\{x(t)\}\xlongequal{\triangle}\frac{x(t)-x(-t)}{2} Ev{x(t)}△2x(t)+x(−t)Od{x(t)}△2x(t)−x(−t)
δ \delta δ函數為偶函數。
3. 典型訊號與重要的奇異訊號
3.1. 指數訊號和正弦訊號
復指數在工程上不存在,但為數學的分析提供了便利。
3.2. 單位階躍訊號
- 是衝激函數的積分。
- 用於擷取正向的訊號
3.3. 單位衝激訊號
極限定義比較直觀但數學上不易使用。利用Dirac定義和分佈函數定義更易使用。
∫
−
∞
∞
δ
(
t
)
d
t
=
1
δ
(
t
)
=
0
,
(
t
≠
0
)
\int_{-\infty}^{\infty}\delta(t)\,\mathrm dt = 1\\ \delta(t) = 0, (t \not =0)
∫−∞∞δ(t)dt=1δ(t)=0,(t=0)
4. 基本的系統性質
4.1. 因果性
不依賴未來情況,物理可實現的系統均具有因果性,表示如下:
y
(
t
)
=
∑
i
=
0
n
x
(
t
−
t
i
)
y(t) = \sum\limits_{i = 0}^n x(t-t_i)
y(t)=i=0∑nx(t−ti)
其中 t i ≥ 0 t_i \geq 0 ti≥0則稱為因果系統
例 y ( t ) = x ( t 3 ) y(t) = x(\frac{t}{3}) y(t)=x(3t)不是因果系統, t < 0 t<0 t<0時,系統取決於未來的情況。 y ( t ) = d x d t y(t)=\frac{\mathrm dx}{\mathrm dt} y(t)=dtdx當導數通過右導數定義時,就是非因果的。
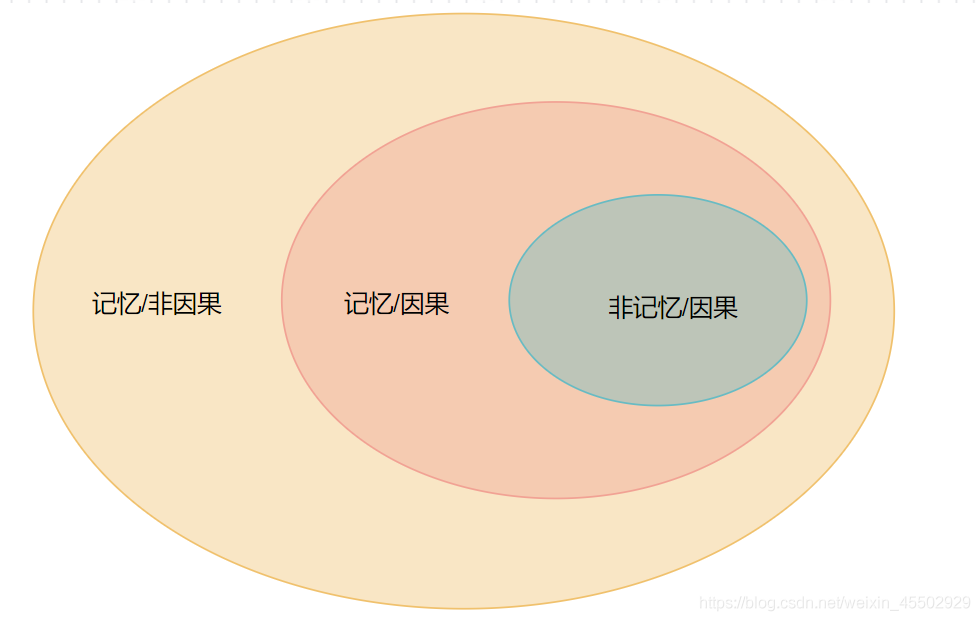
4.2. 記憶性
記憶性可以看成非因果系統的擴充。
這句話反過來說,非記憶系統一定是因果系統。
- 按照定義,非因果系統也稱為記憶系統
- 通常,利用導數定義的系統都會有記憶性(通過積分,可以把過去的情況呈現在當下)
- 實際系統中,記憶直接與能量儲存相關
4.3. 線性
齊次性+可加性
線性的證明通常判別兩個不同如數的輸出是否可以按權加和輸出。
反例:
y
(
t
)
=
x
(
t
)
+
1
y(t) = x(t) + 1
y(t)=x(t)+1
不是一個時不變系統。但是除去常數部分之後,具有線性,因而稱為增量線性系統
例:
y
(
t
)
=
2
y
(
1
)
+
x
(
t
)
y(t) = 2y(1) + x(t)
y(t)=2y(1)+x(t)
代入
t
=
1
t = 1
t=1,可求
y
(
1
)
=
−
x
(
1
)
y(1) = -x(1)
y(1)=−x(1),從而使得原式化簡為:
y
(
t
)
=
−
x
(
1
)
+
x
(
t
)
y(t)=-x(1)+x(t)
y(t)=−x(1)+x(t)
此例是一個線性系統。同上一例不同的是,看似是常數的
x
(
1
)
x(1)
x(1)實際上是與輸入函數相關的。
與輸入關聯和非關聯的輸出成分,分別對應後面講到的
4.4. 時不變性
輸入和輸出的時移特徵相同。
這一點說明如果內層有使其加倍的,那麼將成為時變的,因為時移也被再對映了。
比如:
y
(
t
)
=
x
(
2
t
)
y(t) = x(2t)
y(t)=x(2t)就是一個時變系統?
y
(
t
−
t
0
)
=
x
(
2
(
t
−
t
0
)
)
=
x
(
2
t
−
2
t
0
)
≠
x
(
2
t
−
t
0
)
y(t-t_0) = x(2(t-t_0)) = x(2t-2t_0) \not = x(2t - t_0)
y(t−t0)=x(2(t−t0))=x(2t−2t0)=x(2t−t0)
4.5. 穩定性
使系統傾向於收束。
穩定性判據:BIBO
也可以利用微分方程定性分析穩定。
4.6. 可逆性
可以建立輸入和輸出的一一對應
- 值域不重複(可求反函數)
- 不丟失定義域(原系統利用內插進行定義)
對應這兩個問題,有以下兩個例題:
- 反 例 1 \color{#FF0000}{反例}1 反例1 y ( t ) = x ( t ) + x ( 1 − t ) y(t) = x(t) + x(1-t) y(t)=x(t)+x(1−t)有 y ( 0 ) = y ( 1 ) = x ( 0 ) + x ( 1 ) y(0) = y(1) = x(0) + x(1) y(0)=y(1)=x(0)+x(1)
- 反 例 2 \color{#FF0000}{反例}2 反例2 y ( t ) = x ( 2 t ) y(t) = x(2t) y(t)=x(2t)是可逆的, y [ n ] = x [ 2 n ] y[n] = x[2n] y[n]=x[2n]是不可逆的。這個離散系統在對映過程當中發生了資料丟失。
另一個略顯複雜的例題:
y
(
t
)
=
x
(
t
)
(
a
+
cos
(
ω
t
)
)
y(t) = x(t)(a+\cos(\omega t))
y(t)=x(t)(a+cos(ωt))
首先,無論
x
x
x是什麼,只要
∣
a
∣
≤
1
|a| \leq 1
∣a∣≤1則一定會出現多個零點,反函數稱為多值函數。
分析
a
a
a足夠大時,才能使得波動的影響比較小,輸出與輸入近似為線性,使得其一 一對應。