1. HFE

Hierarchical Feature Engineering，簡寫 HFE，包含四個階段，分別是：

特徵工程階段（Feature engineering phase）
基於相關性的過濾階段（Correlation-based filtering phase）
基於資訊增益的過濾階段（Information Gain based filtering phase）
基於資訊增益的葉過濾階段（IG-based leaf filtering phase）

1.1. Feature engineering phase

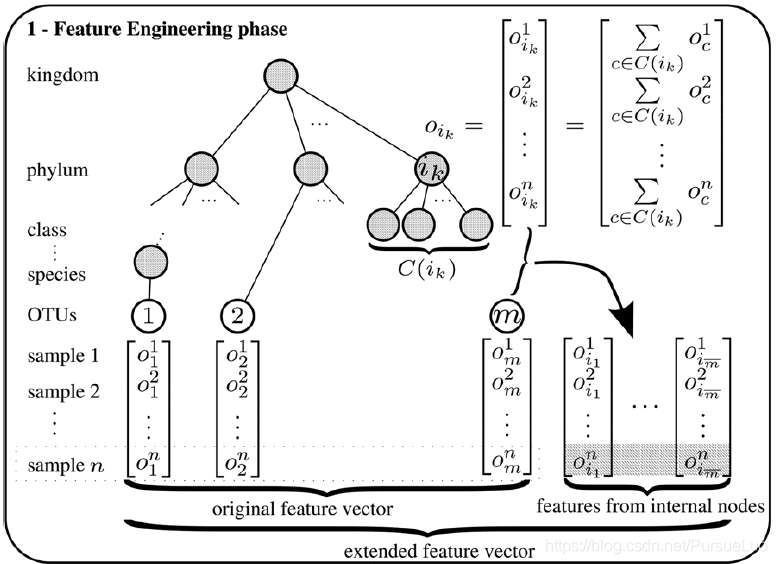
上圖中，樹結構共有 8 層。前七層是生物學的分類：界（Kingdom）、門（Phylum），綱（Class），目（Order）、科（Family）、屬（Genus）和種（Species）。論文中額外在最底層增加了一層：OTU 層。

資料集中原有的特徵向量表示為：

$(o^i_j)_{n \times m}= \begin{bmatrix} o^1_1 & o^1_2 & \dots & o^1_m \\ o^2_1 & o^2_2 & \dots & o^2_m \\ \dots & \dots & \dots & \dots \\ o^n_1 & o^n_2 & \dots & o^n_m \\ \end{bmatrix}, i \in [1, 2, \dots, n], j \in [1, 2, \dots, m].$

將較高分類單元 $i_k$ 視為潛在特徵，其相對丰度是自下而上的樹遍歷中各自孩子 $C$ 的相對丰度的累加和：

$o_{i_k} = \sum_{c \in C(i_k)} o_c.$

樹結構中的某個非葉子節點，是一個具有較高層次的潛在特徵，我們將其記為 $i_k$ ，它的孩子節點的集合記為 $C(i_k)$ ，則按照公式計算 $i_k$ 的相對丰度 $o_{i_k}$ ：

$o_{i_k} = \begin{bmatrix} o^1_{i_k} \\ o^2_{i_k} \\ \dots \\ o^n_{i_k} \\ \end{bmatrix} = \begin{bmatrix} \sum_{c \in C(i_k)} o^1_c \\ \sum_{c \in C(i_k)} o^2_c \\ \dots \\ \sum_{c \in C(i_k)} o^n_c \\ \end{bmatrix}.$

所有較高層次的潛在特徵，組成一個內部節點的特徵集合，表示如下：
$\begin{bmatrix} o^1_{i_1} & o^1_{i_2} & \dots & o^1_{i_{\overline{m}}} \\ o^2_{i_1} & o^2_{i_2} & \dots & o^2_{i_{\overline{m}}} \\ \dots & \dots & \dots & \dots \\ o^n_{i_1} & o^n_{i_2} & \dots & o^n_{i_{\overline{m}}} \\ \end{bmatrix}$

原始特徵和內部節點衍生出來的特徵，共同構成擴充套件特徵向量，其表示形式如下所示：
$\begin{bmatrix} o^1_1 & o^1_2 & \dots & o^1_m & o^1_{i_1} & o^1_{i_2} & \dots & o^1_{i_{\overline{m}}} \\ o^2_1 & o^2_2 & \dots & o^2_m & o^2_{i_1} & o^2_{i_2} & \dots & o^2_{i_{\overline{m}}} \\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ o^n_1 & o^n_2 & \dots & o^n_m & o^n_{i_1} & o^n_{i_2} & \dots & o^n_{i_{\overline{m}}} \\ \end{bmatrix}$

1.2. Correlation-based filtering phase

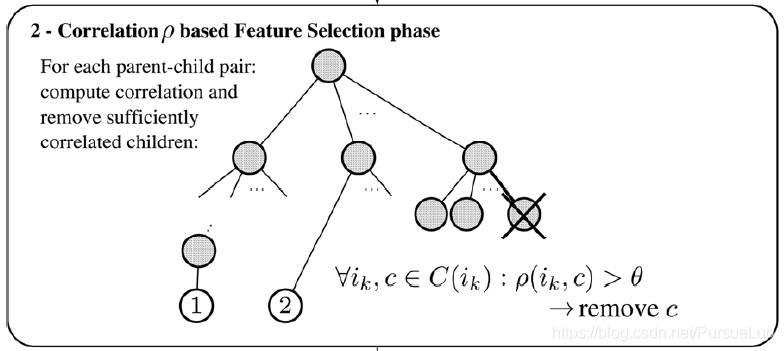
在這裡插入圖片描述
對於層級中每對「父親-孩子」，皮爾遜相關係數（Pearson correlation coefficient） $\rho$ 是父親節點和孩子節點的一組向量計算出來的。
如果 $\rho$ 比預定義的閾值 $\theta_{p}$ 大，那麼移除孩子節點；否則保留孩子節點作為層級結構的一部分。

$\text{operation} = \begin{cases} \text{remove}, \text{ if } \rho > \theta_{p}; \\ \text{retain}, \text{ otherwise.} \end{cases}$

對於任意的非葉子節點 $i_k$ ，它的孩子節點集合是 $C(i_k)$ ，則

$\forall i_k, c \in C(i_k)$ ,
$\text{operation } = \begin{cases} \text{remove } c, \text{ if } \rho(i_k, c) > \theta_{p}; \\ \text{retain } c, \text{ otherwise.} \end{cases}$

1.3. Information Gain ( $I G$ ) based filtering phase

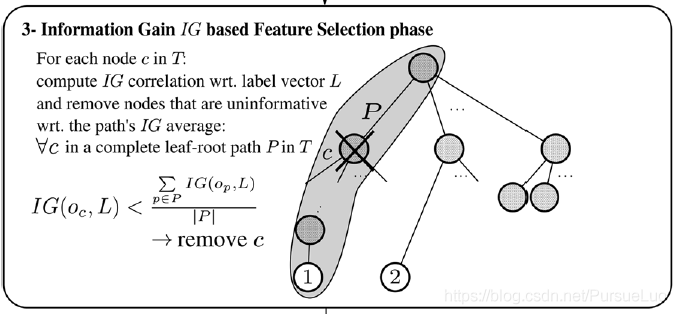
在這裡插入圖片描述

根據上一階段保留的節點，從葉子到根（即每個 OTU 的世系）構建所有路徑。

對每條路徑而言，計算路徑上每個節點關於標籤/類別 $L$ 的 $I G$ 。

平均 $I G$ 作為閾值 $\theta$ ，用於丟棄具有較小 $I G$ 值或者零值的節點。

需要注意的是，具有不完整路徑上的葉子節點不參與這一步，這些葉子節點將在 1.4. 中處理。

公式表示如下：
$\theta_{ig} = \frac{\sum_{p \in P} IG(o_p, L)}{\left| P \right|}$

$\forall c \text{ in a complete leaf-root path } P \text{ in } T$ ,

$\text{operation } = \begin{cases} \text{ remove } c, \text{ if } IG(o_c, L) < \theta_{ig}; \\ \text{ retain } c, \text{ otherwise.} \end{cases}$

1.4. $I G$ -based leaf filtering phase

為了處理 OTUs 中完整的分類資訊，
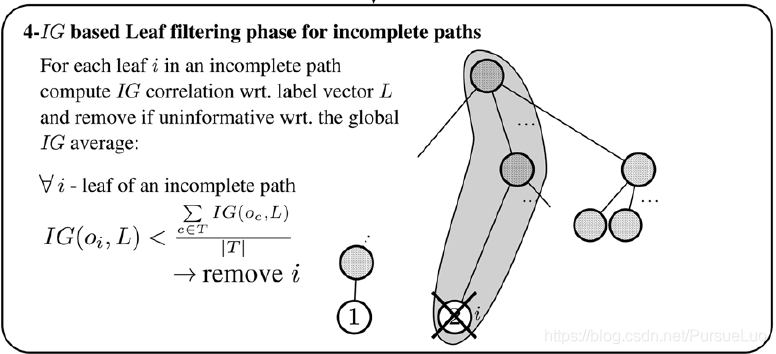
在這裡插入圖片描述
對於那些具有不完整分類資訊的 OTU（路徑不完整： incomplete paths），如果它的 $I G$ 大於 1.3. 中完整路徑中所有節點的全域性平均 $I G$ 值，那麼保留該節點；否則，丟棄該節點。

用公式表示：

$\theta_{t} = \frac{\sum_{c \in T} IG(o_c, L)}{\left| T \right|}.$

$\text{operation } = \begin{cases} \text{ remove } c, \text{ if } IG(o_i, L) < \theta_{t}; \\ \text{ retain } c, \text{ otherwise.} \end{cases}$

2. DOI

https://doi.org/10.1186/s12859-018-2205-3

論文閱讀報告：Taxonomy-aware feature engineering for microbiome classification，Mai Oudah and Andreas Hen

文章目錄