解析DFS
DFS介紹:
DFS 全稱是 Depth First Search ,中文名是深度優先搜尋,是一種用於遍歷或搜尋樹或圖的演演算法。
該演演算法講解時常常與 BFS 並列,但兩者除了都能遍歷圖的連通塊以外,用途完全不同,很少有能混用兩種演演算法的情況。
DFS 最顯著的特徵在於其遞迴呼叫自身 。同時與 BFS 類似,DFS 會對其存取過的點打上存取標記,在遍歷圖時跳過已打過標記的點,以確保 每個點僅存取一次 。符合以上兩條規則的函數,便是廣義上的 DFS。
DFS的思路:所謂深度優先,就是說每次都嘗試向更深的節點走。
DFS優化:DFS是暴搜,改寫成記憶化搜尋之類的,或者剪枝(break一些分支)都可以優化(待補充)。
DFS的板子大致如下:
void dfs(int step)
{
if(走到邊界)
{
操作();//輸出答案等
return;
}
else
{
for()//列舉方向等
if(滿足進一步搜尋條件)
{
標記為存取;
search(step+1);
收回標記;//回溯
}
}
}
這個板子看上去比較易懂,但其細節還是值得思考的,下面以幾個經典題目為例子,解析DFS相關語句。
例題1:求1-n全排列
題目大意:就是求1-n全排列
首先,我們可以模擬一下求全排列這個過程(參考了《啊哈!演演算法》)
這裡模擬n=3的情況
我們有三張卡牌1,2,3 並且有三個卡槽,現在要將三張牌放入三個卡槽中,從第一個卡槽開始出發,首先我們向第一個卡槽放入1,然後繼續向前走,依次放入2,3,並向前走(到第三個卡槽後一步),此時,得到了第一個序列1,2,3。(靈魂配圖預警)
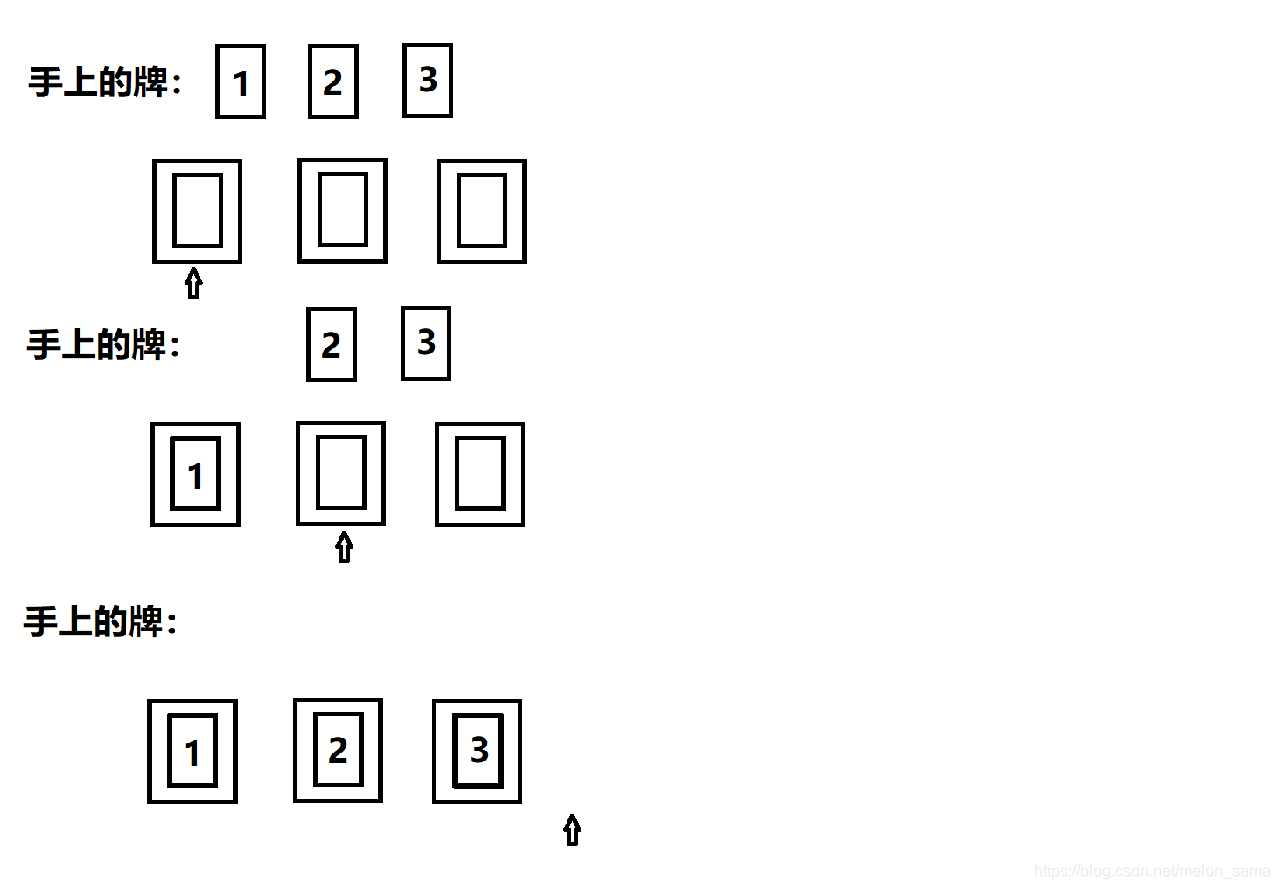
而且,我們的手中已經沒有卡牌了,所以要回退,在回到第三個卡槽的時候,收回第三張牌(這裡是3),然而此時若放下3便和剛才的情況重複,於是繼續回退收回第二張牌(這裡是2)。在完成收回第二張牌的動作之後,我們手上有了2,3。於是便可以將3放入第二個卡槽,向前走,將2放入地三個卡槽,得到第二個序列1,3,2。
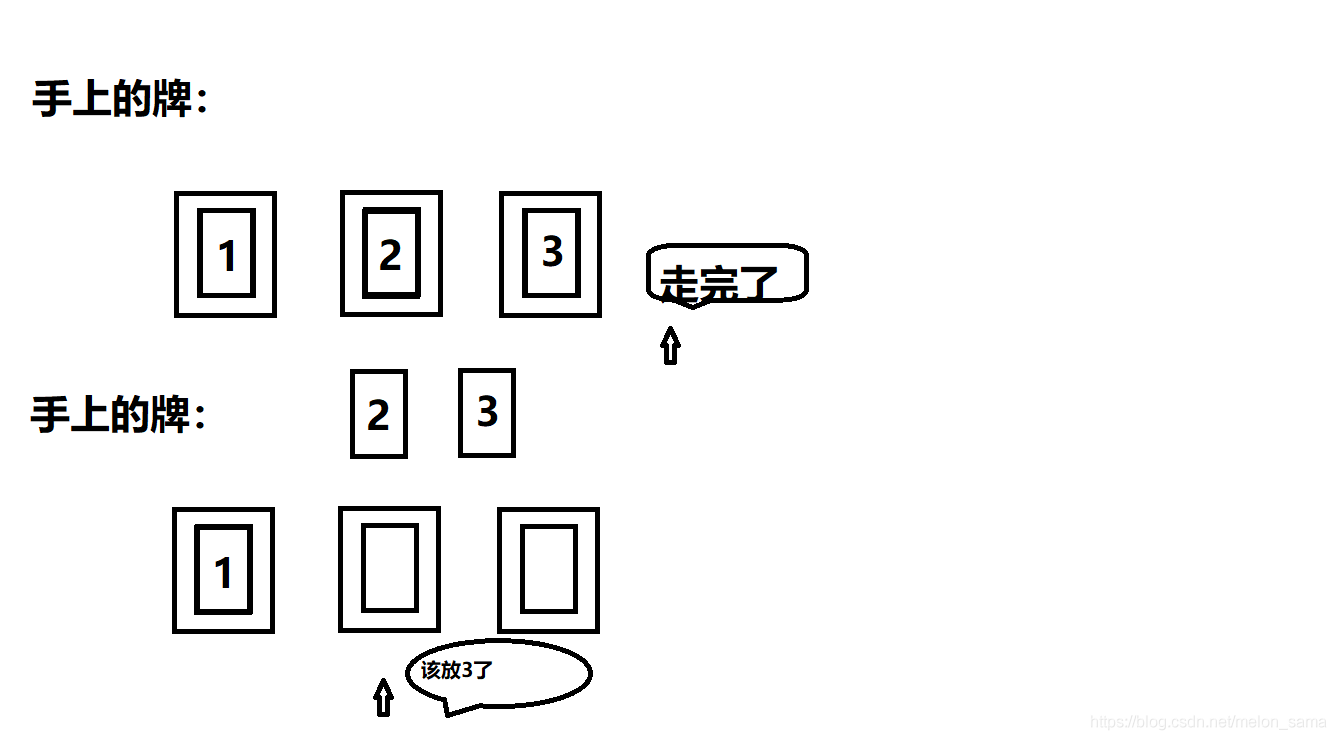
類似地,可以得到1-3的全排列。
模擬完後我們就可以輕鬆寫出程式碼了
現在上程式碼:(先看看註釋理解一下吧)
#include<iostream>
using namespace std;
int a[100001],n;
bool book[100001];//判斷是否被存取
void dfs(int step){
// if(滿足所需要的條件) { 相應的操作;return;}
if(step==n+1){
for(int i=1;i<=n;i++) printf("%d ",a[i]);//列印
cout<<endl;
return;
}
//列舉
for(int i=1;i<=n;i++)
{
if(book[i]==0)
{
a[step]=i;//記錄資料
book[i]=1;//記錄相應的數已經被存取
dfs(step+1);//進一步搜尋
book[i]=0;//恢復到未被存取
}
}
}
int main(){
cin>>n;
dfs(1);//從一開始搜尋並且列印
return 0;
}
很多語句都是很好理解的,但是不是還是一頭霧水
那麼只要解決幾個難懂的問題就可以了
現在需要解析的是:
Q1:這個函數實現了什麼?
先撇開判定搜完一輪的if語句,這個函數其實就是for迴圈套著for迴圈,他的本質其實與n個for迴圈無異,但是為什麼要這樣子寫?就是因為n可能很大,用for一直寫可能實現不了。所以這個函數的功能就是暴力依次列舉1-n的全排列(可以試試n=3只用for迴圈實現就可以理解了)。
Q2:如下,這裡的return語句到底返回到了哪裡?
// if(滿足所需要的條件) { 相應的操作;return;}
if(step==n+1){
for(int i=1;i<=n;i++) printf("%d ",a[i]);//列印
cout<<endl;
return;
}這個問題困擾了我很久,在被dalao教做人與dalao討論後,我得到了較為清楚的解釋。
return的作用無非是返回,結束該層的函數,而在這個函數中,便是結束了一個dfs(n+1),回到了dfs(n)中(第n層迴圈),並繼續執行dfs(n)中的語句,比如這裡是回到第二個語句中:
1 dfs(step+1);
2 book[i]=0;//恢復到未被存取 拿剛才的模擬過程來說:就是我們已經走到第三個卡槽之後,開始回退。
Q3:為什麼回退之後拿回第一張牌(比如模擬中的第三個卡槽的牌)之後,不會出現立即將該牌放入相應卡槽出現死迴圈的現象呢?
以模擬過程為例,回到程式中,不難發現,此時的迴圈中的i=4,已經跳出這層迴圈了,自然地,回到了上一層迴圈(也就是第二個卡槽中,實現了回退)。
(待補充)
解決了這些問題之後,大概就能夠比較清楚地瞭解DFS的工作原理了。
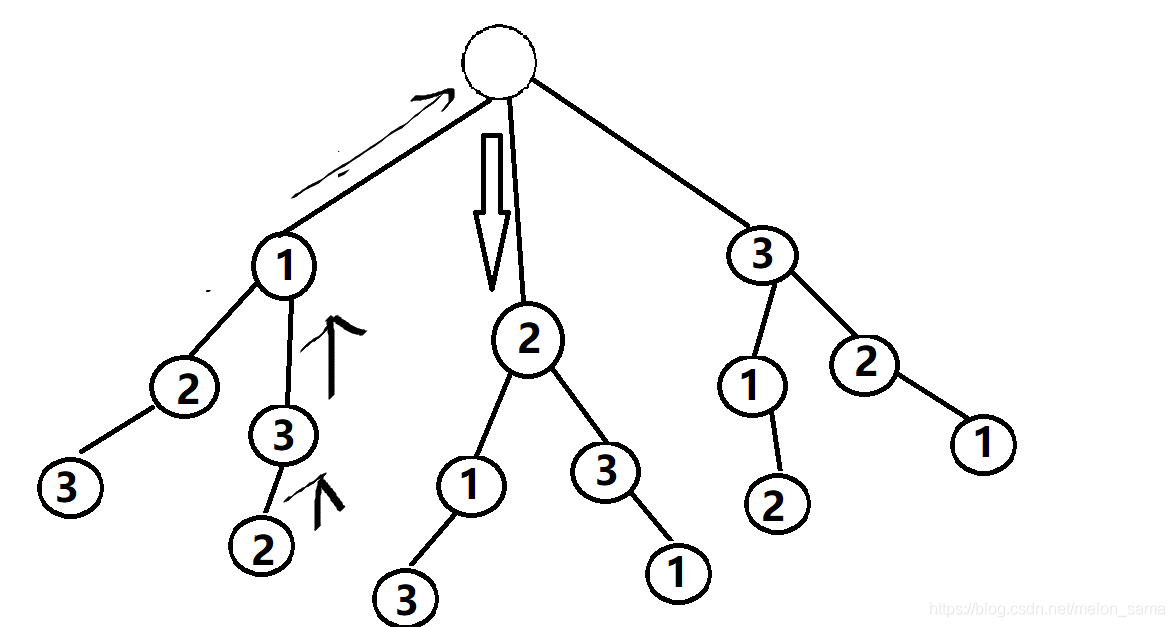
下面用遞迴樹來刻畫DFS實現的過程以加深理解(以求1-3的全排列為例):
前方靈魂圖示預警
從第一個結點出發,開始搜尋~
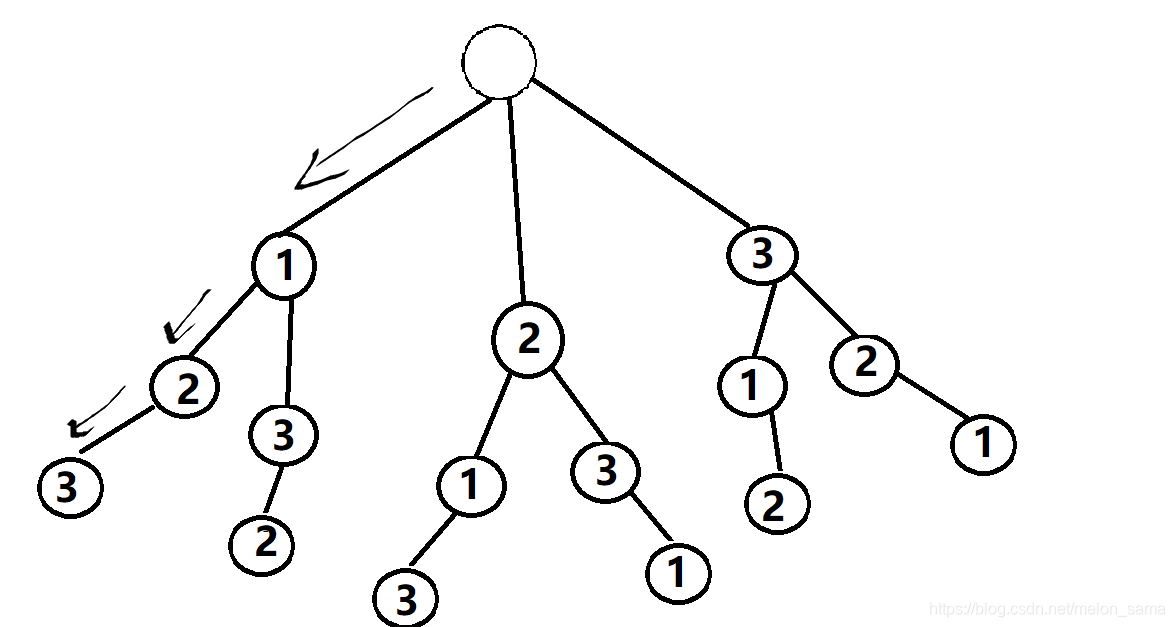
根據DFS的思路,搜到無路可走開始回退。
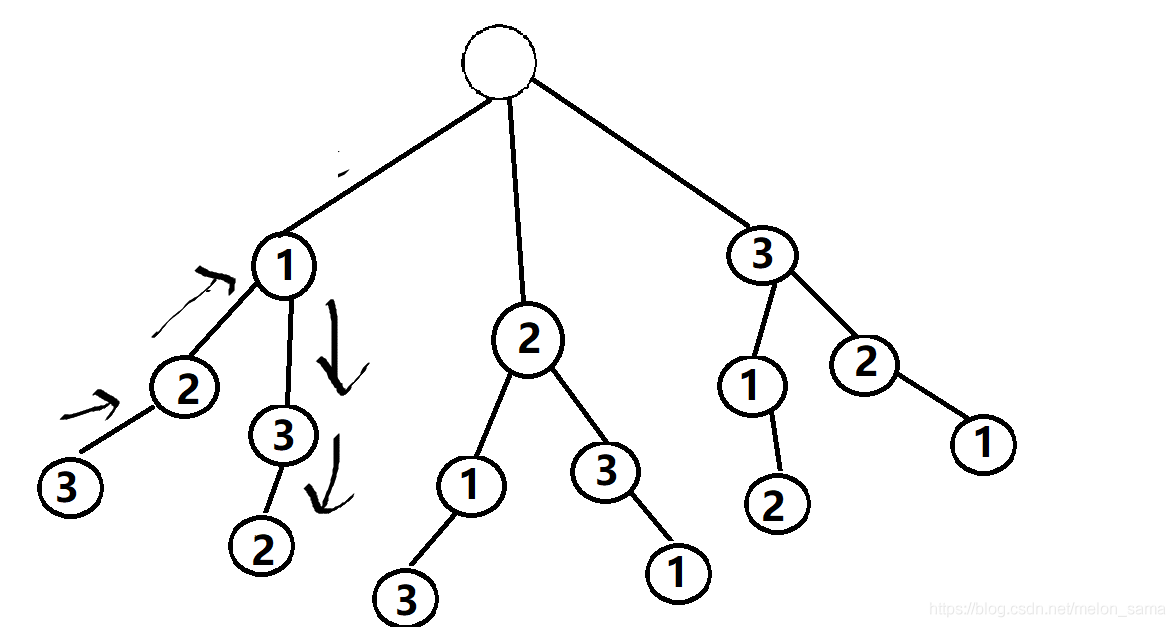
類似地,繼續往下搜,直到得到所有答案:
例2:迷宮
題目大意:就是給你一個迷宮(廢話),迷宮有一些障礙,需要你求從起點座標到終點座標的方案總數。
下面貼出程式碼以供參考:
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
typedef unsigned long long ll;
int map[10][10];//存圖
int x,y;//記錄起點座標
int px,py;//記錄終點座標
int m,n,t;
int a,b;//記錄障礙點
ll ans=0;//初始化ans
const int dx[4]={0,0,-1,1};//x direction
const int dy[4]={1,-1,0,0};//y direction
void dfs(int x,int y){
if(x==px&&y==py)//到達終點
{
ans++;
return;
}
else{
for(int i=0;i<4;i++)
{
int kx=x+dx[i];int ky=y+dy[i];//進行移動
//判定是否越界 有障礙 已經存取過
if(kx<1||ky<1||kx>m||ky>n||map[kx][ky]==1||map[kx][ky]==2)continue;
map[kx][ky]=1;//標記已經存取
dfs(kx,ky);
map[kx][ky]=0;
}
}
}
int main(){
cin>>n>>m>>t;
cin>>x>>y;cin>>px>>py;
while(t--){
cin>>a>>b;
map[a][b]=2;
}
map[x][y]=1;//初始化,標記起點為已經存取
dfs(x,y);//從起點開始搜
cout<<ans;
return 0;
}