BCH通道編譯碼
通訊的目的是要把對方不知道的訊息即時可靠地(有時還要祕密地)傳送給對方。當通道中存在干擾,可能使傳送的訊息出錯。數位通訊中,通常使用糾錯碼技術來進行差錯控制,這樣可以提高資料傳輸的可靠性。
BCH碼就是一種應用廣泛的能糾正多重錯誤的分組碼,具有極佳的糾錯效能。本文對BCH碼的原理進行深入分析,介紹BCH的編解碼原理。重點介紹了BCH編碼解碼的計算方法以及BCH編碼的效能分析。最後,本文采用MATLAB編寫相應的BCH編解碼程式碼進行模擬和誤位元速率分析,並在Simulink中搭建BCH模組進行誤位元速率統計分析。本文所作的研究成果具有一定的科研價值,為BCH的進一步研究或在硬體系統上的實現提供了良好的理論基礎。
1.1 本課題研究背景
數位訊號在傳輸系統中傳輸時,不可避免受到各種因素的干擾,使到達接收端的數位訊號中混有噪聲,從而引發錯誤判決,為了抗擊干擾,必然要利用糾錯碼的差錯控制技術。
糾錯碼的分類有以下幾種:
·按照對資訊序列處理方式的不同,分為分組碼與折積碼兩大類,在分組碼中按照碼的結構特點,又可分為迴圈碼和非迴圈碼。
·根據資訊位與校驗位之間的關係分為線性碼與非線性碼。
·按照適用的差錯型別,分成糾隨機差錯碼和糾突發差錯碼兩種,也有介於中間的糾隨機/突發差錯碼。
·按構碼理論,有代數、幾何、算術、組合碼等。
除了上述分類外,有多少觀察問題的角度,就有多少分類方法。比如,按每個碼元的取值,可以分為二進位制碼與多進位制碼;按碼字之間的關係,有迴圈碼和非迴圈碼之分;不同的分類方法只是從不同的角度抓住碼的某一特性加以歸類而己,並不能說明某個碼的為全部特性。比如某線性碼可能同時又是分組碼,迴圈碼,糾突發差錯碼,代數碼,二進碼。
1.2 線性分組碼和迴圈碼
線性分組碼是分組碼中最重要的一類碼,用(n,k)表示,其中n表示碼長,k表示資訊位數目,n-k=r表示校驗位數目,二進位制(n,k)線性分組碼可以定義為GF(2)域上的n維線性空間Vn中的一個k維子空間。
線上性分組碼中有三個重要引數,分別為位元速率、碼的漢明距離和漢明重量。位元速率R=k/n,它說明了分組碼傳輸資訊的有效性。碼的漢明距離指兩個碼字對應位上碼元不同的個數,簡稱距離。漢明重量指碼字中非零碼元的個數,簡稱重量。在(n,k)線性分組碼中,將任兩個碼字距離的最小值稱為最小距離d0。由於線性分組碼是群碼,由群碼的封閉性可知,若碼字C1,C2均是(n,k)碼的碼字,則C1+C2也必是該分組碼的另一碼字,可見(n,k)線性分組碼的最小距離等於非零碼字的最小重量。最小距離d。直接在理論上決定了該碼的檢錯和糾錯能力。
迴圈碼是線性分組碼中最重要的一個子類,它的代數結構比較清晰,編譯碼相對於其它碼來講簡單且易於實現,因此迴圈碼在差錯控制系統中得到廣泛的應用,BCH碼就是迴圈碼中很重要的一類碼。
在GF(2)上的n維線性空間氣中,若是的一個k維子空間,對任何,有,則是迴圈碼。
由編碼理論推匯出的迴圈碼糾錯能力只是一個理論值,在現實中能否達到這個理論值還與所用的譯碼方法有關。一個好的譯碼方法,不僅應使糾錯能力能夠達到理論極限,而且應能高速度、低成本地實現,因為速度和成本有時會成為某種碼能否實用的決定性因素。
譯碼電路通常要比編碼電路複雜得多,因此我們說,理論的複雜性常體現在編碼上,而工程的複雜性常體現在譯碼上。從對輸入訊號的量化程度,譯碼可分為硬判決譯碼(BSC通道)和軟判決譯碼(DMC通道)。
軟判決由於採用了大於2的量化級數,能更充分地利用接收訊號包含的資訊,與硬判決相比,在AWGN通道、10-2-10幣誤位元速率範圍時可有2dB的編碼增益,因此代表了譯碼的發展方向。從差錯控制方式,譯碼可分為糾錯和檢錯兩種。糾錯譯碼器總有輸出,但有兩種可能:一是收碼的差錯數量在糾錯能力之內,譯碼器認定的正確真的是正確。二是差錯數量超出糾錯能力,譯碼器認定的正確其實是錯的。由於難以判斷差錯數量是否超出糾錯能力,糾錯譯碼器不能保證輸出資料完全可靠,所以糾錯譯碼器常用於數位語音、影象、視訊訊號的向前錯誤更正(FEC)中。
1.3 BCH編碼的研究和應用
BCH碼於1959年由霍昆格姆、1960年由博和雷-查德胡裡三人分別提出,並以這三個發現者的名字命名。BCH碼是迄今為止所發現的一類很好的線性糾錯碼類。它的糾錯能力很強,特別在中等和短碼長條件下,BCH碼的效能接近理論上的最佳值,並且構造方便,編碼簡單。特別是它具有嚴密的代數結構,在代數編碼理論中起著重要作用。BCH碼是迄今為止研究得最為詳盡、瞭解得最為透徹、取得成果最多的一類線性分組碼。
1960年彼得遜從理論上解決了二進位制BCH碼的譯碼演演算法,奠定了BCH碼譯碼的理論基礎。稍後,格林斯坦和齊勒爾把它推廣到多進位制。1966年伯利坎普利用迭代演演算法譯BCH碼,從而大大加快了譯碼速度,從實際上解決了BCH碼的譯碼問題。由於BCH碼效能優良,結構簡單,編譯碼裝置也不太複雜,使得它在實際使用中受到工程技術人員的歡迎,是目前用得最廣泛的碼類之一。
在英國模擬行動通訊系統中,基站採用了具有糾正2位隨機錯誤能力的BCH(40,28)碼,移動臺採用了可糾正2位隨機錯誤的BCH(48,36)碼;在我國無線尋呼系統中,採用了BCH(31,21)碼加一位奇偶校驗位作為FEC方式;在視訊編碼協定H.261、H.263中採用了BCH(511,493)碼進行視訊糾錯。
第三章 BCH碼理論簡介
3.1 BCH碼簡介
BCH碼是迴圈碼的一個重要子類,它具有糾多個錯誤的能力,BCH碼有嚴密的代數理論,是目前研究最透徹的一類碼。它的生成多項式與最小碼距之間有密切的關係,人們可以根據所要求的糾錯能力t很容易構造出BCH碼,它們的譯碼器也容易實現,是線性分組碼中應用最普遍的一類碼。
3.1.1伽羅華域
編碼原理中最基本、最重要的域是二元伽羅華域GF(2)及二元擴域GF(2m)。有限正數集合F={0,1,2,3,…,q-1}(q是素數)在模q加、模q乘運算下構成一個q階有限域,又稱伽羅華(Galois)域,記為GF(q)。當q=2時,就是二元域GF(2)。
在有限域中定義的運算滿足閉合性,即有限域GF(q)上任意兩個元素A、B對運算⊙滿足:A⊙B∈GF(q)。
如果p是素數,m是正整數,GF(2m)的最小子域是GF(p),p稱為GF(2m)的特徵,在特徵為2的伽羅華域中,任一域元素B有-B=B。
設B為GF(q)上的任一元素,則B=Bq。
每個伽羅華域GF(q)至少包含有一個本原元素α,且GF(q)上除零以外的其它任意域元素均可表示為本原元素的乘冪。
任一有限域均可由一本原多項式來構成,有限域的任一多項式對本原多項式求模,可得到一個次數低於本原多項式次數的多項式,即有限域的元素。
·加法運算
域元素的加法運算,即根據域元素表格,轉換成對應的m-1次多項式係數(m重向量)。兩個域元素相加等效於兩個m-1次多項式的同次項係數模2相加,即互斥或運算。
·乘法運算
乘法有三種實現途徑:
第一就是把域元素對應的多項式係數直接移位,比如a×b,只要找到b對應的冪次,假設是x,將a左移x次,每次左移之前判斷移位前的值高位是否為1,如果是1,移位後與本原多項式除高次冪後的多項式相加;
第二種方法就是從b的高位開始,如果b7=1,將a左移7次,如果b6=1,將前面左移結果再左移6次。
第三種方法是直接把域元素的指數相加求模2m-1。這裡採用第三種方法。
·求模運算
因為2^m-1轉換成二進位制數永遠是全1,所以根據這個特點,可以用下面的方法求模。把二進位制形式的數從低位起每m位元分割,高位不滿m位元用0補齊。然後高位元欄每出現一個1,就把高位減去1,然後把低位加1,這樣迴圈操作直到高位元欄變成全0。




3.3 BCH譯碼理論介紹
BCH碼的譯碼可以分為時域譯碼和頻域譯碼兩種。
頻域譯碼是把碼字看作一個時域數位序列,對其進行有限域的離散傅氏變換(DFT)將它變換到頻域,然後利用其頻域特點譯碼。這樣通過對頻域伴隨式的運算解出指示差錯位置的關鍵方程,再通過離散傅氏反變化還原成時域的糾錯訊號。
時域譯碼是把碼字看作時間軸上的訊號序列,利用碼的代數結構進行譯碼。由於取有限域離散傅氏變換增加了複雜度,頻域譯碼的實現一般較時域譯碼複雜,因此採用快速傅氏變換(FFT)的頻域譯碼只在某些特殊情況下對特定碼長(比如n等於2的冪次)的譯碼優於時域譯碼,而在一般情況下應用最廣泛的是時域譯碼。其中BCH譯碼器的基本結構如下所示:
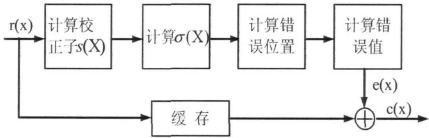
圖3-1 BCH譯碼器基本結構框圖
通常,我們在MATLAB中設計演演算法分三個步驟:
·STEP1:由接收到的R(x)計算出伴隨式S;
·STEP2:由伴隨式得出錯誤圖樣E(x);
·STEP3:由R(x)-E(x)得到估值碼字c(x)。
5.2 BCH編碼的系統模擬
我們根據前面的理論分析,編寫MATLAB程式碼。這裡,我們根據要求,進行(511,493)(4095,4035)兩種引數的BCH編碼,其MATLAB編碼函數如下所示:
function code=bchencoder(data,genpoly,n,k);
bb=zeros(1,n-k);
for i=k:-1:1
feedback = xor(data(i), bb(n-k));
if feedback~=0
for j=n-k:-1:2
if genpoly(n-k-j+2)~=0
bb(j)=xor(bb(j-1),feedback);
else
bb(j)=bb(j-1);
end
end
bb(1)=feedback;
else
for j=n-k:-1:2
bb(j)=bb(j-1);
end
bb(1)=feedback;
end
end
code=[bb,data];
我們在頂層對其進行呼叫,呼叫過程如下程式碼:
for j=1:nwords
encoded_data((j-1)*n+1:(j-1)*n+n)=bchencoder(message((j-1)*k+1:(j-1)*k+k),genpoly,n,k);
end
輸入資訊為:
………… 1 1 0 1 1 0 0 1 1 1 …………………………
通過BCH編碼之後,得到BCH編碼資訊:
………… 1 1 0 0 0 1 0 0 1 0 …………………………
5.3 BCH譯碼的系統模擬
本系統譯碼我們將採用應用十分普遍的‘錢搜尋’法進行譯碼,前面我們已經簡單的介紹了該演演算法, 其MATLAB程式碼實現過程如下所示:
lambda_v = zero;
accu_tb=gf(ones(1, t+1), m);
for i=1:n,
lambda_v=lambda*accu_tb';
accu_tb = accu_tb.*inverse_tb;
if(lambda_v==zero)
error(1,n-i+1)=1;
else
error(1,n-i+1)=0;
end
end
found = find(error(1,:)~=0);
for i=1:length(found)
location=found(i);
if location <= k;
rec_data(n-location+1)=rec_data(n-location+1)+one;
end
end
decoded_data((j-1)*k+1:(j-1)*k+k)=rec_data(n-k+1:n);
我們將編碼之後得到的訊號輸入BCH譯碼部分,輸出結果:
………… 1 1 0 1 1 0 0 1 1 1 …………………………
5.2.4 不同引數的BCH編解碼效能分析
本章我們將重點對幾種不同引數的BCH碼進行了模擬。系統訊雜比的分析我們主要採用:‘semilogy’進行模擬。我們分別對(511,493)(4095,4035)進行模擬,然後不改變n,k兩個引數,改變其糾錯能力進行模擬,從而判斷BCH編解碼的效能。

圖5-1 n=511,k=493,t=11條件下訊雜比
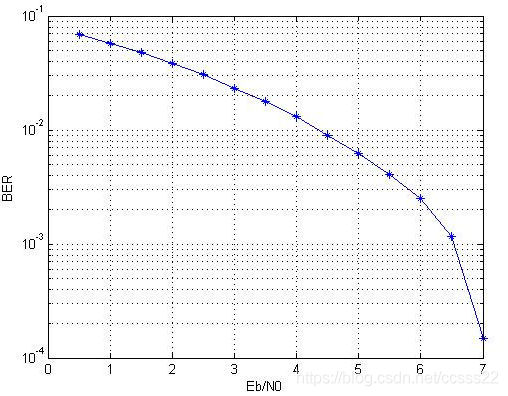
圖5-2 n=4095,k=4035,t=11條件下訊雜比
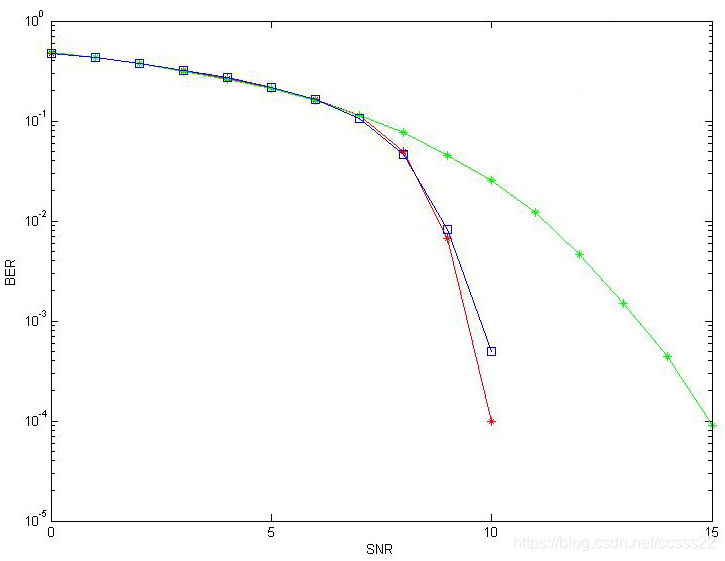
圖5-3 BCH編碼和不編碼的效能對比(綠色為未通過編碼)
從模擬結果可以看出,對於糾錯能力相同的BCH碼,碼字長度短的相對碼字長度長的效能好,且平均模擬一個碼字所耗費的時間少。分析原因,是因為在相同的通道條件下,每個碼元出現錯誤的概率是相同的,對於碼字長度長的BCH碼,平均每個碼字中出現錯誤的碼元個數多,所以對於糾錯能力相同的BCH碼,碼字長度長的效能差。
以上我們詳細介紹了MATLAB的BCH編解碼和訊雜比分析,下面我們將在Siumlink中進行BCH實際模擬,在本系統,我們將基於BPSK進行模擬分析。
不加BCH的BPSK系統如下所示:

圖5-4 BPSK模擬系統
其模擬結果如下所示:

加入BCH編解碼,其系統如下所示:
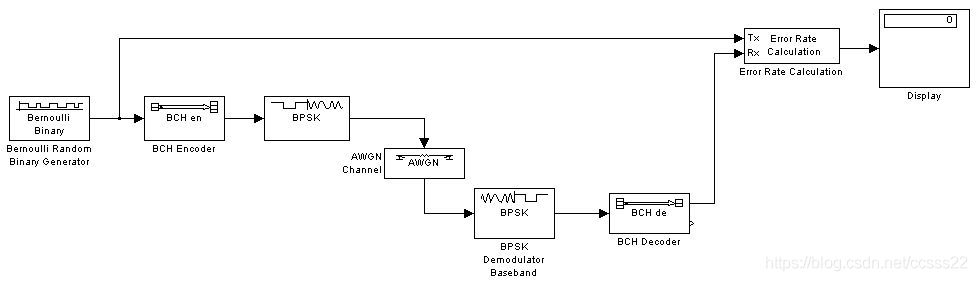
圖5-5 BCH模擬系統
其模擬結果如下所示:

由上圖可見,加上BCH編解碼後,新能得到大大改善。
·編碼和譯碼
clc;
clear;
close all;
m=9;%輸入引數6
k=493;%輸入引數4
snr=1;
n=2^m-1;
period=1000;
nwords = ceil(1000/k);
[genpoly,t] = bchgenpoly(n,k);
simplified = 1;
alpha = gf(2, m);
zero = gf(0, m);
one = gf(1, m);
message=randint(1,nwords*k);
message1=gf(message);
decoded_data=gf(zeros(1,nwords*k));
alpha_tb=gf(zeros(1, 2*t), m);
for i=1:2*t,
alpha_tb(i)=alpha^(2*t-i+1);
end;
%BCH編碼
for j=1:nwords
encoded_data((j-1)*n+1:(j-1)*n+n)=bchencoder(message((j-1)*k+1:(j-1)*k+k),genpoly,n,k);%由高位到低位
end
%新增噪聲
sigma=sqrt(1/(10^(snr/10))/2);
datalength=length(encoded_data);
snum=ceil(datalength/period);
for(i=1:snum-1)
data2((i-1)*period+1:(i-1)*period+period)=encoded_data((i-1)*period+1:(i-1)*period+period)+sigma*randn(1,period);
end
data2((snum-1)*period+1:datalength)=encoded_data((snum-1)*period+1:datalength)+sigma*randn(1,length(encoded_data((snum-1)*period+1:datalength)));
rec_data2=zeros(1,nwords*n);
for i=1:nwords*n
if abs(encoded_data(i)-data2(i))>0.5
rec_data2(i)=xor(encoded_data(i),1);
else
rec_data2(i)=encoded_data(i);
end
end
rec_data2=gf(rec_data2,m);
%BCH譯碼
for j=1:nwords
rec_data=rec_data2((j-1)*n+1:(j-1)*n+n);
syndrome=gf(zeros(1, 2*t), m);
for i=1:n,
syndrome=syndrome.*alpha_tb+rec_data(n-i+1);
end;
lambda = gf([1, zeros(1, t)], m);
lambda0= lambda;
b=gf([0, 1, zeros(1, t)], m);
b2 = gf([0, 0, 1, zeros(1, t)], m);
k1=0;
gamma = one;
delta = zero;
syndrome_array = gf(zeros(1, t+1), m);
if(simplified == 1)
for r=1:t,
r1 = 2*t-2*r+2;
r2 = min(r1+t, 2*t);
num = r2-r1+1;
syndrome_array(1: num) = syndrome(r1:r2);
delta = syndrome_array*lambda';
lambda0 = lambda;
lambda = gamma*lambda-delta*b2(2:t+2);
if((delta~= zero) && (k1>=0))
b2(3)=zero;
b2(4:3+t) = lambda0(1:t);
gamma = delta;
k1 = -k1;
else
b2(3:3+t) = b2(1:t+1);
gamma = gamma;
k1=k1+2;
end
joke=1;
end
else
for r=1:2*t,
r1 = 2*t-r+1;
r2 = min(r1+t, 2*t);
num = r2-r1+1;
syndrome_array(1:num) = syndrome(r1:r2);
delta = syndrome_array*lambda';
lambda0 = lambda;
lambda = gamma*lambda-delta*b(1:t+1);
if((delta ~= zero) && (k1>=0))
b(2:2+t)=lambda0;
gamma = delta;
k1=-k1-1;
else
b(2:2+t) = b(1:t+1);
gamma = gamma;
k1=k1+1;
end
joke=1;
end
end
inverse_tb = gf(zeros(1, t+1), m);
for i=1:t+1,
inverse_tb(i) = alpha^(-i+1);
end;
%錢搜尋法
lambda_v = zero;
accu_tb=gf(ones(1, t+1), m);
for i=1:n,
lambda_v=lambda*accu_tb';
accu_tb = accu_tb.*inverse_tb;
if(lambda_v==zero)
error(1,n-i+1)=1;
else
error(1,n-i+1)=0;
end
end
found = find(error(1,:)~=0);
for i=1:length(found)
location=found(i);
if location <= k;
rec_data(n-location+1)=rec_data(n-location+1)+one;
end
end
decoded_data((j-1)*k+1:(j-1)*k+k)=rec_data(n-k+1:n);
end
·訊雜比模擬
clc;
clear all;
close all;
%引數設定%(511,493)(4095.4035)
givenSNR=0.5:0.5:9.5; %]
% N=511;
% K=493;
N=4095;
K=4035;
T=11;
times=length(givenSNR);
%計算幾個值
r=K/N;
Eb_N0=10.^(givenSNR./10);
sigma=(1./(2*r.*Eb_N0).^0.5);
message=randint(times,K,[0,1]);
msg=gf(message);
BCHcode_gf=bchenc(msg,N,K);
%BCH編碼
BCHcode_double=-1*ones(times,N);
for code_i=1:times
for code_j=1:N
if BCHcode_gf(code_i,code_j)==1
BCHcode_double(code_i,code_j)=1;
end
end
end
%新增噪聲
for noise_i=1:length(sigma)
BCH_receive(:,:,noise_i)=BCHcode_double+sigma(noise_i)*randn(times,N);
end
for noise_i=1:length(sigma)
for hard_i=1:times
for hard_j=1:N
if BCH_receive(hard_i,hard_j,noise_i)>0
hard_coded(hard_i,hard_j,noise_i)=1;
end
end
end
end
%BCH解碼
BCHdecode=gf(zeros(times,K,length(sigma)));
for noise_i=1:length(sigma)
hard_BCH=hard_coded(:,:,noise_i);
[BCHdecode_i,error_num]=bchdec(gf(hard_BCH),N, K);
BCHdecode(:,:,noise_i)=BCHdecode_i;
end
BCHdecode_double=zeros(times,K);
for noise_i=1:length(sigma)
for gf_to_double_i=1:times
for gf_to_double_j=1:K
if BCHdecode(gf_to_double_i,gf_to_double_j,noise_i)==1
BCHdecode_double(gf_to_double_i,gf_to_double_j,noise_i)=1;
end
end
end
end
for noise_i=1:length(sigma)
error_BCHcoded_num(noise_i)=sum(sum((abs(BCHdecode_double(:,:,noise_i)-message))));
end
coded_error_rate=error_BCHcoded_num/times/K
semilogy(givenSNR,coded_error_rate,'-*');
ylabel('BER');
xlabel('Eb/N0');
grid on;