前言

雙線性插值與雙線性取樣是在影象插值和取樣過程中常用的操作，在pytorch中對應的函數是torch.nn.functional.grid_sample，本文對該操作的原理和程式碼例程進行筆記。如有謬誤，請聯絡指正，轉載請聯絡作者並註明出處，謝謝。

$\nabla$ 聯絡方式：

e-mail: FesianXu@gmail.com

QQ: 973926198

github: https://github.com/FesianXu

知乎專欄: 計算機視覺/計算機圖形理論與應用

---

雙線性插值原理

插值（interpolation）在數學上指的是 一種估計方法，其根據已知的離散資料點去構造新的資料點。以曲線插值為例子，如Fig 1.1所示的曲線線性插值為例，其中紅色資料點是已知的資料點，而藍色線是根據相鄰的兩個紅色資料點進行線性插值估計出來的。

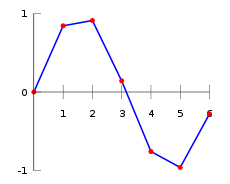
一維的曲線插值的原理可以推廣到任意維度的資料形式上，比如我們常見的影象是一種二維資料，就可以進行二維插值，常見的插值方法如Fig 1.2所示。

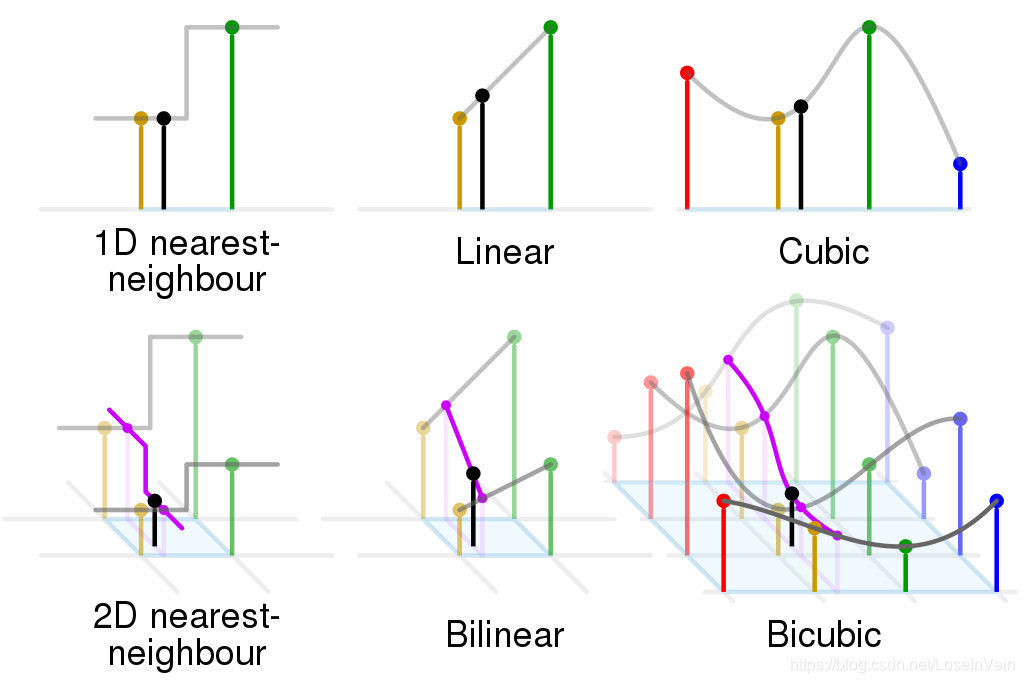
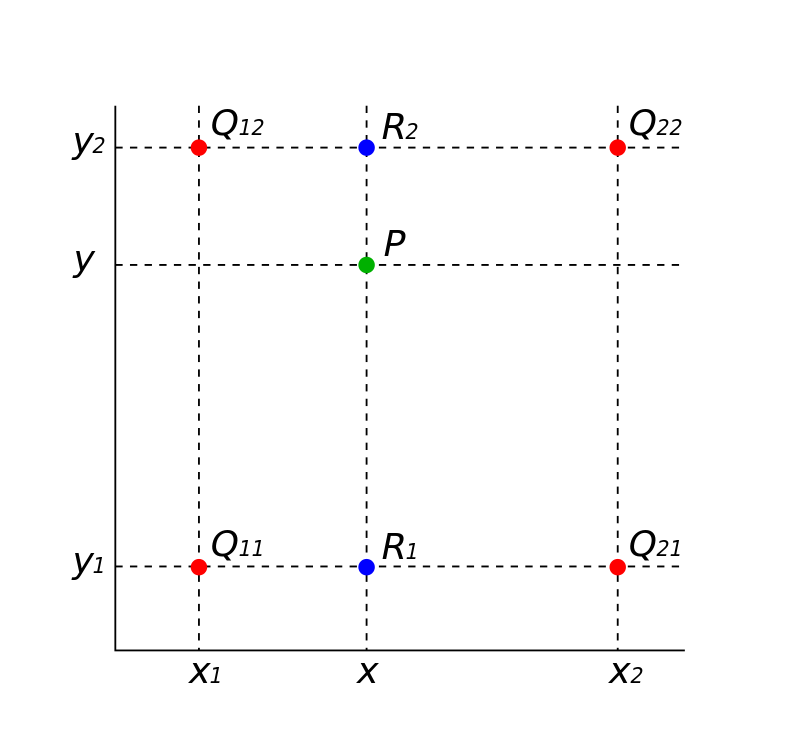
在本文中，我們主要討論的是雙線性取樣，而雙線性取樣和雙線性插值緊密相關，因此本章節主要介紹雙線性插值。還是以2D影象插值為例子，如Fig 1.3所示，假設圖片上給定了紅色資料點的畫素值，假設待求的綠色點$P=(x,y)$，其中已知每個頂點畫素座標為：
$$\begin{array}{rl}{Q}_{12}& =(x_1,y_2{)}^{\mathrm{T}}\\ Q_{22}& =(x_2,y_2{)}^{\mathrm{T}}\\ Q_{11}& =(x_1,y_1{)}^{\mathrm{T}}\\ Q_{21}& =(x_2,y_1{)}^{\mathrm{T}}\end{array}\text{\hspace{1em}(1.1)}$$
而每個頂點的畫素值表示為$f(Q_{ij}),i=1,2,j=1,2$。通過簡單的線性插值（按比例劃分），我們可以求出藍色資料點的估計值：
$$\begin{array}{rl}{R}_2& =f(x,y_2)=\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})\\ R_1& =f(x,y_1)=\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})\end{array}\text{\hspace{1em}(1.2)}$$
然後通過藍色點，再一次進行線性插值，可以估計出綠色點的值：
$$\begin{array}{rl}f(x,y)& =\frac{y_2-y}{y_2-y_1}f(x,y_1)+\frac{y-y_1}{y_2-y_1}f(x,y_2)\\ & =\frac{1}{(x_2-x_1)(y_2-y_1)}[x_2-x,x-x_1]\left[\begin{array}{cc}f(Q_{11})& f(Q_{12})\\ f(Q_{21})& f(Q_{22})\end{array}\right]\left[\begin{array}{c}{y}_2-y\\ y-y_1\end{array}\right]\end{array}\text{\hspace{1em}(1.3)}$$

因為該方法涉及到了兩輪（注意不是兩次，而是三次）的線性插值，因此稱之為雙線性插值（Bilinear Interpolation）。

雙線性取樣以及grid_sample

在深度學習框架pytorch中提供了一種稱之為雙線性取樣（Bilinear Sample）的函數torch.nn.functional.grid_sample [1]，該函數主要輸入一個形狀為$(N,C,H_{in},W_{in})$的input張量，輸入一個形狀為$(N,H_{out},W_{out},2)$的grid張量，輸出一個形狀為$(N,C,H_{out},W_{out})$的output張量。

其中$N$為batch批次，我們主要關注後面的維度的代表意義。輸入的grid是一個$H_{out}\times W_{out}$大小的空間位置矩陣，其中每個元素都代表著一個二維空間座標$(x,y)$，該座標指明瞭在input上取樣的座標，而輸出張量的每個位置output[n,:,h,w]的值，取決於這個輸入input和取樣座標的值（通過雙線性插值形成）。通過這個函數，可以通過指定原圖的不同座標位置，實現圖片的變形（deformation）等，在很多研究中有著廣泛地應用[2]。

注意到這裡的輸出張量尺寸和輸入張量尺寸是不一定一致的，因此涉及到了插值過程，而且輸入的grid的每一個座標都是歸一化到了$[-1,1]$之間的，我們舉一個簡單的程式碼例子，明晰下細節。

import torch.nn.functional as F
import torch
inputv = torch.arange(4*4).view(1, 1, 4, 4).float()
print(inputv)
'''
輸出尺寸為(1,1,4,4)
輸出為：tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
'''
# 生成grid，這個grid大小為(1,8,8,2)，空間尺寸而言是原輸入圖片的兩倍。
d = torch.linspace(-1,1, 8)
meshx, meshy = torch.meshgrid((d, d))
grid = torch.stack((meshy, meshx), 2)
grid = grid.unsqueeze(0) # add batch dim

# 進行雙線性取樣，其中指定align_corners=True保證了輸出的整個圖片的角邊畫素與原輸入的一致性。
output = F.grid_sample(inputv, grid,align_corners=True)
print(output)
'''
tensor([[[[ 0.0000,  0.4286,  0.8571,  1.2857,  1.7143,  2.1429,  2.5714,
            3.0000],
          [ 1.7143,  2.1429,  2.5714,  3.0000,  3.4286,  3.8571,  4.2857,
            4.7143],
          [ 3.4286,  3.8571,  4.2857,  4.7143,  5.1429,  5.5714,  6.0000,
            6.4286],
          [ 5.1429,  5.5714,  6.0000,  6.4286,  6.8571,  7.2857,  7.7143,
            8.1429],
          [ 6.8571,  7.2857,  7.7143,  8.1429,  8.5714,  9.0000,  9.4286,
            9.8571],
          [ 8.5714,  9.0000,  9.4286,  9.8571, 10.2857, 10.7143, 11.1429,
           11.5714],
          [10.2857, 10.7143, 11.1429, 11.5714, 12.0000, 12.4286, 12.8571,
           13.2857],
          [12.0000, 12.4286, 12.8571, 13.2857, 13.7143, 14.1429, 14.5714,
           15.0000]]]])
'''

在這個過程中，我們生成的取樣座標網格grid很簡單，單純只是在x,y兩個維度，都把$[-1,1]$均分為了8份。

我們分析下雙線性取樣後的每個畫素的大小計算過程。因為每個輸入座標都是$[-1,1]$，而實際原輸入的矩陣大小為$[0,3]$，而且剛好是一個方陣，因此可以計算出從grid到實際座標的對映為:
$$f_x=f_y=\frac{3}{2}{x}_{norm}+\frac{3}{2}\text{\hspace{1em}(1)}$$
這個對映將歸一化座標對映到了實際的原圖座標，如果不是方陣，那麼就必須對$x,y$每個維度都計算一個對映方程。

我們暫時只考慮怎麼計算其中某一個畫素的值，暫時我們考慮grid座標為$[1,1]$的值。我們列印出grid[0,1,1,:]，發現這個歸一化座標值為tensor([[-0.7143, -0.7143]])，那麼通過反歸一化對映，也就是式子(1)後，有實際圖片座標為$(0.4285,0.4285)$，這個時候我們發現這個座標不是整數，因此為了求出這個座標的畫素值，我們要通過之前談到的雙線性插值去估計。

首先求出每一行的插值結果，有$f(x,y_1)=0.4285$，這個是在$[0,1]$中插值的結果；有$f(x,y_2)=4.4285$這個是在$[4,5]$範圍內插值的結果，然後再在$[0.4285,4.4285]$中進行插值，有$f(x,y)=(4.4285-0.4285)\times 0.4285+0.4285=2.1428$。這就是整個雙線性取樣的計算過程。

注意：這個輸入input也可以是$(N,C,D,H_{in},W_{in})$的5D輸入，該輸入考慮的是對視訊進行處理。本文中只考慮了圖片資料，不過原理是類似的，不再贅述。

Reference

[1]. https://pytorch.org/docs/stable/nn.functional.html#torch.nn.functional.grid_sample

[2]. https://blog.csdn.net/LoseInVain/article/details/108710063