緒論

數位影像處理方法的重要性源於兩個主要應用領域：改善圖示資訊以便人們解釋；為儲存、傳輸和表示而對影象資料進行處理，以便機器自動理解。

---

1、數位影像

自然界中的影象都是模擬量，在計算機普遍應用之前，電視、電影、照相機等影象記錄與傳輸裝置都是使用模擬訊號對影象進行處理。但是，計算機只能處理數位量，而不能直接處理模擬影象。所以我們要在計算機處理影象之前進行影象數位化處理。

1.1、什麼是數位影像

簡單的說，數位影像就是能夠在計算機上顯示和處理的影象，可根據其特徵分為兩大類——點陣圖和向量圖。點陣圖通常使用數位陣列來表示，常見的格式有 BMP、JPG、GIF 等；向量圖由向量資料庫表示，我們接觸最多的就是 PNG 圖形。

一幅影象可定義為一個二維函數 f(x,y)，其中 x 和 y 是空間（平面）座標，而在任何一對空間座標（x,y）處的幅值 f 稱為影象在該點處的強度、亮度或灰度。當 x,y 和灰度值 f 是非負有限的離散數值時，我們稱該影象為數位影像（點陣圖）。

注意，數位影像處理是由有限數量的元素組成，每個元素都有一個特定的位置和幅值。這些元素稱為圖畫元素、影象元素或畫素。畫素是廣泛用於表示數位影像元素的術語。例如，一個大小為 M×N 數位影像是由 M 行 N 列的有限元素組成，每個元素都有特定的位置和幅值，代表了其所在行列位置上的影象物理資訊，如灰度和色彩等。這些元素稱為影象元素或畫素。

1.2、數位影像的顯示

不論是 CRT 顯示器還是 LCD 顯示器，都是由許多點構成，顯示影象時這些點對應著影象的畫素，稱顯示器為位映像裝置。所謂位映像裝置，就是一個二維的畫素矩陣，而點陣圖也就是採用位映像方法顯示和儲存的影象。當一幅數位影像被放大後就可以明顯地看出影象是由很多的方格形狀的畫素構成的。

1.3、數位影像的分類

根據每個畫素所代表的資訊的不同，可將影象分為二值影象、灰度影象、RGB 影象以及索引影象等。

1.3.1、二值影象

每個畫素只有黑、白兩種顏色的影象稱為二值影象。在二值影象中，畫素只有 0 和 1 兩種取值，一般用 0 來表示黑色，用 1 表示白色。

1.3.2、灰度影象

在二值影象中進一步加入許多介於黑色與白色之間的顏色深度，就構成了灰度影象。這類影象通常顯示為從最暗黑色到最亮的白色的灰度，每種灰度（顏色深度）稱為一個灰度級，通常用 L 來表示。在灰度影象中，畫素可以取 0~L-1 之間的整數值，根據儲存灰度值所使用的資料型別的不同，可能有 256 種取值或者說 2^k 種取值，當 k=1 時即退化為二值影象。

1.3.3、RGB 影象

眾所周知，自然界中幾乎所有顏色都可以由紅（Red，R）、綠（Green，G）、藍（Blue，B）3 種顏色組合而成，通常稱它們為 RGB 三原色。計算機顯示彩色影象時採用最多的就是 RGB 模型，對於每個畫素，通過控制 R、G、B 三原色的合成比例決定該畫素的最終顯示顏色。

對於三原色 RGB 中的每一種顏色，可以像灰度圖那樣使用 L 個等級來表示含有這種顏色成分的多少。例如對於含有 256 個等級的紅色，0 表示不含紅色成份，255 表示含有 100% 的紅色成份。同樣，綠色和藍色也可以劃分為 256 個等級。這樣每種原色可以用 8 位二進位制資料表示，於是三原色總共需要 24 位二進位制數，這樣能夠表示出的顏色種類數目為 256×256×256=2^24，大約有 1600 萬種，已經超過了普通人所能分辨出的顏色數目。

RGB 顏色程式碼可以使用十六進位制數減少書寫長度，按照兩位一組的方式依次書寫 R、G、B 三種顏色的級別。例如，0xFF0000 代表純紅色，0x00FF00 代表純綠色，而 0x00FFFF 是青色。常見顏色的 RGB 組合值的表如下：

顏色	R	G	B
紅（0xFF0000）	255	0	0
藍（0x00FF00）	0	255	0
綠（0x0000FF）	0	0	255
黃（0xFFFF00）	255	255	0
紫（0xFF00FF）	255	0	255
青（0x00FFFF）	0	255	255
白（0xFFFFFF）	255	255	255
黑（0x000000）	0	0	0
灰（0x808080）	128	128	128

未經壓縮的原始 BMP 檔案就是使用 RGB 標準給出的 3 個數值來儲存影象資料的，稱為 RGB 影象。在 RGB 影象中每個畫素都是用 24 位二進位制數表示，故也稱為 24 位真彩影象。

1.3.4、索引影象

如果對每個畫素直接使用 24 位二進位制數表示，影象檔案的體積將變得十分龐大。來看一個例子，對一個長、寬各為 200 畫素，顏色數為 16 的彩色影象，每個畫素都用 RGB 3 個分量表示。這樣每個畫素由 3 位元組表示，整個影象就是 200×200×3=120KB。這種未經壓縮的表示方法浪費了大量的儲存空間。所以就引出了另一種更為節省空間的儲存方式：索引影象。

同樣是對 200×200 畫素的 16 色影象，由於這張影象最多隻有 16 種顏色，那麼可以用一張顏色表（16×3 的二維陣列）儲存這 16 種顏色對應的 RGB 值，在表示影象的矩陣中使用那 16 種顏色在顏色表中的索引（偏移量）作為資料寫入相應的行列位置。這樣一來，每一個畫素所需要使用的二進位制數就僅僅為 4 位（0.5 位元組），從而整個影象只需要 200×200×0.5 = 20KB 就可以儲存。

上文所提到的顏色表就是常說的調色盤（Palette），另一種說法叫做顏色查詢表（LUT：Look Up Table）。

1.4、數位影像的實質

更嚴格地說，數位影像可以是兩個變數（對於靜止影象）或 3 個變數（對於動態影象）的離散函數。在靜態影象的情況下是 f(x,y)，而如果是動態影象畫面，則還需要時間引數 t，即 f(x,y,t)；函數值可能是一個數值（對於灰度影象），也可能是一個向量（對於彩色影象）。

影象處理是一個涉及諸多領域的交叉學科，下面從不同的角度來審視數位影像：

• 從線性代數和矩陣論的角度，數位影像是由影象資訊組成的二維矩陣，矩陣的每個元素代表對應位置上的影象亮度和/或色多媒體簡訊息。當然，這個二維矩陣在資料表示和儲存上可能不是二維的，這是因為每個單位位置的影象資訊可能需要不只一個數值來表示，這樣可能需要一個三維矩陣來對其進行表示。
• 由於隨機變化和噪聲的原因，影象在本質上是統計性的。因而有時將影象作為隨機過程的實現來觀察存在其優越性。這時有關影象資訊量和冗餘的問題可以用概率分佈和相關函數來描述。例如，可以用熵 H 來度量影象的資訊量。
• 從線性系統的角度考慮，影象及其處理也可以表示為用狄拉克衝激公式表達的點展開函數的疊加，在使用這種方式對影象進行表示時，可以採用成熟的線性系統理論研究。

1.5、數位影像的表示

為了表述畫素之間的相對和絕對位置，我們通常還需要對畫素的位置進行座標的約定。

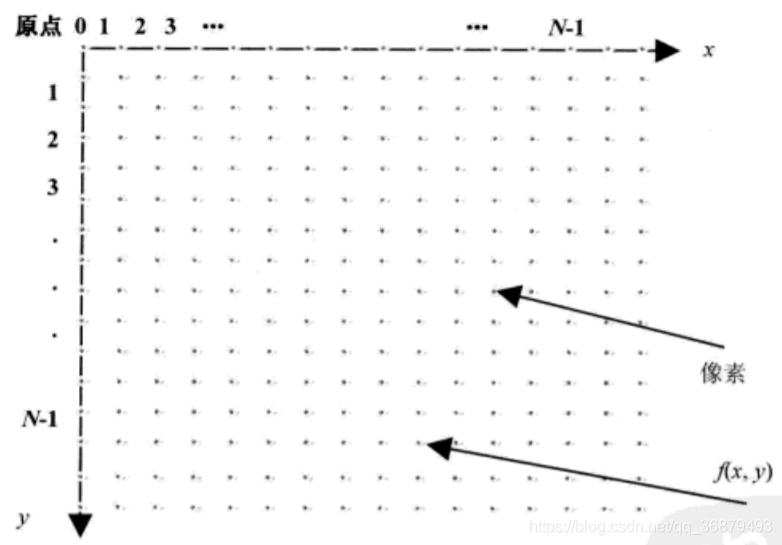
在這之後，一幅物理圖就被轉換成了數位矩陣，從而成為計算機能夠處理的物件了。數位影像 f 的矩陣表示如下：
$$f(y,x)=\left[\begin{array}{ccc}f(0,0)& \cdots & f(0,N-1)\\ ⋮& \cdots & ⋮\\ f(M-1,0)& \cdots & f(M-1,N-1)\end{array}\right]$$
也可以使用傳統的矩陣表示法來表示數位影像和畫素。

其中行列（M 行 N 列）必須是正整數，而離散灰度級數目 L 一般為 2 的 k 次冪，k 為整數（因為使用二進位制整數值來表示灰度值），影象的動態範圍為 [0,L-1]，那麼影象儲存所需的位元數為 b = M×N×k。

1.6、影象的空間和灰度級解析度

1.6.1、影象的空間解析度

影象的空間解析度是指影象中每單位長度所包含的畫素或點的數目，常以**畫素/英寸（ppi）**為單位來表示。如：72ppi 表示影象中每英寸包含 72 個畫素或點。解析度越高，影象越清晰，影象檔案所需的磁碟空間也越大，編輯和處理所需的時間也越長。

畫素越小，單位長度所包含的畫素資料就越多，解析度也就越高，但同樣物理大小範圍內所對應影象的尺寸也會越大，儲存影象所需要的位元組數也越多。因而，在影象的放大縮小演演算法中，放大就是對影象的過取樣，縮小就是對影象的欠取樣。

1.6.2、影象的灰度級/輻射計量解析度

在數位影像處理中，灰度級解析度又稱為色階，是指影象中可分辨的灰度級數目，即前面提到的灰度級數目 L，它與儲存灰度級別所使用的資料型別有關。由於灰度級度量的是投射到感測器上的光輻射值的強度，所以灰度級解析度也叫輻射計量解析度。

隨著影象的灰度級解析度逐漸降低，影象中包含的顏色數目變少，從而在顏色的角度造成影象資訊受損，同樣使影象細節表達受到一定影響。

---

2、數位影像處理與識別

2.1、從影象處理到影象識別

2.1.1、數位影像處理

數位影像處理（Digital Image Processing）就是指使用電子計算機對量化的數位影像進行處理，具體地說就是通過影象進行各種加工來改善影象的外觀，是對影象的修改和增強。

影象處理的輸入是從感測器或其他來源獲取的原始的數位影像，輸出的是經過處理後的輸出影象。處理的目的可能是使輸出的影象具有更好的效果，以便於人的觀察；也可能是為影象分析和識別做準備，此時的影象處理是作為一種預處理步驟，輸出的影象將進一步供其他影象分析、識別演演算法使用。

2.1.2、數位影像分析

數位影像分析（Digital Image Analyzing）是指對影象中感興趣的目標進行檢測和測量，以獲得客觀的資訊。數位影像分析通常是指將一幅影象轉換為另一種非影象的抽象形式，如圖中某物體與測量者的距離以及目標物件的計數或其尺寸等。這一概念的外延包括邊緣檢測和影象分割、特徵提取以及幾何測量與計數等。

影象分析的輸入是經過處理的數位影像，其輸出通常不再是數位影像，而是一系列與目標相關的影象特徵（目標的描述），如目標的長度、顏色、曲率和個數等。

2.1.3、數位影像識別

數位影像識別（Digital Image Recognition）主要研究影象中各目標的性質和互相關係，識別出目標物件的類別，從而理解影象的含義。

影象識別是影象分析的延伸，它根據從影象分析中得到的相關描述（特性）對目標進行歸類，輸出我們感興趣的目標類別標號資訊（符號）。

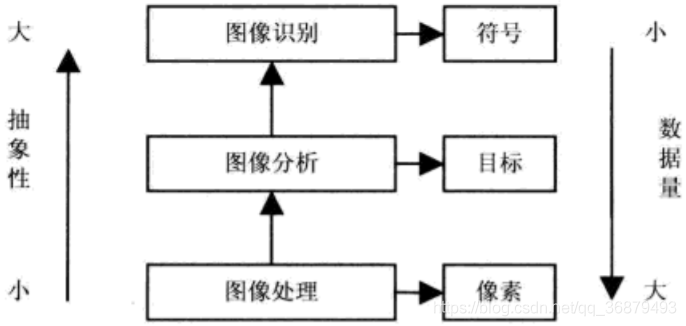
總的來說，從影象處理到影象分析再到影象識別這個過程，是一個將所含資訊抽象化，嘗試降低資訊熵，提煉有效資訊的過程。

2.2、數位影像處理與識別的應用範例

相關領域	典型應用
安全監控	指紋驗證，基於臉部辨識的門禁系統
工業控制	產品無失真檢測，商品自動分類
醫療保健	X 光照片增強，CT，核磁共振，病灶自動檢測
生活娛樂	基於表情識別的笑臉自動檢測，汽車自動駕駛，手寫字元識別

2.3、數位影像處理與識別的基本步驟

• 影象的點運算通過灰度變換可有效改善影象的外觀，並在一定程度上實現影象的灰度歸一化。有很多基於影象點運算的處理方法，如影象拉伸、對比度增強、直方圖均衡以及直方圖匹配等。
• 影象的幾何變換主要應用在影象的幾何歸一化和影象校準當中。
• 影象增強，可理解為根據特定的需求突出一幅影象中的某些資訊，同時削弱或去掉某些不需要的資訊的處理方法。其主要目的是使處理後的影象對某種特定的應用來說，比原始影象更適用。作為影象處理中一個相當主觀的領域，影象增強是以下多種影象處理方法的前提和基礎，也是在影象獲取後的先期步驟。
• 小波變換伴隨著人們對影象壓縮、邊緣和特徵檢測以及紋理分析的需求的提高應運而生。傅立葉變換一直是頻率域影象處理的基石，它能用正弦函數之和表示任何分析函數，而小波變換則基於一些有限寬度的基小波，這些小波不僅在頻率上是變化的，而且具有有限的持續時間。
• 影象復原與影象增強類似，其目的是改善影象品質。但是影象復原是試圖利用退化過程的先驗知識使已被退化的影象恢復本來面目，而影象增強是用某種試探的方式改善影象品質，以適應人眼的視覺與心理。引起影象退化的因素包括由光學系統、運動等造成的影象模糊，以及源自電路和光學因素的噪聲等。影象復原是基於影象退化的數學模型，復原的方法也建立在比較嚴格的數學推導上。
• 彩色影象處理實際上從影象的型別分類，主要包括對全綵影象的處理，也包括灰度影象的偽彩色化。更復雜。
• 形態學影象處理是一種將數學形態學推廣應用於影象處理領域的新方法，是一種基於物體自然形態的影象處理分析方法。而形態學的概念最早起源於生物學，是一門生物學中研究動物和植物結構的一個分支科學。數學形態學（也稱為影象代數）則是一種以形態為基礎對影象進行分析的數學工具，其基本思想是用具有一定形態的結構元素去度量和提取影象中的對應形狀以達到對影象分析和識別的目的。影象形態學往往用於邊界提取、區域填充、連通分量的提取、凸殼、細化、畫素化等影象操作。
• 影象分割是指將一幅影象分解為若干個互不交疊區域的過程，分割出來的區域需要同時滿足均勻性和連通性的條件。目標的表示與描述是指目標區域的畫素或區域邊界的畫素標出這一目標，並且對目標進行抽象描述，使計算機能充分利用所獲得的處理分割結果。
• 特徵提取指的是進一步處理之前得到的影象區域和邊緣，使其成為一種更適合於計算機處理的形式。我們研究如何從影象中提取有用的資料或資訊，得到的影象的 「非影象」 的表示或描述，如數值、向量和符號等，這一過程就是特徵提取，而提取出來的這些 「非影象」 的表示或描述就是特徵。有了這些數值或向量形式特徵我們就可以通過訓練過程教會計算機如何懂得這些特徵，從而使計算機具有了識別影象的本領。常用的影象特徵有：紋理特徵、形狀特徵、空間關係特徵等。
• 物件識別一般是指利用前一步從數位影像中提取的特徵向量進行分類和理解的過程，這涉及計算機技術、圖形識別、人工智慧等多方面的知識。這一步驟建立在前面諸多步驟之上，用以向上層控制演演算法提供最終所需的資料或直接報告識別結果。事實上，物件識別已經上升到機器視覺的層面了。

---

3、數位影像處理的預備知識

3.1、鄰接性、連通性、區域和邊界

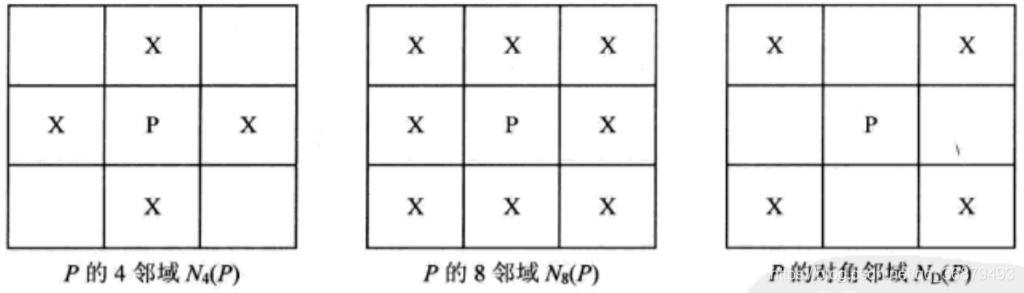
相鄰畫素的概念。依據標準的不同，我們關注畫素 P 的 4 鄰域和 8 鄰域：

3.1.1、鄰接性

定義 V 是用於決定鄰接性的灰度值集合，它是一種相似性的度量，用於確定所需判斷鄰接性的畫素之間的相似程度。

例如在二值影象中，如果我們認為只有灰度值為 1 的畫素是相似的，則即 V = {1}，當然相似性的規定具有主觀標準，因此也可以認為 V = {0,1}，此時鄰接性完全由位置決定；而對於灰度影象，這個集合中則很可能包含更多的元素。此外，定義對角鄰接域 ND§ 為 8-鄰域中不屬於 4-鄰域的部分，那麼：

• 4 鄰接：如果
  $$Q\in N_4(P)$$
  則稱具有 V 中數值的兩個畫素 P 和 Q 是4 鄰接的。

• 8 鄰接：如果
  $$Q\in N_8(P)$$
  則稱具有 V 中數值的兩個畫素 P 和 Q 是 8 鄰接的。

舉例來說，下圖分別是畫素和 Q、Q1、Q2 的 4 鄰接和 8 鄰接示意圖。而對於兩個影象子集 S1 和 S2，如果 S1 中的某些畫素和 S2 中的某些畫素相鄰，則稱這兩個子集是鄰接的。

3.1.2、連通性

畫素的通路 畫素 P 到畫素 Q 的通路（Path） 指的是一個特定的畫素序列 (x0,y0),(x1,y1),…,(xn,yn)，其中 (x0,y0) = (xp,yp)，(xn,yn) = (xq,yq)。並且畫素 (xi,yi) 和 (xi-1,yi-1) 在滿足 1<= i <= n 時是鄰接的。通過上面的定義，n 是通路的長度，若 (x0,y0) = (xn,yn)，則稱這條通路是閉合通路。

畫素的連通性 令 S 代表一幅影象中的畫素子集。如果在 S 中全部畫素之間存在一個通路，則可以稱兩個畫素 P 和 Q 在 S 中是連通的。此外，對於 S 中的任何畫素 P，S 中連通到該畫素的畫素集叫做 S 的連通分量。如果 S 中僅有一個連通分量，則集合 S 叫做連通集。

3.1.3、區域和邊界

**區域（Region）**的定義是建立在連通集的基礎上的。

區域 如果 R 同時是連通集，則稱 R 為一個區域（Region）。

**邊界（Boundary）**的概念是相對於區域而言的。

邊界 一個區域的邊界（或邊緣、輪廓）是區域中所有有一個或多個不在區域 R 中的鄰接畫素的畫素所組成的集合。

顯然，如果區域 R 是整幅影象，那麼邊界就由影象的首行、首列、末行和末列定義。通常情況下，區域指的是一幅影象的子集，幷包括區域的邊緣。而區域的邊緣（Edge）由具有某些導數值的畫素組成，是一個畫素及其直接鄰域的區域性性質，是一個有大小和方向屬性的向量。

邊界和邊緣是不同的。邊界是和區域有關的向量，而邊緣表示的影象函數的區域性性質。

3.2、距離度量的幾種方法

假設對於畫素 P(xp,yp)，Q(xq,yq)，R(xr,yr) 而言，有函數 D 滿足如下 3 個條件，則函數 D 可被稱為距離函數或度量。

1. D(P,Q) >= 0，當且僅當 P = Q 時有 D(P,Q) = 0；
2. D(P,Q) = D(Q,P)；
3. D(P,Q) <= D(P,R) + D(R,Q)。

常見的幾種距離函數如下：

• 歐式距離
  $$D_e(P,Q)=\sqrt{{\left(x_p-x_p\right)}^2+{\left(y_p-y_p\right)}^2}$$

​ 即距離等於 r 的畫素形成以 P 為圓心的圓。

• D4 距離（街區距離）
  $$D_4(P,Q)=\left|x_p-x_q\right|+\left|y_p-y_q\right|$$
  即距離等於 r 的畫素形成以 P 為中心的菱形。

• D8 距離（棋盤距離）
  $$D_8(P,Q)=\max \left(\left|x_p-x_q\right|+\left|y_p-x_q\right|\right)$$
  即距離等於 r 的畫素形成以 P 為中心的方形。

3.3、基本的影象操作

按照處理影象的數量分類，可以分為對單幅影象操作（如濾波）和對多幅影象的操作（如求和、求差和邏輯運算等）；按照參與操作的畫素範圍的不同，可以分為點運算和鄰域運算；而根據操作的數學性質，又可分為線性操作和非線性操作。