刷爆朋友的圈的面試題?位元組跳動編碼題解析思路分享!
前言:
臨近國慶節,自己的一個小圈子微信群的夥伴們發了一張圖片,是網上流傳的位元組跳動的面試題編碼,閒的無事就思索了下,發現都不難,都是對基礎的數學知識的考量。先上圖吧!
當然40分鐘,我也無法把任意兩題編碼完成,只是知道大概的解題思路,唯一能確定的,在面試規定時間內,第二題我是肯定可以在20分鐘內編碼完成。

正題
題目一
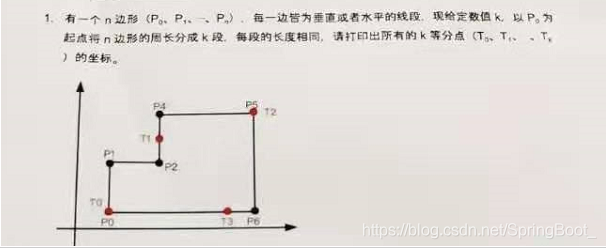
基礎知識就是初中的平面直角座標系,解析思路:
- 計算總周長;
- 將各邊長的前後座標計算出來封裝好,第四步要使用;
- 根據K段值計算出平均分段後的長度;
- 然後迴圈K次,根據平均長度依次相加計算等分點的座標。
不多說,上程式碼:
先定義座標的Point類
class Point {
float x;
float y;
public Point() {
}
public Point(float x, float y) {
this.x = x;
this.y = y;
}
public Point(Point point) {
this(point.x, point.y);
}
@Override
public String toString() {
return "Point, x:" + x + " y:" + y;
}
}
N邊形的邊封裝類
class Line {
Point begin;
Point end;
float length;
public Line() {
}
public Line(Point begin, Point end, float length) {
this.begin = begin;
this.end = end;
this.length = length;
}
}
現在上實現計算的類
這段程式碼第一個版本的時候,在正方形偶數等分的時候,座標點計算不準確,今晚上看著程式碼思考了10分鐘的樣子,稍微改動了下,暫時沒有這個bug了。其他的bug,期待大家一起發現,然後修復吧!
public class Polygon {
/**
* 計算邊的長度
*
* @return
*/
private static float lineLength(Point a, Point b) {
float length;
if (a.x == b.x) {
// 垂直線條
length = Math.abs(a.y - b.y);
} else {
length = Math.abs(a.x - b.x);
}
return length;
}
/**
* 計算 周長
*
* @return
*/
private static float totalSideLength(Point[] points, Line[] lines) {
float side = 0;
for (int i = 1; i < points.length; i++) {
Point prev = points[i - 1];
Point point = points[i];
float length = lineLength(prev, point);
side += length;
lines[i - 1] = new Line(prev, point, length);
if (i == points.length - 1) {
length = lineLength(point, points[0]);
side += length;
lines[i] = new Line(point, points[0], length);
}
}
return side;
}
public static Point[] division(Point[] points, int divisionNum) {
Point[] divisionPoint = new Point[divisionNum];
// 計算周長
Line[] lines = new Line[points.length];
float side = totalSideLength(points, lines);
// 等分長度
float divisionLength = side / divisionNum;
int lineIndex = -1;
float sumLength = 0;
for (int i = 0; i < divisionNum; i++) {
if (i == 0) {
// 第一個等分點直接是起始點座標
divisionPoint[i] = new Point(points[0]);
continue;
}
divisionPoint[i] = new Point();
float lineLength = divisionLength * i;
while (true) {
Line line;
if (sumLength < lineLength) {
lineIndex++;
line = lines[lineIndex];
sumLength += line.length;
} else
line = lines[lineIndex];
if (sumLength >= lineLength) {
float temp = sumLength - lineLength;
if (line.begin.x == line.end.x) {
// begin和end的座標點垂直
divisionPoint[i].x = line.begin.x;
if (line.end.y > line.begin.y)
divisionPoint[i].y = line.end.y - temp;
else
divisionPoint[i].y = line.end.y + temp;
} else {
// begin和end的座標點水平
divisionPoint[i].y = line.end.y;
if (line.end.x > line.begin.x)
divisionPoint[i].x = line.end.x - temp;
else
divisionPoint[i].x = line.end.x + temp;
}
break;
}
}
}
return divisionPoint;
}
private static void print(Point[] points) {
for (int i = 0; i < points.length; i++) {
System.out.println("第" + (i + 1) + "等分點, x:" + points[i].x + ",y:" + points[i].y);
}
}
public static void main(String[] args) {
Point[] points = new Point[] { new Point(0, 0), new Point(0, 1), new Point(1, 1), new Point(1, 0) };
Point[] divPoints = division(points, 8);
print(divPoints);
}
}
題目二

解題思路:
對應位數的數位相加,永遠不會超過18,所以,我們就先把對應位置的和計算出來,然後再反覆迴圈找到大於9的數,向高位進位。
這個比較簡單,只是考察個位數的正整數加法永遠不大於18這個細節。
上程式碼:
public class LinkAddition {
static class NumNode {
public int num;
public NumNode next;
public NumNode() {
}
public NumNode(int num) {
this.num = num;
};
public NumNode(int num, NumNode next) {
this(num);
this.next = next;
}
}
private static int length(NumNode num) {
int length = 0;
NumNode temp = num;
while (temp != null) {
length++;
temp = temp.next;
}
return length;
}
private static NumNode calc(NumNode a, NumNode b, int aLength, int bLength) {
NumNode aNode = a;
NumNode bNode = b;
NumNode result = new NumNode();
NumNode resultNode = result;
// 計算b連結串列再a中的起始索引
int aStartIndex = aLength - bLength;
for (int i = 0; i < aLength; i++) {
if (i >= aStartIndex) {
resultNode.num = aNode.num + bNode.num;
bNode = bNode.next;
} else
resultNode.num = aNode.num;
aNode = aNode.next;
if (aNode != null) {
resultNode.next = new NumNode();
resultNode = resultNode.next;
}
}
return result;
}
public static NumNode addition(NumNode a, NumNode b) {
NumNode result = null;
// 計算位數
int aLength = length(a);
int bLength = length(b);
if (aLength > bLength) {
result = calc(a, b, aLength, bLength);
} else {
result = calc(b, a, bLength, aLength);
}
boolean isGreater9 = true;
while (isGreater9) {
isGreater9 = false;
NumNode node = result;
while (node != null) {
// 檢查是否有大於9的節點
if (node.num > 9) {
isGreater9 = true;
break;
}
node = node.next;
}
// 沒有大於9且需要進位的節點
if (!isGreater9)
break;
node = result;
if (node.num > 9) {
// 頭節點的內容跟大於9,需要進位
result = new NumNode(1, node);
node.num = node.num - 10;
}
while (node.next != null) {
if (node.next.num > 9) {
node.num += 1;
node.next.num = node.next.num - 10;
}
node = node.next;
}
}
return result;
}
private static void print(NumNode num) {
NumNode node = num;
while (node != null) {
System.out.print(node.num);
node = node.next;
}
}
public static void main(String[] args) {
NumNode a = new NumNode(9);
a.next = new NumNode(9, new NumNode(9));
NumNode b = new NumNode(9);
// b.next = new NumNode(9, new NumNode(9));
NumNode result = addition(a, b);
print(result);
}
}
題目三

這個我寫的第一個版本,只契合類那個舉例,然後瞬間就被我推翻類,最後坐下思考類10分鐘,把這個按照二維陣列的思路解析了。
先找到最高處,然後就以最高處為一個維度,做迴圈計算出水量,還是上程式碼吧:
public class Water {
public static int waterNum(int[] steps) {
int waterNum = 0;
int max = steps[0];
for (int i = 1; i < steps.length; i++) {
if (max < steps[i])
max = steps[i];
}
for (int i = 0; i < max; i++) {
int num = 0, index = 0;
for (int n = 0; n < steps.length; n++) {
if (steps[n] - i > 0) {
if (num > 0) {
waterNum += n - index - 1;
}
num = steps[n] - i;
index = n;
}
}
}
return waterNum;
}
public static void main(String[] args) {
int[] steps = new int[] { 0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 3, 0, 1 };
int water = waterNum(steps);
System.out.println(water);
}
}
總結:
其實這幾題本身的知識點並不難,都是平時用到的,就看怎麼轉化為程式碼罷了。
第一題考察的直角座標系上怎麼計算邊長,然後根據均分等長從第一條邊挨著走,計算對應的座標,該知識點在初中就已學過。
第二題則是考察每位上的正整數加法到底最大能到多少,只要明白了這一點,把每一位上相加後,再統一做進位處理就可以了。
第三題的程式碼量是最少的,我的解題思路是二位陣列的方式, 也不算難。
近段時間正值找工作的最佳時間,本人將一些各大廠商的面試題和今年(2020)最新資料的收集,以下是部分資料截圖(所有資料均已整合成檔案,pdf壓縮打包處理)。
如有有需要的朋友可以點選這裡來獲取資料,暗號:qf