眼見不一定為實!電阻、電容和電感的實際等效模型
訊號完整性在高速電路中有著至關重要的作用,而很多訊號完整性問題需要用「阻抗」的概念來解釋和描述。
在高頻訊號下,很多器件失去了原有的特性,如我們經常聽到的「高頻時電阻不再是電阻,電容不再是電容」,這是咋回事呢?那就看今天的文章吧!
容抗的概念
電容有兩個重要特性,一個是隔直通交,另一個是電容電壓不能突變,先來看一下百度百科對容抗的解釋。

簡單說,雖然交流電能通過電容,但是不同頻率的交流電和不同容值的電容,通過時的阻礙是不一樣的,把這種阻礙稱之為容抗。
容抗與電容和頻率的大小成反比,也就是說,在相同頻率下,電容越大,容抗越小;在相同電容下,頻率越高,容抗越小。
如何理解容抗與電容大小和頻率成反比呢?
以RC一階低通濾波器舉例。
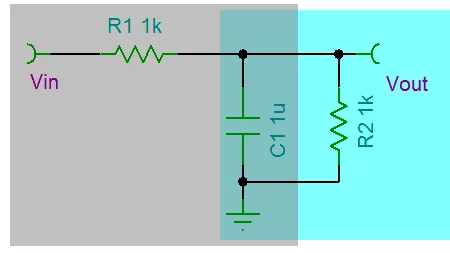
Vin通過R1電阻對電容C1進行充電,Vin的電勢加在電容C的兩個金屬極板上,正負電荷在電勢差作用下分別向電容的兩個極板聚集而形成電場,這稱為充電過程。
若將Vin拿掉,在Vout上加一個負載R2(青色部分),電容兩端的電荷會在電勢差下向負載流走,這稱為放電過程。(流過電容的電流並不是真正穿過了極板的絕緣媒介,指的是外部的電流)
衡量電容充電的電荷數是Q,Q=CV,C是常數,所以電荷數和電壓呈正比。
C=Q/V,電容量代表了電容儲存電荷的能力,微分表示式為:
C = d q ( t ) d v ( t ) (1) C=\frac{dq(t)}{dv(t)}\tag{1} C=dv(t)dq(t)(1)
電流是單位時間內電荷數的變化量: i ( t ) = d q ( t ) d t (2) i(t)=\frac{dq(t)}{dt}\tag{2} i(t)=dtdq(t)(2)
結合(1)和(2)兩個公式可得到: i ( t ) = C d v ( t ) d t (3) i(t)=C\frac{dv(t)}{dt}\tag{3} i(t)=Cdtdv(t)(3)
從公式可以看出:電容上的電流和電壓的變化量是呈正比的,或者說電容上電壓的變化量和電流是呈正比的。
即在電壓一定時,電容越大,單位時間內電路中充、放電移動的電荷量越大,電流越大,所以電容對交變電流的阻礙作用越小,即容抗越小。
在交變電流的電壓一定時,交變電流的頻率越高,電路中充、放電越頻繁,單位時間內電荷移動速率越大,電流越大,電容對交變電流的阻礙作用越小,即容抗越小。
容抗用 X C X_{C} XC表示,公式如下,其中 f f f是頻率, C C C是容值
X C = 1 ω C X_{C}=\frac1{\omega C} XC=ωC1
因為( ω = 2 π f \omega=2\pi f ω=2πf),所以容抗也可以用如下的公式表示:
X C = 1 2 π f C X_{C}=\frac1{2\pi fC} XC=2πfC1
感抗的概念
如下是百度百度對感抗的解釋,電感的特性是隔交通直,與電容是相反的;所以說容抗和感抗的性質和效果幾乎正好相反,而電阻則處在這兩個極端中間。

感抗與電感的大小和頻率成正比,也就是說,在同頻率下,電感越大,感抗越大;在同電感下,頻率越大,感抗越大。
感抗用 X L X_{L} XL表示,公式如下,其中 f f f是訊號頻率, L L L是感值
X L = ω L X_{L}=\omega L XL=ωL
因為( ω = 2 π f \omega=2\pi f ω=2πf),所以感抗的公式可以用如下表示:
X L = 2 π f L X_{L}=2\pi fL XL=2πfL
感抗和容抗又被稱為電抗,電路的總的阻抗Z由電阻R和電抗X組成。
掌握了預備知識,我們再來看電阻、電容和電感的實際等效模型。
理想的電阻、電容和電感就是如下的這樣子,在實際中並不存在,在電阻裡面會有寄生電容和寄生電感的存在,在電容裡面會有寄生電阻和寄生電感的存在,在電感裡面有寄生電阻和寄生電容。
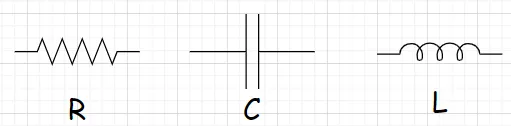
理想電阻
理想電阻的阻抗即為阻值R: Z i d e a l = R Z_{ideal}=R Zideal=R
電阻實際等效模型
電阻上會存在寄生並聯電容C寄生串聯電感L的存在。
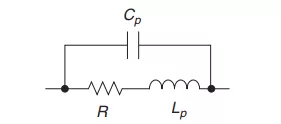
根據上圖可得電阻的實際等效阻抗為:
Z
r
e
a
l
=
(
j
ω
L
+
R
)
∗
1
j
ω
C
(
j
ω
L
+
R
)
+
1
j
ω
C
Z_{real}=\frac{(j\omega L+R)*\frac1{j\omega C}}{(j\omega L+R)+\frac1{j\omega C}}
Zreal=(jωL+R)+jωC1(jωL+R)∗jωC1
化簡可得: Z r e a l = j ω L + R ( 1 − ω 2 L C ) + j ω R C Z_{real}=\frac{j\omega L+R}{(1-\omega^2LC)+j\omega RC} Zreal=(1−ω2LC)+jωRCjωL+R
實際電阻器的阻抗和頻率曲線,有兩個節點,分別為 f 1 = 1 2 π R C f1=\frac1{2\pi RC} f1=2πRC1 f 2 = 1 2 π L C f2=\frac1{2\pi \sqrt{LC}} f2=2πLC1
在頻率小於 f 1 f1 f1時,呈現電阻特性,在 f 1 f1 f1和 f 2 f2 f2之間,呈現電容減少阻抗,頻率大於 f 2 f2 f2時,呈現電感增加阻抗的特性。
f 1 f1 f1和 f 2 f2 f2分別對應RC濾波器的截止頻率點和容抗和感抗相等時的頻率點。
![[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片儲存下來直接上傳(img-w1N4wqUL-1600407631465)(https://imgkr2.cn-bj.ufileos.com/95b8ab33-f1c3-4107-a734-7f4de50e352e.png?UCloudPublicKey=TOKEN_8d8b72be-579a-4e83-bfd0-5f6ce1546f13&Signature=ZIeYYBRfkkDfv%252BWTrfHCp81XXaQ%253D&Expires=1600423795)]](https://s3.ap-northeast-1.wasabisys.com/img.tw511.com/202009/2020092020372637u23gi2orzj3.png)
理想電容器
理想電容器的阻抗Z公式為: Z i d e a l = 1 j ω c = 1 j 2 π f c Z_{ideal}=\frac1{j\omega c}=\frac1{j2\pi fc} Zideal=jωc1=j2πfc1
阻抗大小|Z|如下圖所示,與頻率呈反比,隨著頻率增大,阻抗減小,由於理想電容器中無失真耗,故等效串聯電阻(ESR)為零。
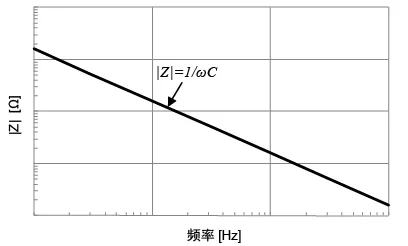
電容實際等效模型
理想的電容器在實際中是不存在的,電容的實際模型是一個ESR串聯一個ESL,再串聯一個電容,ESR是等效串聯電阻,ESL是等效串聯電感,C是理想的電容。
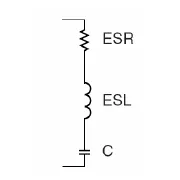
所以上述模型的復阻抗為:
Z
=
E
S
R
+
j
2
π
f
E
S
L
+
1
j
2
π
f
c
=
E
S
R
+
j
(
2
π
f
E
S
L
−
1
2
π
f
c
)
Z=ESR+j2\pi fESL+\frac1{j2\pi fc}=ESR+j(2\pi fESL-\frac1{2\pi fc})
Z=ESR+j2πfESL+j2πfc1=ESR+j(2πfESL−2πfc1)
-
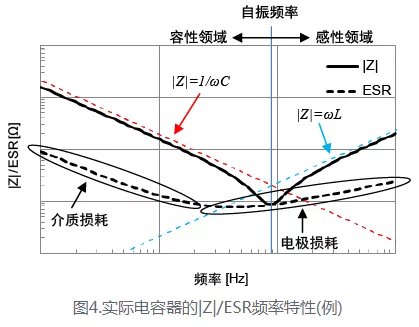
2 π f E S L < < 1 2 π f c 2\pi fESL<<\frac1{2\pi fc} 2πfESL<<2πfc1時,電容器表現為容性;
-
2 π f E S L > > 1 2 π f c 2\pi fESL>>\frac1{2\pi fc} 2πfESL>>2πfc1時,電容器表現為感性,因此會有一句話叫高頻時電容不再是電容,而呈現為電感,這個電感不是說電容變成了電感,而是指此時的電容擁有了與電感類似的特性。
-
2 π f E S L = 1 2 π f c 2\pi fESL=\frac1{2\pi fc} 2πfESL=2πfc1時,此時容抗向量等於感抗向量,電容的總阻抗最小,表現為純電阻特性,此時的f稱為電容的自諧振頻率。
自諧振頻率點是區分電容是容性還是感性的分界點,高於諧振點時,「電容不再是電容」,因此退耦作用將下降。實際電容器都有一定的工作頻率範圍,在工作頻率範圍內,電容才具有很好的退耦作用。 E S L ESL ESL是電容在高於自諧振頻率點之後退耦功能被消弱的根本原因。
下圖是實際電容器的頻率特性。
理想電感
理想電感的阻抗為: Z i d e a l = j ω L Z_{ideal}=j\omega L Zideal=jωL
電感實際等效模型
![[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片儲存下來直接上傳(img-jwL5vwB5-1600407631473)(https://imgkr2.cn-bj.ufileos.com/2a2a9340-2dd8-42d2-90d5-57369309170f.png?UCloudPublicKey=TOKEN_8d8b72be-579a-4e83-bfd0-5f6ce1546f13&Signature=hyTOx2occOgGN7c4J6Ha80nPbz8%253D&Expires=1600417943)]](https://s3.ap-northeast-1.wasabisys.com/img.tw511.com/202009/20200920203807700ffu5t3vtyzw.png)
和電阻的是一樣的,即:
Z
r
e
a
l
=
j
ω
L
+
R
(
1
−
ω
2
L
C
)
+
j
ω
R
C
Z_{real}=\frac{j\omega L+R}{(1-\omega^2LC)+j\omega RC}
Zreal=(1−ω2LC)+jωRCjωL+R
從下圖可以看出,理想的電感的阻抗是隨著頻率的增加而變大的。
等效電感的阻抗呈一個倒V型,正好和電容相反,倒V的最高點稱為電感的自諧振點。
當系統阻尼R提供的衰減不足時,容抗和感抗相互抵消,能量在LC間來回傳遞,這就是諧振。
-
頻率低於自諧振頻率SRF時,電感感抗隨著頻率增加而增加。
-
頻率等於自諧振頻率SRF時,電感感抗達到最大。
-
頻率高於自諧振頻率SRF時,電感感抗隨著頻率增加而減少。
![[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片儲存下來直接上傳(img-gzpbc9Lv-1600407631474)(https://imgkr2.cn-bj.ufileos.com/5ab7ce6d-a598-4390-b2d1-2f2b4cd7c78d.png?UCloudPublicKey=TOKEN_8d8b72be-579a-4e83-bfd0-5f6ce1546f13&Signature=xBYa3%252BMfdRMhcTxhylQlNM2sofU%253D&Expires=1600423888)]](https://s3.ap-northeast-1.wasabisys.com/img.tw511.com/202009/20200920203819111flodkb0tiie.png)
總結
理想的電阻、電容和電感在實際中不存在,都會存在寄生引數,從而在不同的頻率下,表現出的特性不同,只有在特定的頻率範圍內才能發揮出其本身的特性。
今天的文章內容到這裡就結束了,希望對你有幫助,我們下一期見。


