PID微分器與濾波器的愛恨情仇
1 先說噪聲
在電子裝置等電路系統中,噪聲是不被系統需要的電訊號;電子裝置產生的噪聲會由於多種不同的影響而產生很大的差異。
在通訊系統中,噪聲是一個錯誤或不希望出現的隨機干擾從而作用於有效的訊號。
2 噪聲對於系統的影響
噪聲出現的第一個場景,當我們在教室裡做英語聽力,然後旁邊的同學手機忽然來了一條簡訊,這時候往往可以聽到放英語聽力的喇叭會被幹擾,然後會發出嗶嗶嗶的聲音;
下面是一個正弦訊號跌加噪聲的例子,在原始訊號上疊加一定幅度的高斯噪聲,可以看到訊號不再像原來的正弦訊號那樣完美,具體如下圖所示;
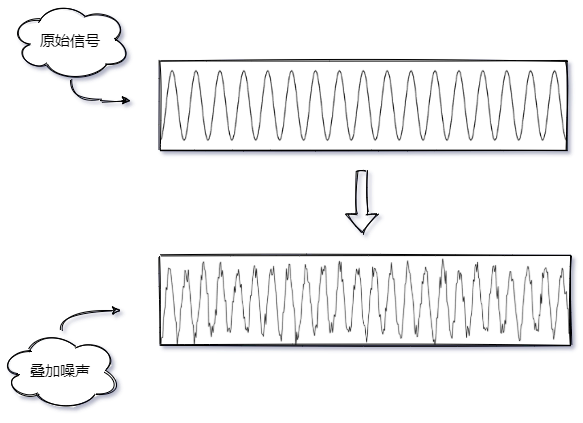
或者,很久很久以前,數位電視還沒有普及,那時候的映象管的黑白電視,也容易出現這樣的雪花一樣的噪聲,疊加在圖片上就會出現這樣的效果,具體如下圖所示;

從上述的例子中可以看到,噪聲往往會對系統造成一定程度的影響,但是如果噪聲的幅度減小到一定程度,對於系統的影響可能就沒有那麼容易被發現。
下面做一個實驗;
在一張黑色圖片上疊加幅度很小幅度的高斯噪聲;從第二張圖片中發現噪聲沒有影響到整體圖片;
然後我嘗試提高了整幅圖片的亮度,發現,噪點便開始出來了,這像極平時那些槍版影片的馬賽克畫質;
整體的實驗結果如下圖所示;

3 對於PID控制器的影響
既然噪聲的幅度減小到一定程度,對於系統的影響可能就沒有那麼容易被發現,那麼對理想的PID控制器又有什麼影響呢?
不要忘了,在理想PID控制器中,微分控制器會對偏差的變化率(斜率)進行累加,從而產生積分器的輸出;
對於微分器來說,即使噪聲幅度足夠小,但是隻要達到足夠高頻率,偏差的變化率一樣可以變得很大,下面舉個例子;
這裡有一個固定頻率
f
f
f和賦值
A
A
A的噪聲為訊號1,這個訊號可以表示為:
X
1
(
t
)
=
A
s
i
n
(
2
π
f
t
)
X_1(t) = Asin(2\pi f t)
X1(t)=Asin(2πft)
於是我們嘗試將訊號1的幅度減半,頻率變為原來的兩倍,得到了訊號2:
X
2
(
t
)
=
A
2
s
i
n
(
2
π
2
f
t
)
X_2(t) = \cfrac{A}{2} sin(2\pi 2f t)
X2(t)=2Asin(2π2ft)
以此類推,在訊號2的基礎上,幅度再減半,頻率乘以2,得到訊號3:
X
3
(
t
)
=
A
4
s
i
n
(
2
π
4
f
t
)
X_3(t) = \cfrac{A}{4} sin(2\pi 4f t)
X3(t)=4Asin(2π4ft)
簡單畫了一下這個訊號,具體如下圖所示;
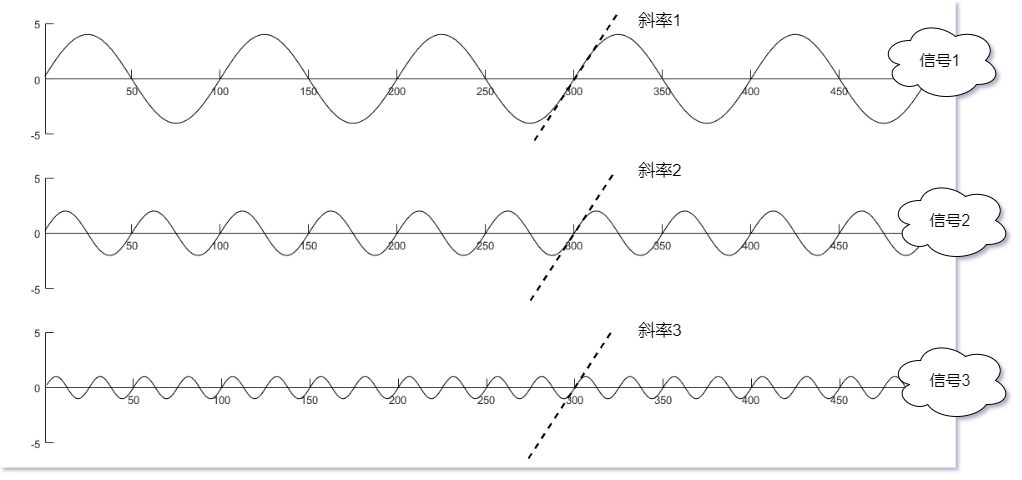
假設分別取三個訊號位於 t 0 t_0 t0該點的斜率,從圖中可以看到,斜率1,斜率2,斜率3是相同的,簡單驗證一下,在 t 0 t_0 t0時刻,可以得到:
{
D
1
=
d
X
1
(
t
)
d
t
D
2
=
d
X
2
(
t
)
d
t
D
3
=
d
X
3
(
t
)
d
t
\begin{cases}D_1 = \cfrac{dX_1(t)}{dt} \\ \\ D_2 = \cfrac{dX_2(t)}{dt} \\ \\ D_3 = \cfrac{dX_3(t)}{dt} \\ \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧D1=dtdX1(t)D2=dtdX2(t)D3=dtdX3(t)
所以這裡就是求複合函數的微分,由於選取的點比較特殊,發現最終計算得到的結果
D
1
=
D
2
=
D
3
D_1 = D_2 = D_3
D1=D2=D3,因此也可以發現,即使減小了噪聲的幅度,但是對於較高頻率的噪聲,依然會產生較大斜率。
遇到高頻噪聲,那麼微分器會產生較大的輸出,從而最終對系統造成影響,這是我們不希望出現的結果,因此在反饋迴路中並不希望高頻噪聲進入PID控制器的計算,這裡就需要低通濾波器將噪聲濾除。
4 加入濾波器
低通濾波器可以濾除高頻訊號,這樣保留了有效訊號,可以設定所需的截止頻率;
系統處理有效訊號,由於低頻部分訊雜比較高,因此噪聲對於系統的影響較小,而高頻部分,訊雜比就很低,這時候對於系統來說,噪聲就會造成不小的影響,具體如下圖所示;
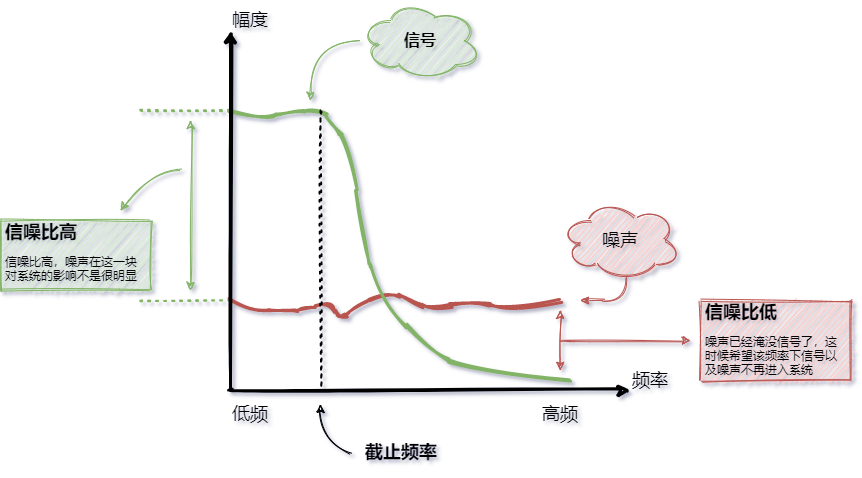
訊雜比:有效訊號和噪聲的比值,英文名稱叫做SNR或S/N(SIGNAL-NOISE RATIO);
所以下面我們會在PID控制器的微分部分加入低通濾波器,這樣對反饋的訊號進行一部分處理,從而減小系統干擾,如下圖所示;

4.1 傳遞函數
概念:拉普拉斯變換是對於 t > = 0 t>=0 t>=0 函數值不為零的連續時間函數 x ( t ) x(t) x(t) 通過關係式 (式中 − s t -st −st為自然對數底 e e e的指數)變換為復變數 s s s的函數 X ( s ) X(s) X(s)。它也是時間函數 x ( t ) x(t) x(t)的「複頻域」表示方式。
也就是說拉式變換可以將時域關係變換到頻域中,這樣可以便於系統進行分析。
下面是本文下面會用到的時域函數對應的拉普拉斯變換:
- 積分: 1 s \cfrac{1}{s} s1
- 微分: s s s
- 低通濾波器的傳遞函數: N s + N \cfrac{N}{s+N} s+NN
低通濾波器中的截止頻率即為 N N N,單位是 r a d / s rad/s rad/s;
4.2 串聯微分的等效形式反饋積分
串聯等效傳遞函數的關係為,兩個方框串聯等於各個方框傳遞函數的乘積;
具體如下所示;
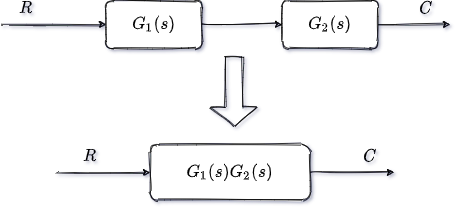
因此低通濾波串聯微分的傳遞函數為:
s
N
s
+
N
\cfrac{sN}{s+N}
s+NsN
閉環負反饋的等效傳遞函數的關係如下所示;

這裡我們可以使用負反饋積分的方式,構建等效於串聯微分的傳遞函數,最終的傳遞函數結果是相同的,具體如下圖所示;

串聯微分的形式,可能在演演算法的實現上會更加直觀,但是會比較費資源;
使用負反饋積分的等效形式進行實現,則進一步減少了演演算法的資源消耗,下面給出一個TI公司的PID演演算法實現就是通過負反饋積分的等效形式進行實現的。
5 C語言實現
這裡直接使用了TI公司的PID演演算法,對於微分部分做了濾波的處理,並且使用的是負反饋積分的方式,
具體可以參考controlSUITE\libs\app_libs\motor_control\math_blocks\v4.2\pid_grando.h
PID控制器的整體框圖如下所示,我們只關心微分部分;

首先可以發現
u
d
u_d
ud滿足:
u
d
(
k
)
=
K
d
[
c
2
u
i
(
k
−
1
)
+
c
1
e
(
k
)
−
c
1
e
(
k
−
1
)
]
u_d(k) = K_d\Big[c_2u_i(k-1)+c_1e(k)-c_1e(k-1) \Big]
ud(k)=Kd[c2ui(k−1)+c1e(k)−c1e(k−1)]
這裡濾波器有兩個係數
c
1
c_1
c1和
c
2
c_2
c2,它們必須滿足截止頻率
a
a
a(單位Hz)和取樣週期
T
T
T(單位秒)以下的關係:
{
c
1
=
a
c
2
=
1
−
c
1
T
\begin{cases}c_1 = a\\ c_2 = 1-c_1T \end{cases}
{c1=ac2=1−c1T
C語言實現如下:
/* =================================================================================
File name: PID_GRANDO.H
===================================================================================*/
#ifndef __PID_H__
#define __PID_H__
typedef struct { _iq Ref; // Input: reference set-point
_iq Fbk; // Input: feedback
_iq Out; // Output: controller output
_iq c1; // Internal: derivative filter coefficient 1
_iq c2; // Internal: derivative filter coefficient 2
} PID_TERMINALS;
// note: c1 & c2 placed here to keep structure size under 8 words
typedef struct { _iq Kr; // Parameter: reference set-point weighting
_iq Kp; // Parameter: proportional loop gain
_iq Ki; // Parameter: integral gain
_iq Kd; // Parameter: derivative gain
_iq Km; // Parameter: derivative weighting
_iq Umax; // Parameter: upper saturation limit
_iq Umin; // Parameter: lower saturation limit
} PID_PARAMETERS;
typedef struct { _iq up; // Data: proportional term
_iq ui; // Data: integral term
_iq ud; // Data: derivative term
_iq v1; // Data: pre-saturated controller output
_iq i1; // Data: integrator storage: ui(k-1)
_iq d1; // Data: differentiator storage: ud(k-1)
_iq d2; // Data: differentiator storage: d2(k-1)
_iq w1; // Data: saturation record: [u(k-1) - v(k-1)]
} PID_DATA;
typedef struct { PID_TERMINALS term;
PID_PARAMETERS param;
PID_DATA data;
} PID_CONTROLLER;
/*-----------------------------------------------------------------------------
Default initalisation values for the PID objects
-----------------------------------------------------------------------------*/
#define PID_TERM_DEFAULTS { \
0, \
0, \
0, \
0, \
0 \
}
#define PID_PARAM_DEFAULTS { \
_IQ(1.0), \
_IQ(1.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(1.0), \
_IQ(1.0), \
_IQ(-1.0) \
}
#define PID_DATA_DEFAULTS { \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(1.0) \
}
/*------------------------------------------------------------------------------
PID Macro Definition
------------------------------------------------------------------------------*/
#define PID_MACRO(v) \
\
/* proportional term */ \
v.data.up = _IQmpy(v.param.Kr, v.term.Ref) - v.term.Fbk; \
\
/* integral term */ \
v.data.ui = _IQmpy(v.param.Ki, _IQmpy(v.data.w1, \
(v.term.Ref - v.term.Fbk))) + v.data.i1; \
v.data.i1 = v.data.ui; \
\
/* derivative term */ \
v.data.d2 = _IQmpy(v.param.Kd, _IQmpy(v.term.c1, \
(_IQmpy(v.term.Ref, v.param.Km) - v.term.Fbk))) - v.data.d2;\
v.data.ud = v.data.d2 + v.data.d1; \
v.data.d1 = _IQmpy(v.data.ud, v.term.c2); \
\
/* control output */ \
v.data.v1 = _IQmpy(v.param.Kp, \
(v.data.up + v.data.ui + v.data.ud)); \
v.term.Out= _IQsat(v.data.v1, v.param.Umax, v.param.Umin); \
v.data.w1 = (v.term.Out == v.data.v1) ? _IQ(1.0) : _IQ(0.0);\
#endif // __PID_H__
6 參考
https://en.wikipedia.org/wiki/Low-pass_filter
自動控制原理 第五版 胡壽鬆 P47
雖然寫的不一定是最好,但是每一個字、每一個公式都是用心碼的,每一張圖都是用心畫的,每一句話都是加入了自己的理解,如果幫到了你,請無情三連吧;另外筆者能力有限,文中難免存在錯誤和紕漏,望輕拍指正。

