2020CCPC網路賽1005 Lunch （變形Nim博弈）

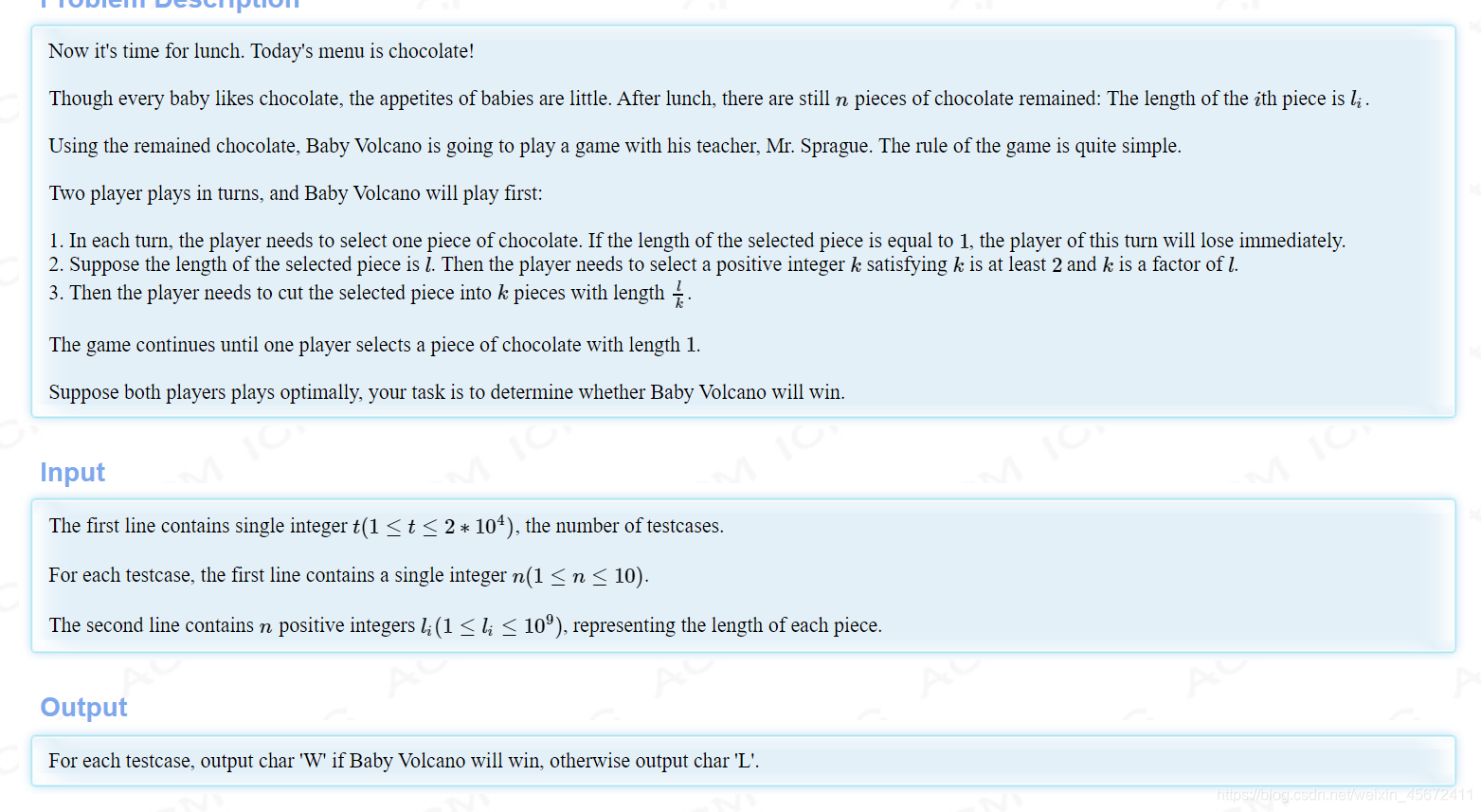
題意：給定你n個巧克力塊，每一塊巧克力的長度為l[i],兩個人輪流操作，每一次操作選擇一個當前的長度l的一個大於等於2的因子，然後將這個巧克力分為l/factor(l)塊，當所有的巧克力變為1之後，此時再進行操作的人就會輸掉遊戲，問你當前給定n和每個巧克力的l[i]後，先手是輸還是贏。

思路：當看到先手是贏還輸的情況後，就可以想到應該是個博弈問題。然後我們可以想到假如一個長度被分成了偶數個巧克力塊，增加的操作次數為偶數，那麼他並不會改變當前狀態下的勝負關係。而假如是增加的奇數次數的巧克力塊的話，當前狀態下的勝負關係是會發生改變的。
並且因為上面我們說的增加偶數個是對勝負關係沒有貢獻的，因此假如這個數因數中有多個2的話，我們只需要就算一個，因為再多的2和一個2的貢獻是一樣的，然後計算它的質因數的個數，也就是質因數分解下的每個質因子的冪次數相加。
這樣就相當於與把一塊巧克力用它含有的質因數個數代替了，因為這些質因數都是互不影響的個體，可以類似把他們看做一推石子中的每一個石子，因此這個問題就變成了Nim遊戲的形式了，把他們的質因數的個數互斥或和求出即可得到答案了。

MAXN太大會超時的，5e4就夠用了。
程式碼：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define inf 0x3f3f3f3f
const int MAXN = 5e4+7;//篩素因子打到 根號N即可
int prime[MAXN],cnt;
bool vis[MAXN];
//考慮質因數分解
void Prime()//尤拉篩求一下質數
{
	for(int i = 2;i < MAXN;i ++){
		if(!vis[i])
			prime[++cnt] = i;
		for(int j = 1;j <= cnt&&prime[j]*i < MAXN;j ++){
			vis[prime[j]*i] = 1;
			if(i % prime[j] == 0)
				break;
		}
	}
}
//直接因數分解 會超時 所以先用線性篩 把素數處理一下 然後再直接用素因數篩
//因為先把合數因子去掉了 所以簡單的質因子分解 是遍歷所有根號n前面的數 但是這個題會超時 所以就先打出素因子直接處理素因子即可 
int a[17],num[17];

int main()
{
	int T,n;
	Prime();
	scanf("%d",&T);
	while(T--){
		memset(num,0,sizeof(num));
		scanf("%d",&n);
		for(int i = 1;i <= n;i ++){
			scanf("%d",&a[i]);
		}
		int cot = 0;
		int ans = 0;
		for(int i = 1;i <= n;i ++){
			if(a[i]%2 == 0) num[i]++;//因數2的貢獻只計算一次 因為他並不會改變 當前的勝負關係 所以多個和一個的作用效果是一樣的
			while(a[i]%2 == 0){
				a[i] >>= 1;
			}
			for(int j = 1;j <= cnt && prime[j] <= a[i];j ++){
				while(a[i]%prime[j] == 0){
					num[i]++;
					a[i] /= prime[j];
				}
			}
			if(a[i] > 1) num[i]++;//大於1就還要再分解一次
			ans ^= num[i];
		}
		if(ans) puts("W");
		else puts("L");
	}
	return 0;
}