Kaggle實戰入門（三）之紐約出租車價格預測New-York-City-Taxi-Fare-Prediction

今天給大家分享第三個kaggle競賽專案，紐約出租車價格預測New-York-City-Taxi-Fare-Prediction。這個專案的特點是給到我們的資料集比較大，有5.3G，資料總量是5400W行。不過我們在做這個專案的時候並不需要這麼多的資料量，下面我們就一起來看一下這個專案。

Part1.資料匯入和初步分析

首先匯入我們的資料集，由於資料量過大，我們只匯入前500W行的資料進行建模。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

train = pd.read_csv('train.csv',nrows=5000000)
test = pd.read_csv('test.csv')
test_ids = test['key']

train.head()

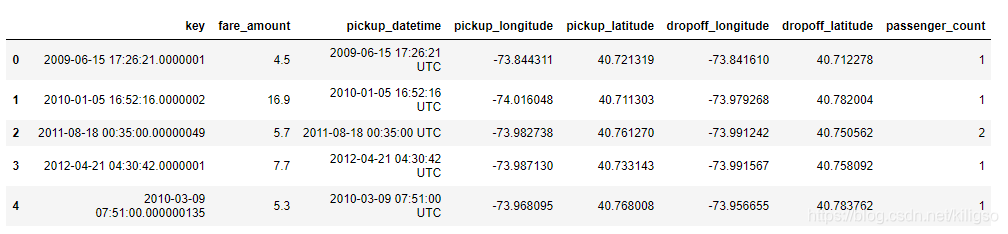
可以看到我們本次的資料特徵量還是比較少的，雖然資料總量大，特徵只有8個。

train.info()

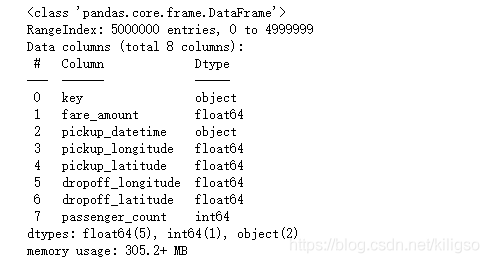
key：索引
fare_amount：價格
pickup_datetime：計程車接到客人的時間
pickup_longitude：出發時的經度
pickup_latitude：出發時的緯度
dropoff_longitude：到達時的經度
dropoff_latitude：到達時的緯度
passenger_count：乘客的數目

train.describe()

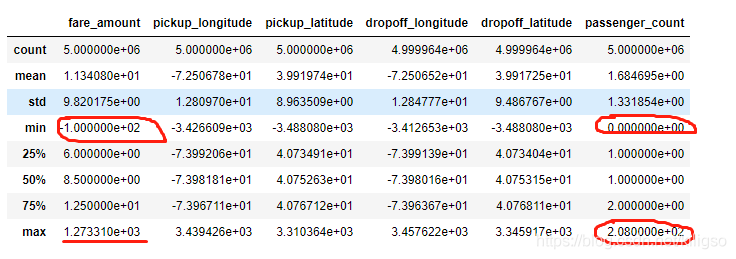
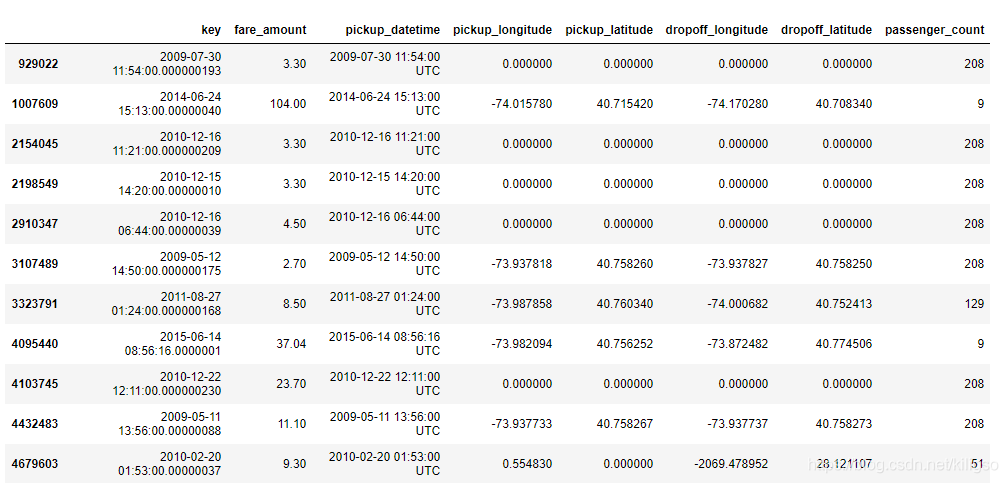
紅圈圈住的資料當中是異常值：負的價格，乘客數目最小為0，乘客數目最大為208
而橫線劃出來的資料令人疑惑：什麼樣的旅程會產生1270的出租費用呢？

Part2.資料分析

首先觀察價格特徵的分佈：

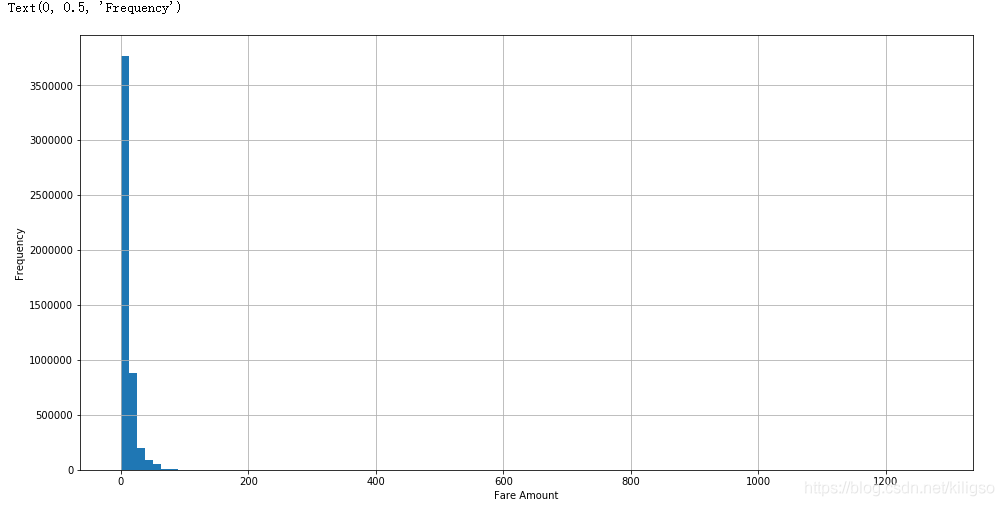
train.fare_amount.hist(bins=100,figsize = (16,8))
plt.xlabel("Fare Amount")
plt.ylabel("Frequency")

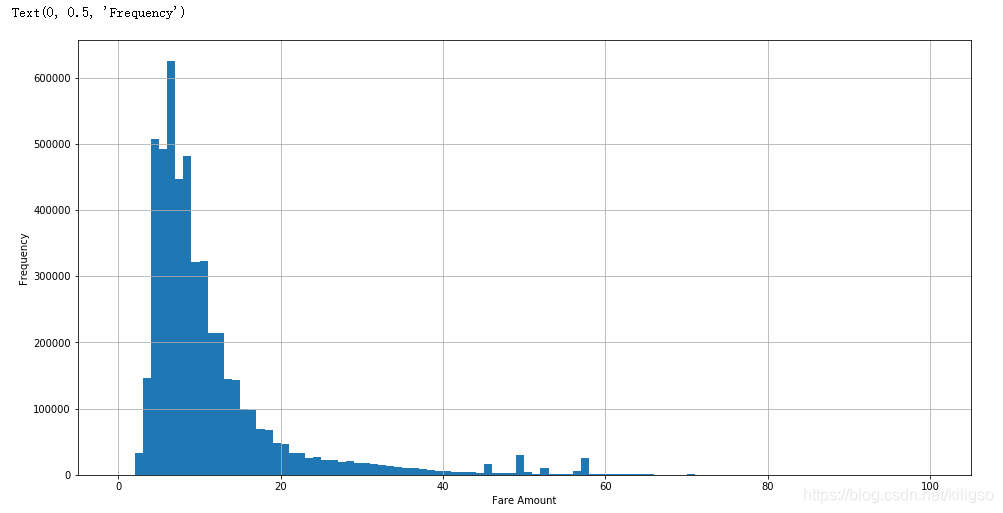
train[train.fare_amount <100 ].fare_amount.hist(bins=100, figsize = (16,8))
plt.xlabel("Fare Amount")
plt.ylabel("Frequency")

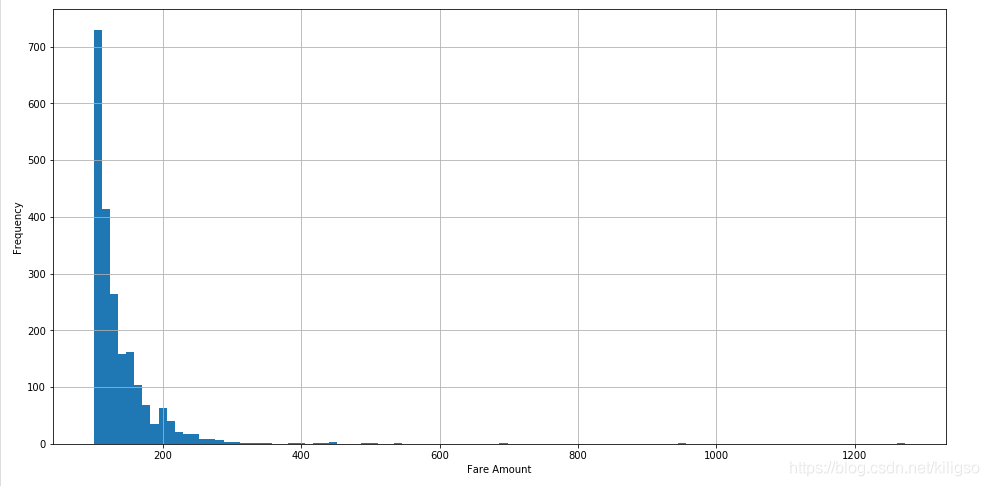
train[train.fare_amount >=100 ].fare_amount.hist(bins=100, figsize = (16,8))
plt.xlabel("Fare Amount")
plt.ylabel("Frequency")

train[train.fare_amount <100].shape

train[train.fare_amount >=100].shape

由上面的程式碼和圖我們可以得到幾個結論：
1、價格的分佈大多數是在100以內的，少部分在100以上
2、100以內的價格大多數集中在0~20之間
3、100以外的價格大多數集中在200附近，有幾個比較大的價格可能是異常值，也可能是去往機場的價格。

接下來觀察乘客數目的分佈：

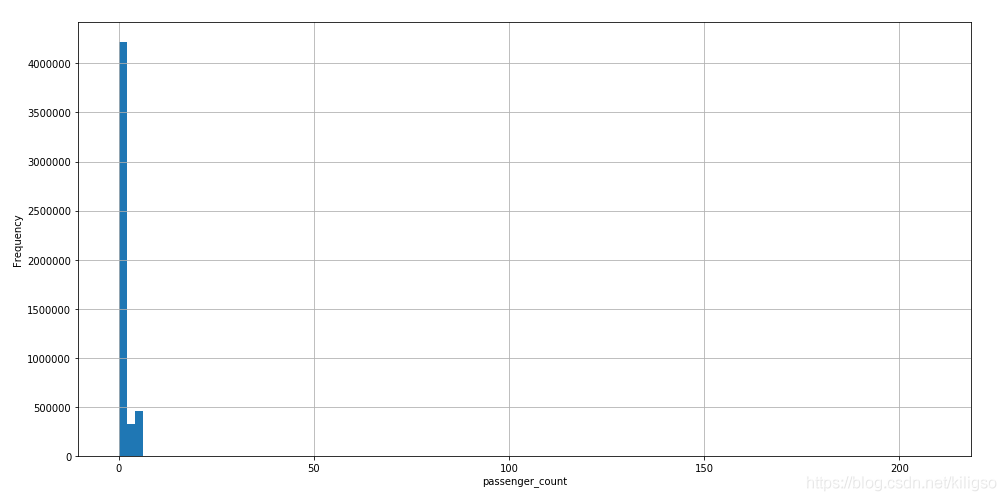
train.passenger_count.hist(bins=100,figsize = (16,8))
plt.xlabel("passenger_count")
plt.ylabel("Frequency")

train[train.passenger_count<10].passenger_count.hist(bins=10,figsize = (16,8))
plt.xlabel("passenger_count")
plt.ylabel("Frequency")

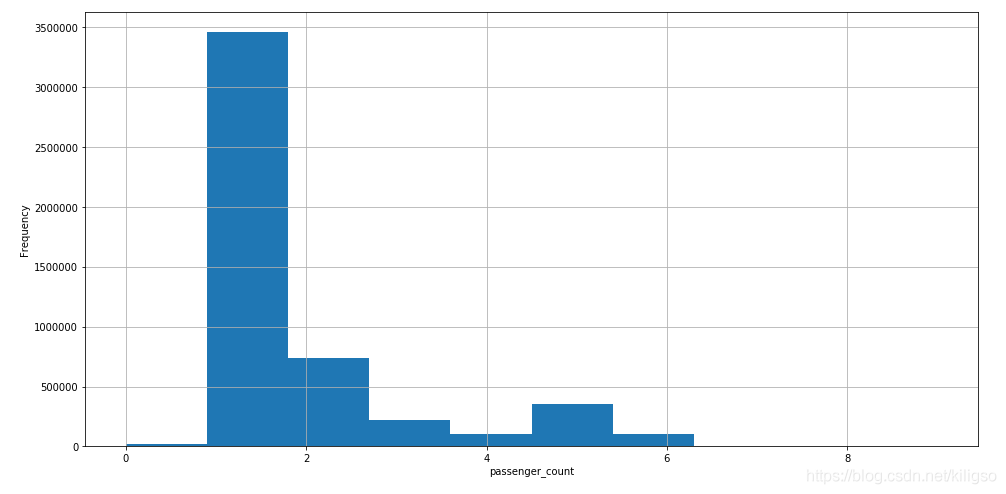
train[train.passenger_count<7].passenger_count.hist(bins=10,figsize = (16,8))
plt.xlabel("passenger_count")
plt.ylabel("Frequency")

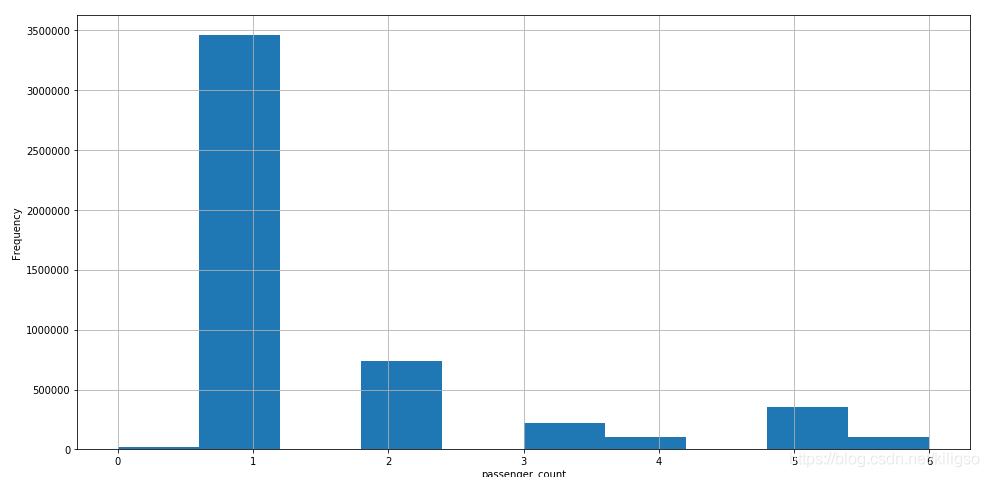
train[train.passenger_count>7].passenger_count.hist(bins=10,figsize = (16,8))
plt.xlabel("passenger_count")
plt.ylabel("Frequency")

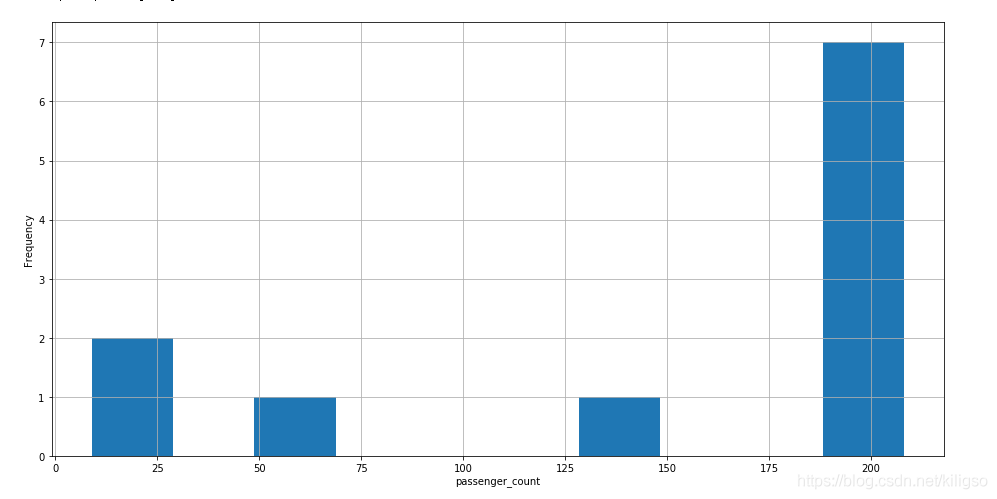
train[train.passenger_count >7]

train[train.passenger_count ==0].shape

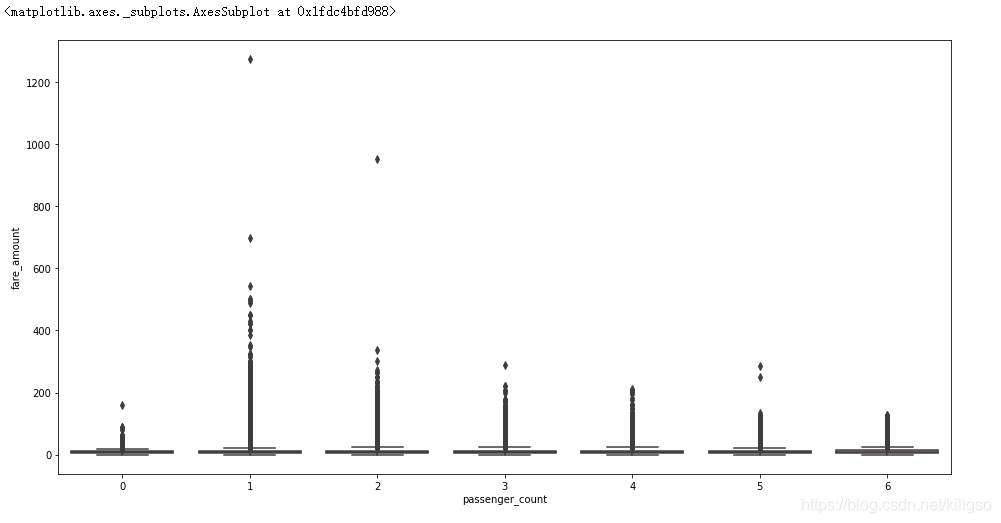
plt.figure(figsize= (16,8))
sns.boxplot(x = train[train.passenger_count< 7].passenger_count, y = train.fare_amount)

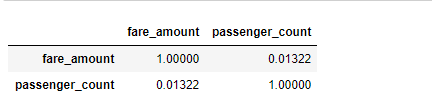
train[train.passenger_count <7][['fare_amount','passenger_count']].corr()

由上面的程式碼和圖我們可以得到幾個結論：
1、人數的分佈大多數都在7以內，少部分在7以外
2、人數為7以外的資料中大部分資料座標有缺失且人數都為208
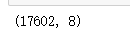
3、有17602個資料是乘客人數為0，有可能是運貨的計程車，也有可能是資料的缺失
4、由箱型圖可以看出，人數小於7的計程車平均價格都比較接近
5、使用.corr()介面檢視passenger_count 與fare_amount的關聯程度並不高只有0.013

Part3.資料處理

1、空值處理

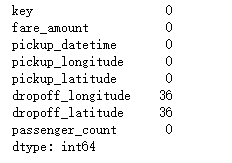
train.isnull().sum()#找出空值

train = train.dropna(how='any', axis=0)

36個缺失值對於我們500W的資料量顯得微不足道，所以我選擇直接將缺失值去掉

test = pd.read_csv('test.csv')
test_ids = test['key']
test.head()
test.isnull().sum()

對測試集進行同樣的處理，不過測試集並沒有缺失值

2、異常值處理

train = train[train.fare_amount>=0]

將價格為負數的資料去除

3、特徵工程
①縮短訓練集的範圍
由於訓練集的資料量比較大，我們可以根據測試集的座標範圍來對訓練集進行一定的縮減

print(min(test.pickup_longitude.min(),test.dropoff_longitude.min()))
print(max(test.pickup_longitude.max(),test.dropoff_longitude.max()))
print(min(test.pickup_latitude.min(),test.dropoff_latitude.min()))
print(max(test.pickup_latitude.max(),test.dropoff_latitude.max()))

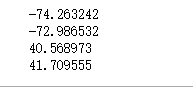
得到了-74.2到-73作為經度的選取範圍，40.5到41.8作為緯度的選取範圍

def select_train(df, fw):
    return (df.pickup_longitude >= fw[0]) & (df.pickup_longitude <= fw[1]) & \
           (df.pickup_latitude >= fw[2]) & (df.pickup_latitude <= fw[3]) & \
           (df.dropoff_longitude >= fw[0]) & (df.dropoff_longitude <= fw[1]) & \
           (df.dropoff_latitude >= fw[2]) & (df.dropoff_latitude <= fw[3])
fw = (-74.2, -73, 40.5, 41.8)
train = train[select_train(train, fw)]

利用select_train將訓練集資料進行縮減

②構造新的時間特徵
原本的時間特徵並不適合我們直接使用，考慮到計程車不同時間段，不同年份，月份都可能會提價，我們要在原本的時間特徵中提取出新的年，月，日，時作為新的特徵，供我們的模型使用。

def deal_time_features(df):
    df['pickup_datetime'] = df['pickup_datetime'].str.slice(0, 16)
    df['pickup_datetime'] = pd.to_datetime(df['pickup_datetime'], utc=True, format='%Y-%m-%d %H:%M')
    df['hour'] = df.pickup_datetime.dt.hour
    df['month'] = df.pickup_datetime.dt.month
    df["year"] = df.pickup_datetime.dt.year
    df["weekday"] = df.pickup_datetime.dt.weekday
    return df
train = deal_time_features(train)
test = deal_time_features(test)

train.head()

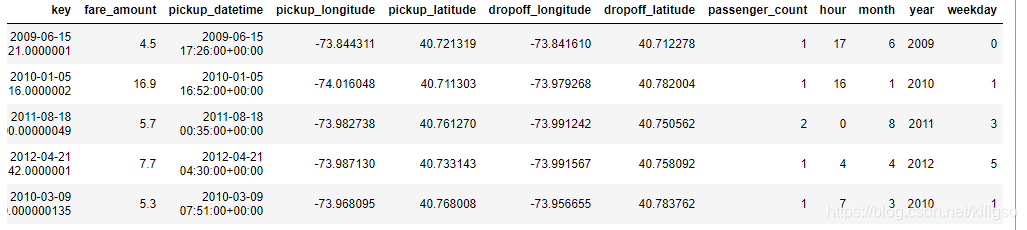
處理後的時間特徵由時，月，年，周幾組成

③構造新的距離特徵
直接使用經緯度座標不利於我們的模型運轉，我們用轉換公式將經緯度座標轉化為距離

def distance(x1, y1, x2, y2):
    p = 0.017453292519943295 
    a = 0.5 - np.cos((x2 - x1) * p)/2 + np.cos(x1 * p) * np.cos(x2 * p) * (1 - np.cos((y2 - y1) * p)) / 2
    dis = 0.6213712 * 12742 * np.arcsin(np.sqrt(a))
    return dis  
train['distance_miles'] = distance(train.pickup_latitude,train.pickup_longitude,train.dropoff_latitude,train.dropoff_longitude)
test['distance_miles'] = distance(test.pickup_latitude, test.pickup_longitude,test.dropoff_latitude,test.dropoff_longitude)
train.head()

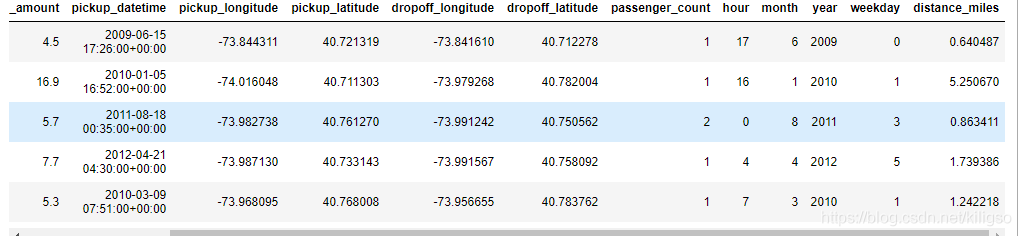
train[(train['distance_miles']==0)&(train['fare_amount']==0)]

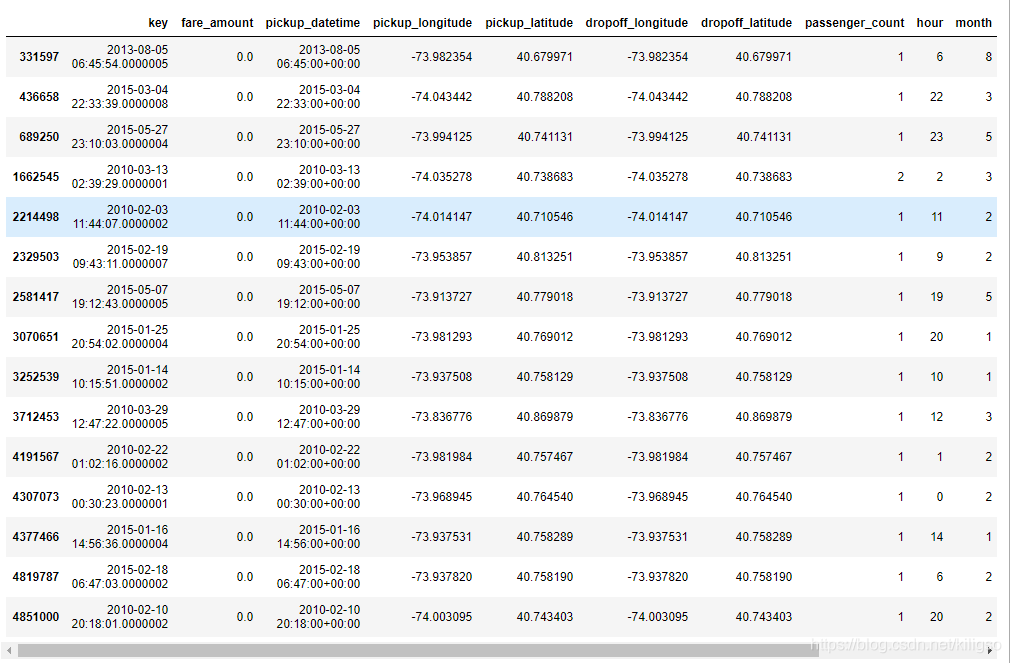
構造完距離特徵後，我們會發現還有15個距離和價格都為0的無用資料，可以將它刪除

train = train.drop(index= train[(train['distance_miles']==0)&(train['fare_amount']==0)].index, axis=0)

④特殊處理
1、刪除fare_amount小於2.5的資料，因為紐約出租車的起步價為2.5

train = train.drop(index= train[train['fare_amount'] < 2.5].index, axis=0)

2、去除人數大於7的資料

train[train.passenger_count >= 7]

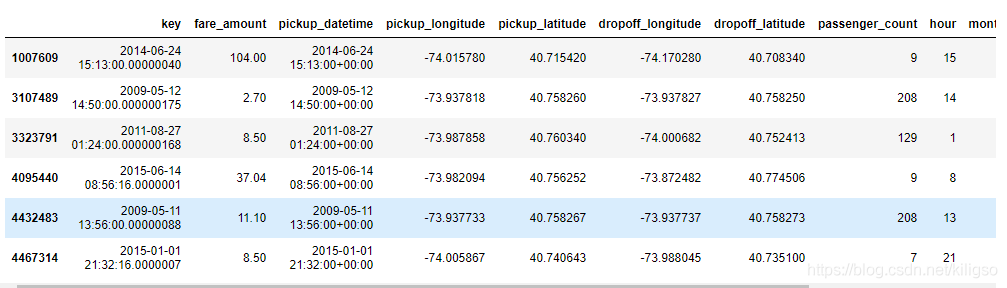
train = train.drop(index= train[train.passenger_count >= 7].index, axis=0)

Part4.資料建模

看一下資料處理完後的最終樣子

train.describe().T

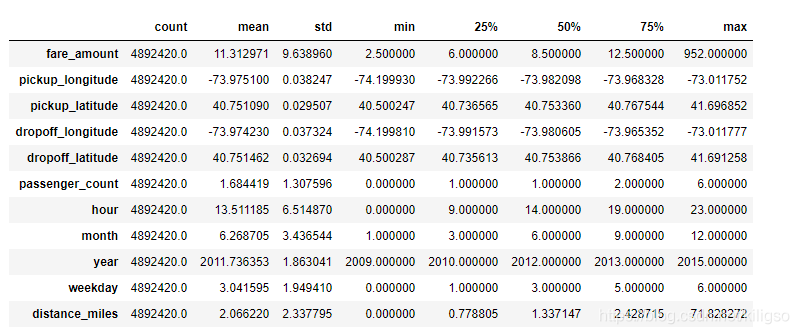
利用.corr介面看下這些新的特徵跟價格的關聯

train.corr()['fare_amount']

進入建模的步驟：

df_train = train.drop(columns= ['key','pickup_datetime'], axis= 1).copy()
df_test = test.drop(columns= ['key','pickup_datetime'], axis= 1).copy()
#使用copy後的資料進行建模


from sklearn.model_selection import train_test_split 
X_train, X_test, y_train, y_test = train_test_split(df_train.drop('fare_amount',axis=1)
                                                    ,df_train['fare_amount']
                                                    ,test_size=0.2
                                                    ,random_state = 42)


#用train_test_split分出訓練集和測試集

import xgboost as xgb
params = { 
    'max_depth': 7,
    'gamma' :0,
    'eta':0.3, 
    'subsample': 1,
    'colsample_bytree': 0.9, 
    'objective':'reg:linear',
    'eval_metric':'rmse',
    'silent': 0
}
def XGBmodel(X_train,X_test,y_train,y_test,params):
    matrix_train = xgb.DMatrix(X_train,label=y_train)
    matrix_test = xgb.DMatrix(X_test,label=y_test)
    model=xgb.train(params=params,
                    dtrain=matrix_train,
                    num_boost_round=5000, 
                    early_stopping_rounds=10,
                    evals=[(matrix_test,'test')])
    return model

model = XGBmodel(X_train,X_test,y_train,y_test,params)

#建模

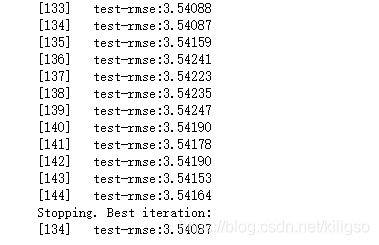
prediction = model.predict(xgb.DMatrix(df_test), ntree_limit = model.best_ntree_limit)
prediction
#資料預測

res = pd.DataFrame()
res['key'] = test_ids
res['fare_amount'] = prediction
res.to_csv('submission.csv', index=False)
#結果儲存

Part5.小結

我的做法只是比較簡單的思路，因為計程車價格我能想到的有關價格的因素只有不同時間段，還有距離，這兩個因素影響的程度會比較大。如果有其他更好的想法和做法的話，歡迎在討論區裡面留言告訴博主。
另外，在kaggle社群上有一種做法是構造一個新的特徵，代表座標到當地三個不同機場的距離，這種做法博主在未調參時直接去使用，結果提高了0.03，我覺得提高並不算太大，作用也與距離有點重合，所以我最後沒有采用。這裡也貼出來分享給大家。

# def transform(data):
#     # Distances to nearby airports, 
#     jfk = (-73.7781, 40.6413)
#     ewr = (-74.1745, 40.6895)
#     lgr = (-73.8740, 40.7769)

#     data['pickup_distance_to_jfk'] = distance(jfk[1], jfk[0],
#                                          data['pickup_latitude'], data['pickup_longitude'])
#     data['dropoff_distance_to_jfk'] = distance(jfk[1], jfk[0],
#                                            data['dropoff_latitude'], data['dropoff_longitude'])
#     data['pickup_distance_to_ewr'] = distance(ewr[1], ewr[0], 
#                                           data['pickup_latitude'], data['pickup_longitude'])
#     data['dropoff_distance_to_ewr'] = distance(ewr[1], ewr[0],
#                                            data['dropoff_latitude'], data['dropoff_longitude'])
#     data['pickup_distance_to_lgr'] = distance(lgr[1], lgr[0],
#                                           data['pickup_latitude'], data['pickup_longitude'])
#     data['dropoff_distance_to_lgr'] = distance(lgr[1], lgr[0],
#                                            data['dropoff_latitude'], data['dropoff_longitude'])
    
#     return data

# train = transform(train)
# test = transform(test)

謝謝你們的閱讀！