手動反爬蟲：原博地址

 知識梳理不易，請尊重勞動成果，文章僅釋出在CSDN網站上，在其他網站看到該博文均屬於未經作者授權的惡意爬取資訊

如若轉載，請標明出處，謝謝！

前言

前一篇部落格對決策樹模型進行了詳解，屬於建立模型的基礎，如果想要機器學習的效果更好，單靠建立的一棵樹是遠遠不夠的，因此就有單個不行，群毆走起的套路，這樣用來提升整體模型的效果，那麼也就有了整合演演算法，使用多個樹建立模型。

整合演演算法（Ensemble learning）：顧名思義就是集合了多種演演算法的結果從而使模型的預測效果表現地更好（以量取勝，基本上都是使用樹模型）

那麼涉及到多棵樹（多種演演算法），自然也就有了多種不同的使用方式，結合初中物理的電路知識，對比電阻的放置情況，就有了串聯和並聯和串並聯等。整合演演算法模型目前常用的三種分別是Bagging、Boosting、Stacking，將其和電路進行類比方便我們理解，如下表

整合演演算法模型	原理	電路模型
Bagging	訓練多個分類器取平均 $f(x)=\frac{1}{M}\sum_{m=1}^{M}f_{m}(x)$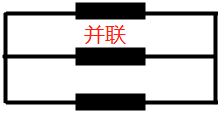
Boosting	從弱學習器開始加強，通過加權來進行訓練（加入一棵樹，要比原來強） $F_{m}(x) =F_{m-1}(x) + argmin_{h}\sum_{i=1}^{n}L(y_{i},F_{m-1}(x_{I}) +h(x_{i}) )$
Stacking	聚合多個分類或迴歸模型（可以分階段來做）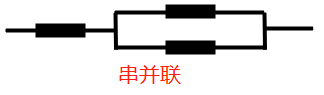

接下來就分別介紹這三種演演算法以及對應的經典的代表

一、隨機森林演演算法原理

首先是Bagging模型，其全稱為：bootstrap aggregation，說大白話就是並行（並行：就是各玩各的，互不影響）訓練了一堆分類器，其中最典型的代表就是隨機森林。

關於隨機森林的認識，單從字面上的意思進行理解即可，分為兩塊。

一個是隨機，即是資料取樣隨機，特徵選擇隨機；
一個是森林，即是把很多很多的決策樹並行放在一起；

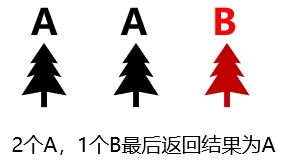
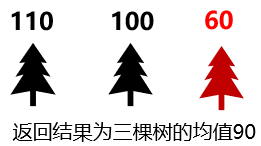
最後進行計算，如果是分類任務就是實行 眾數取值 ，如果是迴歸就是進行 平均取值 ，以三棵樹為例，對應如下

分類	迴歸

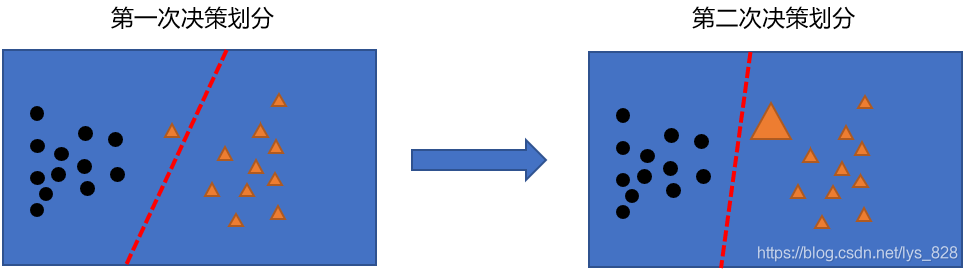
關於隨機森林的理解，首先理解一下森林，就是將多個決策樹進行組合放在一起，這個是沒有太大的問題，那麼為啥要隨機呢？不隨機會有什麼現象呢，這裡就假設用了100個樹建立模型，輸入的都是同一個資料，特徵也選擇的一樣，那麼經過訓練後自然對應每一棵樹中的節點都是相同的，最後分類或者回歸的結果都是一致的，那麼在計算最後的結果時候還是和一棵樹的結果是一樣的，也就沒有必要再進行100棵樹的組合了。

所以就有了隨機的要求，為了儘可能的保證模型的效果好，採用的是亂資料樣本和隨機特徵，這裡假設有100條資料，每次建立一棵樹都隨機取80%的資料，然後在每個資料中取60%的特徵，這樣進行訓練模型，必然最後的結果會有所不同，也就可以實現資料的分類與迴歸，圖解如下：（為了繪圖方便，這裡以建立2個樹為例），由於存在著兩重隨機性，基本上可以使得每棵樹都不會一樣，最終的結果也就會不一樣

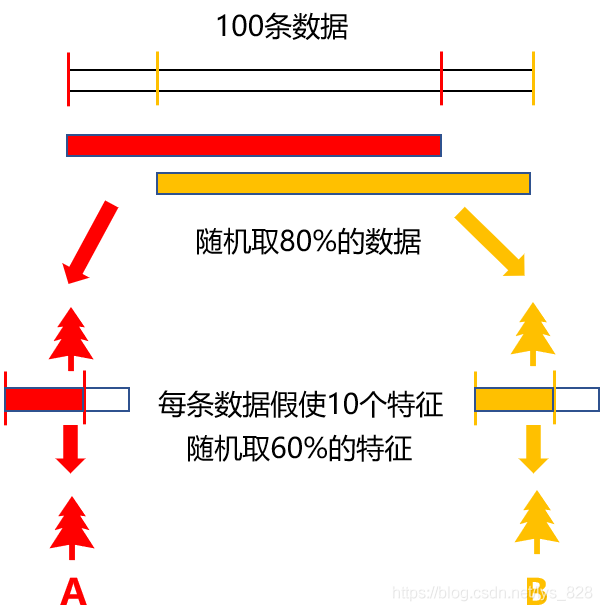
在這裡插入圖片描述
決策樹的數量問題：是不是給的樹越多，最後的模型效果越好呢？下圖是建立模型後使用不同樹的數量進行繪製的圖形

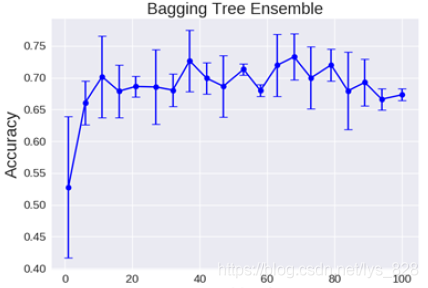
理論上越多的樹效果會越好，由上圖中可以看出，實際上基本超過一定數量就差不多上下浮動了，樹越多模型執行的時間越長，然而模型的效果也不是一定會很好，因此為了合理的選擇決策樹的數量，只能說差不多就行了。

二、隨機森林的優勢與特徵重要性指標

1.隨機森林的優勢

（1）可以進行視覺化展示，便於分析，由於採用的是樹模型，可以直接通過程式碼生成圖例展示出每一步的過程，所以其可解釋性非常非常的強（對比神經網路，雖然其效果很強大，但是類似黑盒子，無法解析）
（2）可以處理很多高緯度（feature很多）的資料，並且不用做特徵選擇
（3）在訓練完成後，能夠給出哪些feature比較重要
（4）容易做成並行化方法，速度比較快（就是每個樹之間各玩各的，互不影響）

2.特徵重要性指標

關於（1）（4）都比較容易理解，那麼關於（2）（3）的話這裡進行解析一下，首先舉個例子，一組資料中有ABCD，其中A代表age年齡特徵，模型訓練完之後就想知道A特徵有多重要。那麼怎麼評估 A的重要性？

首先是假設A中有五條資料分別為：21，23，25，37，46，51，那麼第一次建立模型執行，計算錯誤率假設為 $err_{1}$ ,要看一個特徵重要的程度，只要把這個特徵破壞掉，看對模型最後的錯誤率對造成什麼影響（就類似看一個人在團隊的重要程度，可以將其開除掉或者變換崗位之後看看對團隊的建設有什麼影響），於是就可以破壞A特徵，假使進行資料的亂序或者給定完全不相關的值，比如變成了體重的數值（111，120，89，70，170，200），此時對應的錯誤率假設為 $err_{2}$

評判重要程度就變成了 $err_{1}$ 與 $err_{2}$ 的對比，如果兩者約相等或者變化不大的話，說明這個特徵A很不重要，已經破壞了，錯誤率竟然沒有變化，證明是可有可無的地位，如果 $err_{2}$ 遠大於 $err_{1}$ ，說明特徵A的重要性極強，破話它之後導致整個模型的錯誤率顯著提高，會不會存在 $err_{2}$ 還小於 $err_{1}$ 的情況呢，理論上是可能的，但是實際上不太現實，因為是破壞了特徵A中的資料，造成的誤差只可能比原來的還大，所以這種情況可以不用考慮。

然後就是隨機森林採用的是樹模型，其中節點的選擇就是按照特徵分類的重要性來設定的，因此通過每次分裂的節點就可以知道哪些特徵比較重要，在訓練模型完成之後也可以繪製特徵重要性的條狀圖，方便視覺化展示，這裡給出的圖示，後面會有程式碼實現。
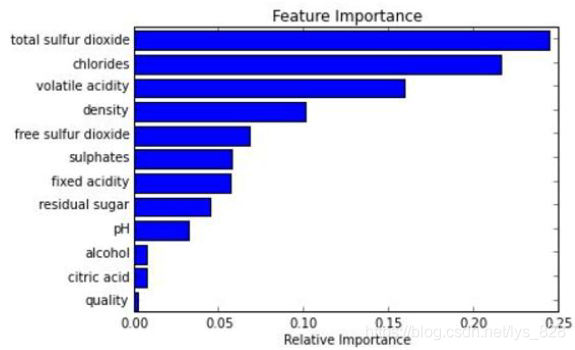
在這裡插入圖片描述

三、提升演演算法概述

還是以一個例子開始入手，假設預測使用者花費label：1000，那麼使用隨機森林模型，假定給出三棵樹，分別得到的結果為1110,900,1200，最後隨機森林預測的結果就為（1100+1200+900）/3 = 1100，對比電路模型，就是屬於並聯，取多個樹的結果然後再計算均值（這個例子是迴歸任務）

那麼使用提升演演算法Boosting該如何實現呢？，還是對比電路模型，它是首先有第一棵樹，如果不行的話再加第二棵樹，依次往後。比如首先建立第一棵樹，預測的值為950，那麼建立的第二棵樹就要將之前的預測結果進行加強，也就是提升，所以針對的是第一棵樹還有多少沒有完成的量（彌補殘差）進行預測，這裡就是預測剩餘的50，假使第二棵樹預測值為30，然後就是將第一棵樹和第二棵樹看做一個整體，那麼第三棵樹的預測就是50-30=20，彌補前面所有的殘差，假使第三棵樹預測值為18，故最終的預測結果就是998
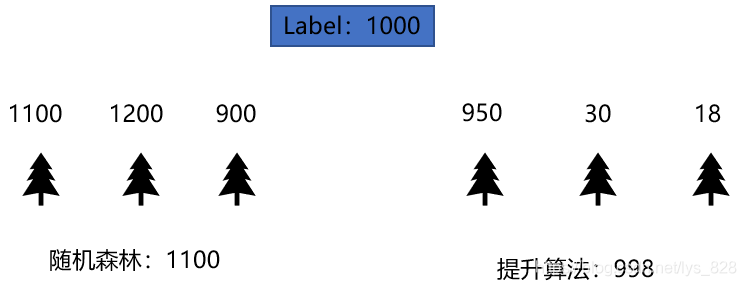
在這裡插入圖片描述

結合Boosting演演算法的公式理解：前面紅色框的就是前一輪的預測結果，後面藍色的是當前這一輪的，但是這一輪預測值往裡加是有一個前提的，要求加進來的樹是要讓模型比原來的強為準，體現在損失上就是加入這棵樹後損失是下降的。
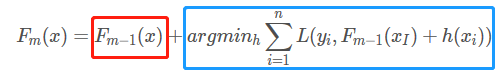
在這裡插入圖片描述
典型代表有：AdaBoost， Xgboost

其中的 Xgboost 就可以通過上面那個998的案例進行理解，而 AdaBoost 會根據前一次的分類效果調整資料權重，如果某一個資料在這次分錯了，那麼在下一次我就會給它更大的權重，最終每個分類器根據自身的準確性來確定各自的權重，再合體，完成結果，如下，後面也會詳細的通過程式碼進行介紹
在這裡插入圖片描述

四、堆疊模型簡述

Stacking模型，就是進行堆疊，很暴力，拿來一堆直接上（各種分類器都來了），對比串並聯電路，可以有不止一個串聯電阻和並聯電阻，反正套上就行（疊各種各樣的分類器KNN,SVM,RF等等），為了刷結果，不擇手段，多用於比賽刷分中，堆疊在一起確實能使得準確率提升，但是速度是個問題

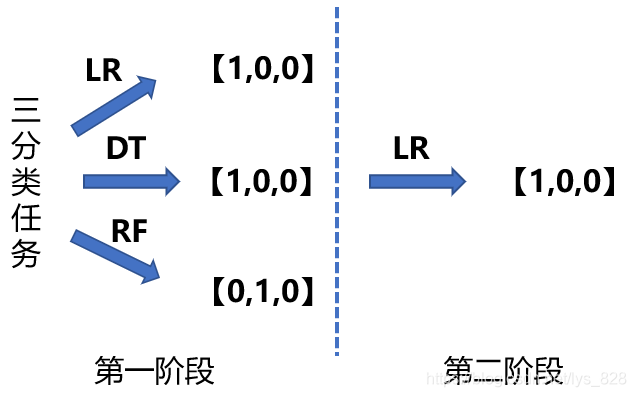
特徵：分階段進行，舉個例子（使用線性迴歸LR,決策樹DT,隨機森林RF進行堆疊），使用三個分類器進行三分類任務，進入第一階段分別使用三個分類器進行預測，結果為[1,0,0]，[1,0,0]，[0,1,0]，那麼接下來不是直接取這個預測結果的眾數或者均值，而是將第一階段的預測結果作為輸入，然後選擇分類器進入第二階段（假設選擇的是LR），圖示如下

在這裡插入圖片描述

五、硬投票和軟投票

1.概念介紹

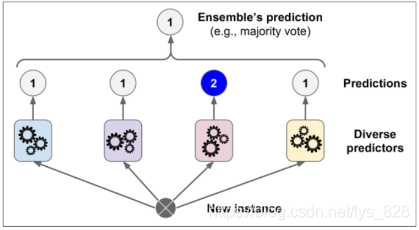
硬投票：就是隻拿最後的結果就事論事，如下，一組資料經過各個預測器後給出的結果分別是1,1,2,1，那麼最後的預測結果就是1（少數服從多數）
在這裡插入圖片描述
軟投票：就是考慮到各個分類器中的概率值進行加權平均。舉個例子進行說明，就是大學中上課老師點名的問題，A同學說，我覺得不會點吧（點名概率47%，以下都是假定），B同學說我上節課沒有去不太清楚點不點名（點名概率30%），C同學說已經兩次沒點了，應該會點名的，大家還是去吧（點名概率為97%），那麼基於這個結果，可以肯定還是要去上課的

2.硬投票程式碼實現

首先匯入相關的庫，然後載入需要使用的資料集

import warnings
warnings.filterwarnings('ignore')
import numpy as np
import os 
import matplotlib.pyplot as plt

from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split

#整合學習，這裡可以把資料量調大一下，比如選擇500個資料量，設定一些噪聲
X,y = make_moons(n_samples = 500, noise = 0.30, random_state = 42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 42)

#然後分別選取標籤為0和1的資料進行繪圖展示
plt.plot(X[:,0][y==0],X[:,1][y==0],'yo')
plt.plot(X[:,0][y==0],X[:,1][y==1],'bs')

輸出的結果為：
在這裡插入圖片描述
首先實現硬投票，可以參考一下官網的引數說明及範例，注意建立投票分類器中的voting引數，預設就是進行硬投票

範例實現如下

from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC

#建立多個分類器的範例
log_clf = LogisticRegression()
rnd_clf = RandomForestClassifier()
svm_clf = SVC() #支援向量機在之後的部落格中會更新，這裡拿來用一下

#構建投票分類器
voting_clf = VotingClassifier(estimators = [('lr',log_clf),('rf',rnd_clf),('svc',svm_clf)],voting = 'hard')

#訓練模型，可以只是看投票分類器的結果
#voting_clf.fit(X_train,y_train)

#也可以檢視所有分類器的結果，進行遍歷迴圈然後進行輸出結果即可
from sklearn.metrics import accuracy_score
for clf in (log_clf,rnd_clf,svm_clf,voting_clf):
    clf.fit(X_train,y_train)
    y_pred = clf.predict(X_test)
    print(clf.__class__.__name__,accuracy_score(y_test,y_pred))

輸出的結果為：（至此硬投票介紹完畢）

LogisticRegression 0.864
RandomForestClassifier 0.896
SVC 0.896
VotingClassifier 0.912

3.軟投票程式碼實現

接下來就是進行軟投票的程式碼實現，需要該改動的就是voting=‘soft’,另外由於軟投票針對的是概率值，SVC分類器中的引數probability預設是False，因此需要設定為True
在這裡插入圖片描述
實現程式碼如下：

from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC

log_clf = LogisticRegression(random_state = 42)
rnd_clf = RandomForestClassifier(random_state = 42)
svm_clf = SVC(random_state = 42, probability = True) #這裡需要修改一下probability引數

#修改一下voting引數
voting_clf = VotingClassifier(estimators = [('lr',log_clf),('rf',rnd_clf),('svc',svm_clf)],voting = 'soft') 

#剩下的不變
from sklearn.metrics import accuracy_score
for clf in (log_clf,rnd_clf,svm_clf,voting_clf):
    clf.fit(X_train,y_train)
    y_pred = clf.predict(X_test)
    print(clf.__class__.__name__,accuracy_score(y_test,y_pred))

輸出的結果為：（可以發現軟投票比硬投票的得分稍微好一些，靠譜一點）

LogisticRegression 0.864
RandomForestClassifier 0.896
SVC 0.896
VotingClassifier 0.92

六、Bagging策略效果

首先對訓練資料集進行多次取樣，保證每次得到的取樣資料都是不同的
分別訓練多個模型，例如樹模型（多采用決策樹）
預測時需得到所有模型結果再進行整合

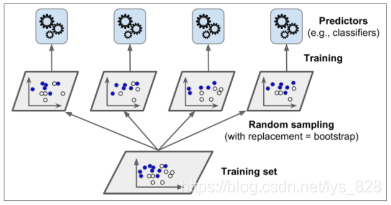
涉及有關引數的使用，可以檢視官方手冊，BaggingClassifier，實現的程式碼範例如下（對比一下有參和無參的區別）

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier

#如果直接使用決策樹模型
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train,y_train)
y_pred = tree_clf.predict(X_test)
accuracy_score(y_test,y_pred)
#這裡輸出的結果是0.856

#如果使用bagging模型
bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), #基本模型
    #n_estimators=10, 建立多少個樹，預設是10
    #max_samples=1.0,最大的樣本數
    #bootstrap=True，預設是隨機取樣
    n_jobs=-1,#平行計算
    random_state = 42
)

#這裡是什麼引數都不新增的
bag_clf.fit(X_train,y_train)
bag_pred = bag_clf.predict(X_test)
accuracy_score(y_test,bag_pred)
#此時輸出的結果為0.872

#如果稍微地調整一下預設的引數，如下
bag_clf_1 = BaggingClassifier(
    DecisionTreeClassifier(),
    n_estimators=500, #建立500棵樹
    max_samples=100,#樣本取100
    bootstrap=True,
    n_jobs=-1,
    random_state = 42
)
bag_clf_1.fit(X_train,y_train)
bag_pred = bag_clf_1.predict(X_test)
accuracy_score(y_test,bag_pred)
#此時輸出的結果為0.904

七、決策邊界視覺化展示

比如檢視一下整合與傳統方法的對比，關於繪製決策邊界的程式碼，封裝成函數，這裡就不再詳述了，可以網上找到很多，直接修改裡面一些引數即可出圖

from matplotlib.colors import ListedColormap #這裡匯入顏色包

#axes引數的取值根據上面繪製的影象的x,y軸的取值範圍確定，然後預設繪製等高線
def plot_decision_boundary(clf,X,y,axes=[-2,2,-1.5,2],alpha=0.5,contour=True):  
    x1s = np.linspace(axes[0],axes[1],100)
    x2s = np.linspace(axes[2],axes[3],100)
    x1,x2 = np.meshgrid(x1s,x2s)
    X_new = np.c_[x1.ravel(),x2.ravel()]
    y_pred = clf.predict(X_new).reshape(x1.shape)
    custom_cmp = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
    plt.contourf(x1,x2,y_pred,cmap = custom_cmp,alpha = 0.8)
    if contour:
        custom_cmp2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
        plt.contour(x1,x2,y_pred,cmap = custom_cmp2,alpha = 0.8)
    plt.plot(X[:,0][y==0],X[:,1][y==0],'yo',alpha=0.6)
    plt.plot(X[:,0][y==0],X[:,1][y==1],'bs',alpha=0.6)
    plt.axis(axes)
    plt.xlabel('x1')
    plt.ylabel('x2')

#建立畫布，分別建立兩個子圖進行展示
plt.figure(figsize=(12,5))
plt.subplot(121)
plot_decision_boundary(tree_clf,X,y)
plt.title('decide tree')
plt.subplot(122)
plot_decision_boundary(bag_clf,X,y)
plt.title('decide tree with bagging')

輸出的結果為：（可以看出經過bagging策略後決策的邊界要比普通的決策樹要平滑的多，也可以看到在左側的一些資料邊界是直接垂下來了，這部分資料分開的難度太大了，都幾乎融合在一塊了，所以最後模型只能是儘量的進行劃分多的資料）
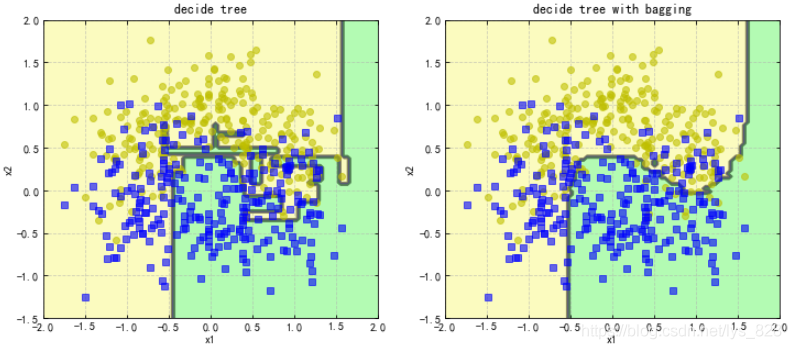
在這裡插入圖片描述

八、OOB袋外資料的作用

OOB策略：Out Of Bug，這個外是針對於bagging這個袋子而言的，bagging採取的隨機抽樣的方式去建立樹模型（可以參考一下隨機森林演演算法原理的圖示），那麼那些未被抽取到的樣本集，也就是未參與建立樹模型的資料集就是袋外資料集，我們就可以用這部分資料集去驗證模型效果，預設值為False，如果改變為True，就可以直接使用這部分資料進行檢測模型的可靠性，就不用再額外的做一些交叉驗證的操作了
在這裡插入圖片描述
實現的程式碼如下

bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), 
    n_estimators=500, 
    max_samples=100,
    bootstrap=True,
    n_jobs=-1,
    random_state = 42,
    oob_score=True #其餘的都不變，新增該引數
)

bag_clf.fit(X_train,y_train)
bag_clf.oob_score_ 
#模型訓練後，有oob_score_ 方法用來評估模型的得分

輸出的結果為：0.9253333333333333

而如果採用sklearn中封裝好的accuracy_score方法進行評估，程式碼如下：

y_pred = bag_clf.predict(X_test)
accuracy_score(y_test,y_pred)
#輸出結果為：0.904  比採用oob的資料評價的要低

九、特徵重要性視覺化展示

關於特徵重要性前面已經提及到，可以通過打亂或者破壞某個特徵從而檢視某個特徵的重要性，在整合學習中使用的幾乎都是樹模型，本身節點就代表著重要程度的大小，那麼具體要量化判斷的話，在sklearn中是看每個特徵的平均深度，也就是節點越往上，那麼這個特徵就越重要，反之就越不重要。這裡的資料首先使用鳶尾花資料集（資料較少，特徵也簡單），看一下輸出的特徵重要性是什麼樣的，程式碼如下

from sklearn.datasets import load_iris
iris = load_iris()
rf_clf = RandomForestClassifier(n_estimators=500,n_jobs=-1)
rf_clf.fit(iris['data'],iris['target'])
for name,score in zip(iris['feature_names'],rf_clf.feature_importances_):
    print (name,score)
    plt.barh(name,score)

輸出的結果為：（後面的數值就代表這平均深度的取值，說明花瓣的長度和寬度對模型的分類很重要）
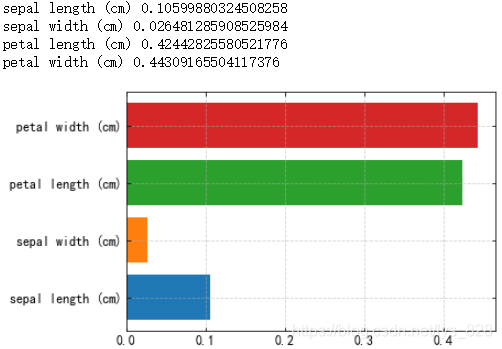
在這裡插入圖片描述
然後再載入較為複雜的資料，這裡以手寫數位集（mnist資料）為例，就可以通過繪製熱度圖進行展示

from sklearn.datasets import fetch_openml
mnist = fetch_openml('MNIST_784') #第一次載入的時候會花一點時間，30s左右

#使用隨機森林建立500棵樹
rf_clf = RandomForestClassifier(n_estimators=500,n_jobs = -1)
rf_clf.fit(mnist['data'], mnist['target'])

#rf_clf.feature_importances_.shape
#可以檢視一下訓練後的特徵的形狀為28*28=784，共有784個畫素點

#繪製熱度圖顯示特徵重要性
import matplotlib
def plot_digit(data):
    image = data.reshape(28,28)
    plt.imshow(image,cmap = matplotlib.cm.hot)
    plt.axis('off')

plot_digit(rf_clf.feature_importances_)
#重要的提示，可以通過顏色欄檢視特徵重要度的分佈
char = plt.colorbar(ticks = [rf_clf.feature_importances_.min(),rf_clf.feature_importances_.max()])
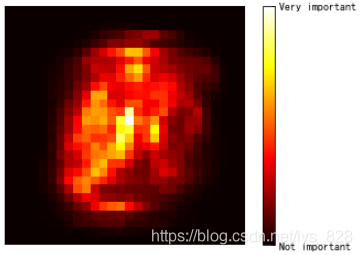
char.ax.set_yticklabels(['Not important','Very important'])

輸出的結果為：（右側的顏色條不能搞掉了，不然不清楚哪部分割區域是屬於特徵重要的部分，在手寫資料集中只用中間才有數位，周圍都是白底，所以越往兩邊特徵越不重要）
在這裡插入圖片描述

十、AdaBoost演演算法決策邊界展示

前面簡單的提到了AdaBoost演演算法，類別於串聯電路，功能是一步步進行累加的。舉個例子進行理解，就是初高中時候做題或者考試的時候，會有一個錯題本，每次將裡面的難題或者易錯的題收集起來，多看多練習，下次在遇到的時候就不會做錯了。Adaboost演演算法就是一樣的道理，在建立每一個模型的時候就會想一想上一次訓練的時候哪一些樣本沒有做好，那麼這次就得額外重視一下還沒有做好的樣本資料。

在AdaBoost中有一個 樣本的權重項 ，因此之後在往模型中輸入資料的時候就不會都是同樣的權重了，如下圖示，最初的時候是相同的權重，模型訓練後出現問題後，進行權重的調整，如果還出現問題，繼續進行權重的調整（沒有問題的資料權重調的小一些，有問題的資料權重調的大一些），這樣每次調整之後就會有一個準確率，最後的結果就是加權平均，假如下圖的上面三個結果（ABC）分別有90%、80%、50%的準確度，那麼最終的結果就是0.9A+0.8B+0.5C。
在這裡插入圖片描述
以SVM分類器為例來演示AdaBoost的基本策略（這裡就是展示AdaBoost是怎麼一步步實現的）

from sklearn.svm import SVC #重新匯入一下，這裡先用一下，後面更新的博文會詳細介紹

m = len(X_train) #計算資料的長度

plt.figure(figsize=(14,5))
#建立兩個子圖， 不同的學習率
for subplot,learning_rate in ((121,1),(122,0.5)):
    sample_weights = np.ones(m)#設定的初始權重都為1
    plt.subplot(subplot) 
    #進行五次結果權重的調整
    for i in range(5):
        svm_clf = SVC(kernel='rbf',C=0.05,random_state=42) #建立模型
        svm_clf.fit(X_train,y_train,sample_weight = sample_weights) #訓練模型
        y_pred = svm_clf.predict(X_train)#然後計算預測值
        sample_weights[y_pred != y_train] *= (1+learning_rate) #根據預測值和真實值的差值進行權重的調整
        plot_decision_boundary(svm_clf,X,y,alpha=0.2)#顯示每次調整的邊界
    plt.title('learning_rate = {}'.format(learning_rate))#列印標題
    #這裡就是對決策邊界標一下號
    if subplot == 121:
        plt.text(-0.7, -0.65, "1", fontsize=14)
        plt.text(-0.6, -0.10, "2", fontsize=14)
        plt.text(-0.5,  0.10, "3", fontsize=14)
        plt.text(-0.4,  0.55, "4", fontsize=14)
        plt.text(-0.3,  0.90, "5", fontsize=14)
plt.show()

輸出結果為：（最後的標記數值，就可以顯示AdaBoost每次調整的結果，以上程式碼是屬於手寫程式碼進行AdaBoost的基本策略的演示，實際上可以直接使用sklearn封裝好的模組進行模型建立）
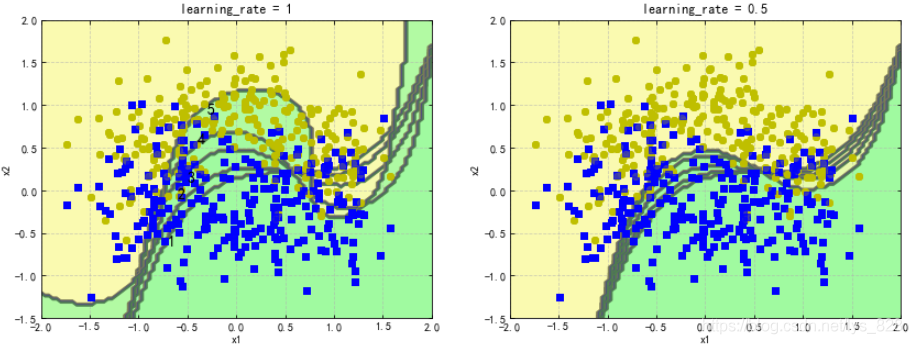
在這裡插入圖片描述
使用sklearn中的AdaBoostClassifier分類器建立模型，程式碼如下，幾乎和其他模型建立的過程一致，主要在於設定分類器中的引數

from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), #為了更好的展示最後的分界，這裡設定樹的深度為1
                   n_estimators = 200,
                   learning_rate = 0.5,
                   random_state = 42
)

ada_clf.fit(X_train,y_train)
plot_decision_boundary(ada_clf,X,y)

輸出的結果為：（直接將最終的結果展示出來）
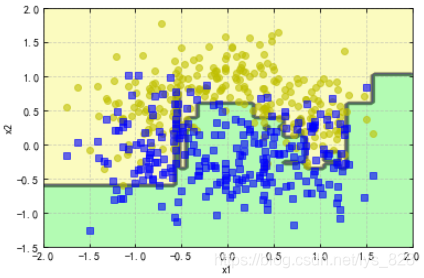
在這裡插入圖片描述

十一、Gradient Boosting梯度提升演演算法

也就是之前舉得998範例，基於此演演算法共有三個版本，最初的GBDT,後來發展到了XGBoost和最新的LightGBM,這裡就介紹一下最初的GBDT提升演演算法的基本流程，後面兩個演演算法也是基於同一原理，會在之後的實際案例中會進行展示。

首先指定一下資料，然後就是依次傳入資料，建立模型並訓練模型，最後是進行整體模型的預測

np.random.seed(42)
X = np.random.rand(100,1) - 0.5 #X變數是列表巢狀的
y = 3*X[:,0]**2 + 0.05*np.random.randn(100)

#建立迴歸樹模型
from sklearn.tree import DecisionTreeRegressor
#開始建立第一個樹並進行訓練
tree_reg1 = DecisionTreeRegressor(max_depth = 2)
tree_reg1.fit(X,y)

#然後使用殘差進行第二棵樹的建立和訓練
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth = 2)
tree_reg2.fit(X,y2)

#同理進行第三棵樹的建立和訓練
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth = 2)
tree_reg3.fit(X,y3)

#最後計算預測的結果，即為所有模型結果之和
X_new = np.array([[0.8]]) #假使預測資料x為0.8
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1,tree_reg2,tree_reg3))
y_pred

輸出結果為：array([0.75026781])

為了方便理解，這裡可以進行圖示的視覺化操作，程式碼如下

def plot_predictions(regressors, X, y, axes, label=None, style="r-", data_style="b.", data_label=None):
    x1 = np.linspace(axes[0], axes[1], 500)
    y_pred = sum(regressor.predict(x1.reshape(-1, 1)) for regressor in regressors)
    plt.plot(X[:, 0], y, data_style, label=data_label)
    plt.plot(x1, y_pred, style, linewidth=2, label=label)
    if label or data_label:
        plt.legend(loc="upper center", fontsize=16)
    plt.axis(axes)

plt.figure(figsize=(11,11))

plt.subplot(321)
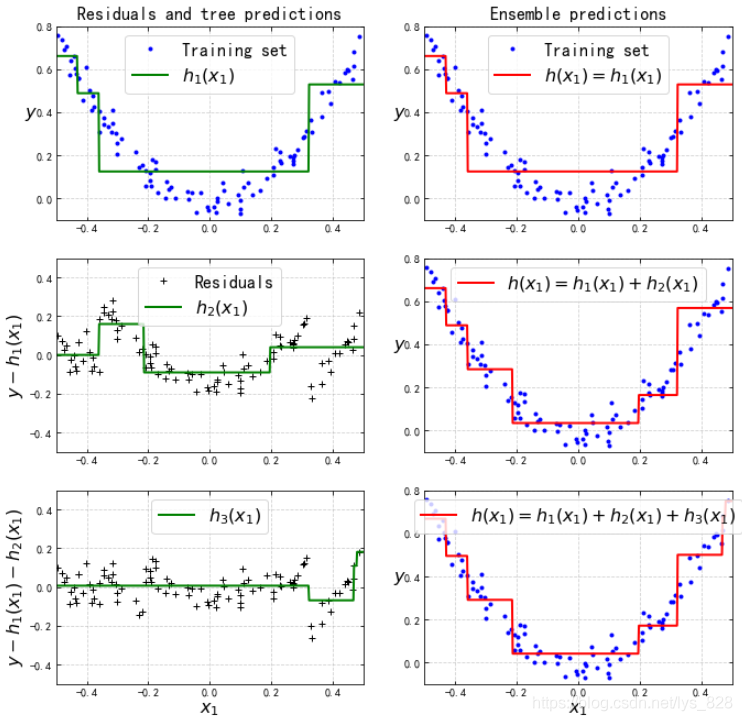
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h_1(x_1)$", style="g-", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Residuals and tree predictions", fontsize=16)

plt.subplot(322)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1)$", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)

plt.subplot(323)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_2(x_1)$", style="g-", data_style="k+", data_label="Residuals")
plt.ylabel("$y - h_1(x_1)$", fontsize=16)

plt.subplot(324)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.ylabel("$y$", fontsize=16, rotation=0)

plt.subplot(325)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_3(x_1)$", style="g-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)

plt.subplot(326)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)

plt.show()

輸出結果為：（可以發現隨著決策樹數量的增多，資料殘差越來越像0進行靠近，然後x與y的擬合曲線也越來越接近真實的資料）
在這裡插入圖片描述

十二、整合引數對比分析

以上是手動自己敲程式碼實現的GBDT策略的流程，其實在sklearn中已經封裝好了GBDT，可以參考官網給出的GradientBoostingRegressor分類器，實現的程式碼如下，這裡主要是分析整合引數不同對模型的影響

from sklearn.ensemble import GradientBoostingRegressor

#建立一個基礎樹
gbrt = GradientBoostingRegressor(max_depth = 2,
                          n_estimators = 3,
                          learning_rate = 0.1,
                          random_state = 41
)
gbrt.fit(X,y)

#在第一棵樹的基礎上修改學習率：0.1——>1
gbrt_slow_1 = GradientBoostingRegressor(max_depth = 2,
                          n_estimators = 3,
                          learning_rate = 1.0,
                          random_state = 41
)
gbrt_slow_1.fit(X,y)

#在第一棵樹的基礎上修改樹的個數：3——>200
gbrt_slow_2 = GradientBoostingRegressor(max_depth = 2,
                          n_estimators = 200,
                          learning_rate = 0.1,
                          random_state = 41
)
gbrt_slow_2.fit(X,y)

最後進行兩兩分析，首先選擇不同學習率的模型進行對比

#最後進行兩兩對比分析
plt.figure(figsize = (12,4))
plt.subplot(121)
plot_predictions([gbrt],X,y,axes=[-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate={},n_estimators={}'.format(gbrt.learning_rate,gbrt.n_estimators))

plt.subplot(122)
plot_predictions([gbrt_slow_1],X,y,axes=[-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate={},n_estimators={}'.format(gbrt_slow_1.learning_rate,gbrt_slow_1.n_estimators))

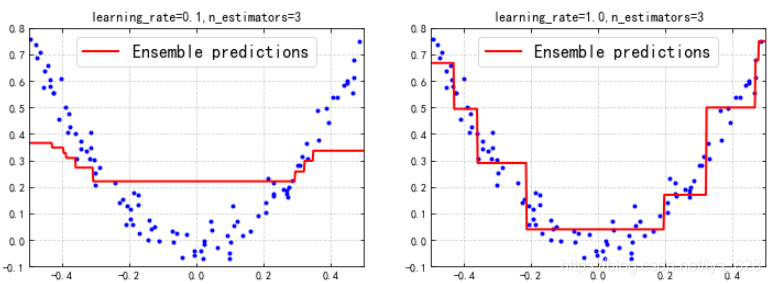
輸出結果為：（第二個模型與第一個模型的對比分析，差別在學習率上，這裡的學習率是指每次建立樹後使用時的權重，一般不是全部使用整個樹模型，防止過擬合，可以發現由於只建立了三個樹，預設的學習率為0.1，也就是每次加進來的樹只用了其中的0.1，導致最終的模型效果很差，而第二個模型學習率為1，說明加進來的樹全部都利用上了，最後的擬合結果比較不錯，因此給的啟發就是在建立的樹比較少時應該提高學習率，以便充分利用每次加進來的樹模型）
在這裡插入圖片描述
其次選擇不同樹的數量進行對比分析

plt.figure(figsize = (12,4))
plt.subplot(121)
plot_predictions([gbrt],X,y,axes=[-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate={},n_estimators={}'.format(gbrt.learning_rate,gbrt.n_estimators))

plt.subplot(122)
plot_predictions([gbrt_slow_2],X,y,axes=[-0.5,0.5,-0.1,0.8],label = 'Ensemble predictions')
plt.title('learning_rate={},n_estimators={}'.format(gbrt_slow_2.learning_rate,gbrt_slow_2.n_estimators))

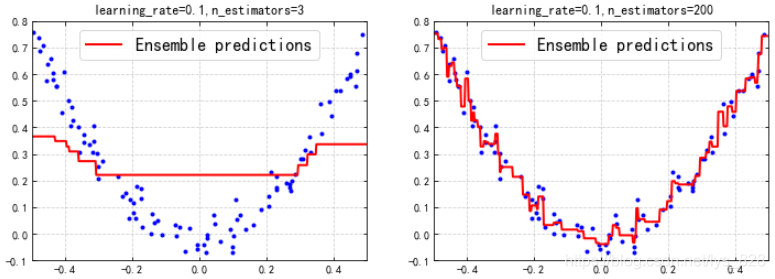
輸出結果為：（不用多說，理論上只要樹的數量足夠多，最後的模型擬合結果一定會照顧到每一個點的，所以當樹的數量為200時候呈現了很好的擬合效能，雖然此時的學習率為預設的0.1，此次對比就告訴我們今後在建立整合學習模型時候樹的數量要足夠多的，一般是在100棵往上）
在這裡插入圖片描述

十三、提前停止策略

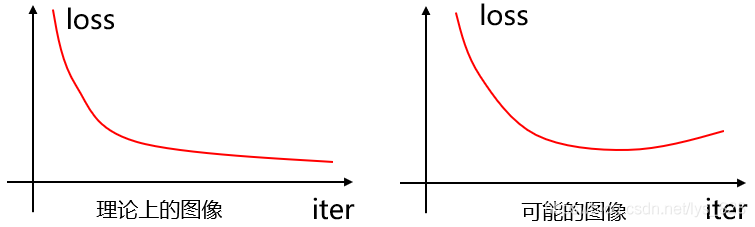
為什麼會出現提前停止的策略呢？理論上來講模型迭代的次數越多，最終的損失值loss越小，反應在影象中就應該是如下的左側曲線，但是實際上的曲線並不一定是這樣的，可能在迭代的某一次時候發生了loss值的回升或者波動，因此就需要進行提前停止，獲取最佳的迭代次數（最佳引數）

在這裡插入圖片描述

比如我們在執行大樣本資料的預測時候，往往會進行分階段進行模型資料的儲存，假使有10w條資料，那麼在模型跑到5w之後就可能每過1w條資料就進行儲存一下，方便檢視一下模型，這就需要分階段進行預測了，在sklearn中提供了這個功能，staged_predict函數，分階段進行預測
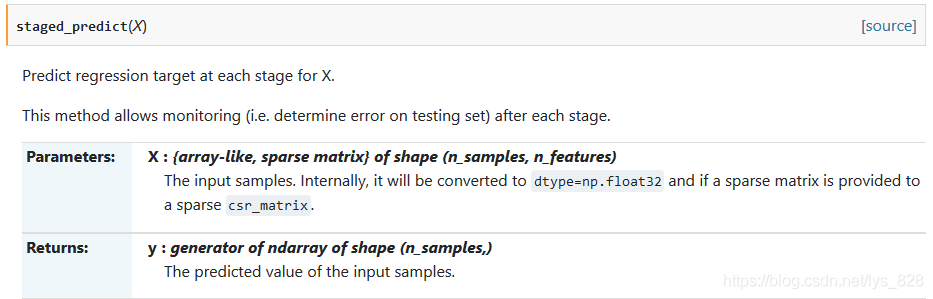
在這裡插入圖片描述
程式碼實現如下：

from sklearn.metrics import mean_squared_error
X_train,X_val,y_train,y_val = train_test_split(X,y,random_state=49)
gbrt = GradientBoostingRegressor(max_depth = 2,
                          n_estimators = 120,
                          random_state = 42
)
gbrt.fit(X_train,y_train)

errors = [mean_squared_error(y_val,y_pred) for y_pred in gbrt.staged_predict(X_val)] #得到所有的誤差
bst_n_estimators = np.argmin(errors) + 1  #求解出最佳的決策樹數量，注意errors列表，這裡使用np返回最小值的索引，對應的實際上的決策樹數量應該是+1的，這一點可以在後面的for迴圈判斷何時進行停止的時候進行驗證

gbrt_best = GradientBoostingRegressor(max_depth = 2,
                          n_estimators = bst_n_estimators, #這裡將最合適的數量進行賦值
                          random_state = 42
)
gbrt_best.fit(X_train,y_train) #使用最佳的決策樹數量建立模型並訓練

#可以檢視一下最小的損失值
#min_error = np.min(errors)
#min_error 此時為0.002712853325235463

#繪製一下出現轉折點的情況，並把最佳引數時對應的圖形繪製出來
plt.figure(figsize = (11,4))
plt.subplot(121)
plt.plot(errors,'b.-')
plt.plot([bst_n_estimators,bst_n_estimators],[0,min_error],'k--') #繪製豎線
plt.plot([0,120],[min_error,min_error],'k--')#繪製橫線
plt.axis([0,120,0,0.01]) #為了清楚顯示，將刻度值再分的細一些
plt.title('Val Error')

plt.subplot(122)
plot_predictions([gbrt_best],X,y,axes=[-0.5,0.5,-0.1,0.8]) #利用之前已經封裝的函數可以直接出圖
plt.title('Best Model(%d trees)'%bst_n_estimators)

輸出的結果為：（可以看到實際的情況正如剛剛說的一樣，會出現轉折點的情況，在55棵樹的時候模型已經到達了最佳效果，再往後就越來越差了）
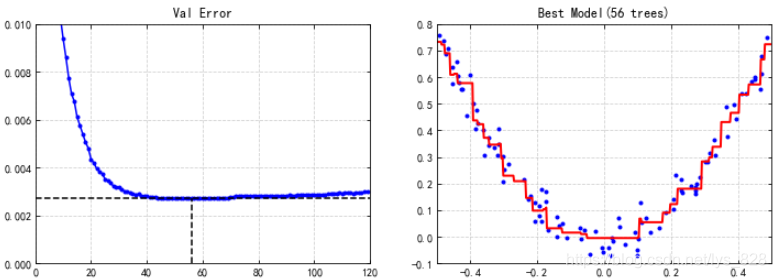
在這裡插入圖片描述

也可以判斷何時跳出for迴圈，這裡假定連續出現五次預測的結果損失比上一次高就為跳出的點，那麼書寫程式碼如下：（有個小問題就是，要實現1-120棵樹，每個數值對應的模型都要訓練一次，如果直接就上來硬鋼的話，也不是不可以，有沒有更好的方法，比如在訓練完3棵樹後，想要訓練4棵樹的時候就在第三棵樹的基礎上進行？辦法總是有的，裡面的引數warm_start=True就是為了解決這個問題，減少重複的勞動和模型執行的時間）

gbrt = GradientBoostingRegressor(max_depth = 2,
                             random_state = 42,
                                 warm_start =True #
)
error_going_up = 0
min_val_error = float('inf') #因為要判斷最小值，要有一個比較的物件，首先初始化為無窮大

for n_estimators in range(1,120):
    gbrt.n_estimators = n_estimators
    gbrt.fit(X_train,y_train)
    y_pred = gbrt.predict(X_val)
    val_error = mean_squared_error(y_val,y_pred)
    if val_error < min_val_error: #如果比前一個數值小的話
        min_val_error = val_error #那麼最小值自然也就發生變化了
        error_going_up = 0 
        print(min_val_error,n_estimators) #這個print語句就是驗證上方的bst_n_estimators對應的數值的
    else:
        error_going_up +=1
        if error_going_up == 5: #如果當前模型的損失比上一輪還高的現象出現了五次，那麼就跳出迴圈
            break

因此就可以找到最佳的決策樹數量，如下：
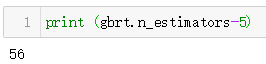
在這裡插入圖片描述

十四、堆疊模型

該模型並沒有前面講解的兩種模型使用的廣，前面已經進行了簡述了，這裡就給出過程圖，和之前的原理類似
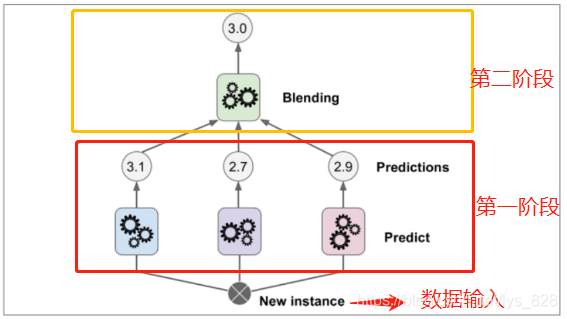
在這裡插入圖片描述
程式碼實現如下：（仍舊使用之前的手寫資料集，然後使用幾個暫未學習到的分類器，這裡只是拿來湊數，之後的部落格中會有介紹）

from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_openml
mnist = fetch_openml('MNIST_784')

#劃分資料
X_train_val, X_test, y_train_val, y_test = train_test_split(
    mnist.data, mnist.target, test_size=10000, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(
    X_train_val, y_train_val, test_size=10000, random_state=42)

#引入不同的分類器，這裡最後（第二階段）使用的就是本文介紹的隨機森林分類器，其他的湊數即可
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.svm import LinearSVC
from sklearn.neural_network import MLPClassifier

#各分類器進行範例化，注意初始狀態要一致
random_forest_clf = RandomForestClassifier(random_state=42)
extra_trees_clf = ExtraTreesClassifier(random_state=42)
svm_clf = LinearSVC(random_state=42)
mlp_clf = MLPClassifier(random_state=42)

#為了簡潔程式碼，將各個分類器的範例裝在列表中，之後建立for迴圈直接就可以全部進行訓練了
estimators = [random_forest_clf, extra_trees_clf, svm_clf, mlp_clf]

#依次進行模型訓練
for estimator in estimators:
    print("Training the", estimator)
    estimator.fit(X_train, y_train)

#建立陣列存放各個模型預測後的結果，方便下一階段作為資料輸入
X_val_predictions = np.empty((len(X_val), len(estimators)), dtype=np.float32) #根據資料和分類器數量的維度建立空陣列

for index, estimator in enumerate(estimators):
    X_val_predictions[:, index] = estimator.predict(X_val) #依次遍歷四種分類器，將最終預測的結果加入到陣列中
    
X_val_predictions #檢視陣列

輸出的結果為：

array([[5., 5., 5., 5.],
       [8., 8., 8., 8.],
       [2., 2., 2., 2.],
       ...,
       [7., 7., 7., 7.],
       [6., 6., 6., 6.],
       [7., 7., 7., 7.]], dtype=float32)

將該陣列直接用來作為輸入資料進入第二階段，然後使用熟悉的隨機森林模型進行訓練後就可以獲得模型最終的得分

rnd_forest_blender = RandomForestClassifier(n_estimators=200, oob_score=True, random_state=42)
rnd_forest_blender.fit(X_val_predictions, y_val)
rnd_forest_blender.oob_score_  #前面加了oob_score引數這裡直接就可以獲得模型的評估分數

輸出結果為：0.9681

至此關於整合演演算法的全部內容就梳理完畢了！撒花✿✿ヽ(°▽°)ノ✿

總結

本文介紹了整合學習演演算法的三種主要的模型，將概念以通俗易懂的例子入手進行講解，並配合上之後的程式碼應用講解，以及結果的視覺化，最主要的就是完成了整合學習相關知識點的詳細梳理，打通了任督二脈，不足之處是對於有些知識點文章中只是涉及沒有具體展開，這些會在之後的博文中進行講解

【機器學習16】整合學習及演演算法詳解

整合學習及演演算法詳解

前言