數位通訊系統簡易通道編碼模擬與效能分析

行動通訊普遍存在干擾與衰落的問題，這些問題會導致訊號收發雙方的資訊差錯，因此有必要增強資料在通道中傳輸時抵禦各種干擾的能力，提高系統的可靠性，對要在通道中傳送的數位訊號進行的糾錯檢錯編碼的過程就是通道編碼。

通道編碼是無線通訊過程中一個重要技術，因此筆者構建了一個簡易數位通訊系統，對其進行探究性學習，並通過MATLAB模擬對其通道編碼過程的效能進行分析。

一、系統架構

系統架構如下圖1-1所示。

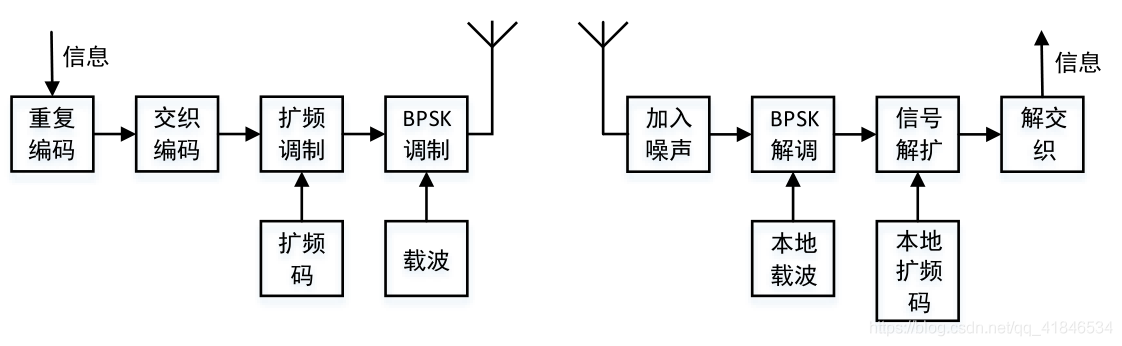
圖1-1 系統架構框圖

模擬設計的通道編碼過程主要包含重複編碼、交織編碼、擴頻、BPSK調變以及相應的通道譯碼等等，對不同編碼處理模組進行相應的訊雜比-誤位元速率等效能分析。

二、效能分析

2.1 重複編碼
重複編碼的作用主要是提升糾錯能力，將信源訊號進行重複編碼就是將訊號的序列量加倍傳輸，設重複編碼後序列

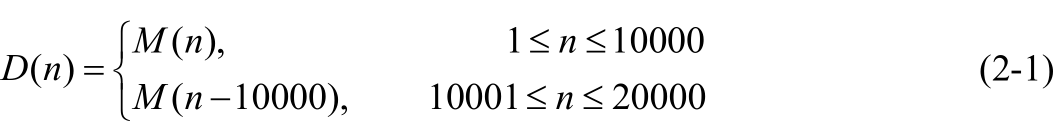
其中$D(n)$是原始序列$M(n)$重複兩次後的序列，則重複編碼後序列的碼元傳輸速率將變為原始序列的二分之一，以犧牲傳輸效率的代價，提升了糾錯能力。原始序列與重複編碼後序列在AWGN(Additive White Gaussian Noise，加性高斯白噪聲)中的效能比較如下圖2-1所示。

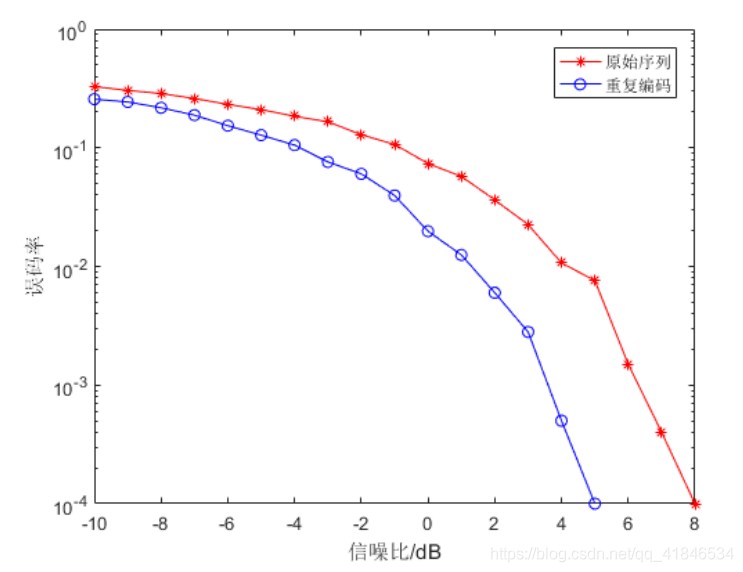
圖2-1 原始序列與重複編碼傳輸SNR-BER關係曲線比較

由曲線關係圖可知，當訊雜比在-10dB至10dB區間內，重複編碼後序列在訊雜比5dB時誤位元速率就已達到$10^{-4}$，而相同誤位元速率下原始序列訊雜比需要達到8dB，由此可見序列經過重複編碼後在AWGN中的誤位元速率更低。同時隨著訊雜比的減小，重複編碼降低誤位元速率的效能越優。

2.2 交織編碼與解交織
交織編碼技術作為一種編碼新技術，主要用於有記憶的通道，特別是無線通道，以此來糾正成串發生的位元差錯和一些突發錯誤。交織編碼實際上是兩個過程：交織與FEC(Forward Error Correction，向前錯誤更正)，實際輸入序列前後是具有一定的相關性的，而交織主要起到解相關的作用，通過提升序列的隨機性來提高資訊量。筆者選擇分組交織作為信源編碼的交織過程，圖2-2較為形象地體現了分組交織的作用。

圖2-2 分組交織實現成串差錯離散化過程

由上圖可知，8個序列經過分組交織——按行寫入、按列讀出後，原本三個連續差錯序列被成功分開，使得接收機能夠有效讀取序列。而針對上文經過重複編碼後的序列，利用交織矩陣對序列進行相應處理，觀察是否可以離散其成串差錯。

設輸入序列函數$D_{in}(t)=D(n)=(n_1,n_2,n_3,...,n_{19999},n_{20000})$，將重複編碼後的序列通過交織編碼器，將需要傳送的一段資訊放入，形成按列寫入、按行讀出的交織矩陣 （200行，100列）。

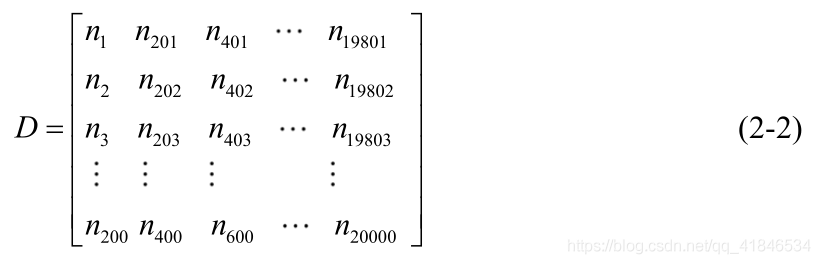
交織器輸出資訊為$D_{out}(n)=(n_1,n_{201},n_{401},n_{601},...,n_{19600},n_{19800},n_{20000})$，假設出現突發錯誤，輸出資訊$D_{error}(n)=(\overline{n_1},\overline{n_{201}},\overline{n_{401}},\overline{n_{601}},...,\overline{n_{19600}},\overline{n_{19800}},\overline{n_{20000}})$。

在接收端進行解交織操作，形成一個按行寫入、按列讀出的交織矩陣。

交織器輸出資訊$L(n)=(\overline{n_1},n_2,n_3,...,\overline{n_{601}},...,n_{19999},\overline{n_{20000}})$。

可以看到，最終成串的位元差錯成為隨機獨立差錯，一定程度上提升了本系統資訊傳輸的可靠性，與圖2-2中離散成串差錯的功能一致。

原始序列與分組交織後序列在AWGN(Additive White Gaussian Noise，加性高斯白噪聲)中的效能比較如下圖2-3所示。

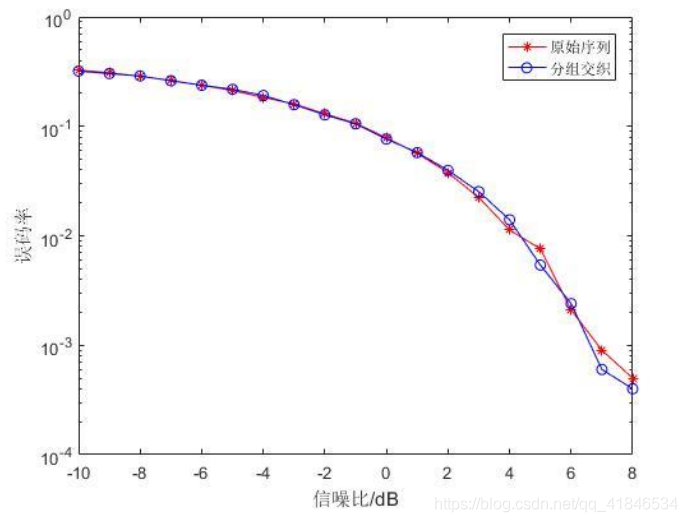
圖2-3 原始序列與交織編碼SNR-BER關係曲線比較

由圖可知，兩種情況下的誤位元速率是無法區分高低的，原因在於分組交織作為信源編碼的一種，僅僅起到將成串差錯離散成隨機差錯的作用，無法降低誤位元速率，同時輸入序列本身就為隨機序列，經過交織後無法提升其隨機性，因此會出現原始序列與分組交織後序列訊雜比-誤位元速率關係曲線基本一致的情況。

2.3 擴頻調變解調
擴頻，即擴充套件頻譜通訊，是一種資訊傳輸方式，其訊號所佔有的頻頻寬度遠大於所傳資訊必需的最小頻寬。而頻帶的擴充套件則是通過一個獨立的碼序列來完成並用編碼及調變的方法來實現的，與所傳資訊資料無關。在接收端則需要用同步的碼序列進行擴頻解調的操作。

直接序列擴頻通訊具有頻譜寬、工作訊雜比低、抗干擾和抗多徑效應能力強、可實現分碼多重進接、低截獲和低檢測概率等特點。因此筆者將採用直接序列擴頻技術，利用WALSH碼作為系統中的擴頻碼，實現擴頻調變的操作。WALSH函數是一種非正弦的完備正交函數系，僅有$＋1$和$－1$兩種可能取值，比較適合用來表達和處理數位訊號，也方便後續BPSK調變以及接收機解調等操作。

設擴頻處理增益為$G_p$，則有

其中，$T_b$為輸入資訊碼元寬度，$T_p$為擴頻碼碼元寬度。不妨設輸入資訊碼元寬度為擴頻碼碼元寬度的10倍，即擴頻處理增益$G_p=10dB$ ，設擴頻碼為雙極性序列 C ( n ) = { − 1 , + 1 } C(n)=\{{-1,+1}\} C(n)={−1,+1}，同時將交織編碼後的單極性序列$D_{out}(n)$轉為雙極性序列$D^{\ast }(n)$，由上文編碼過程分析可得其中$1\le n\le 20000$。

由於建立的模型為簡易數位通訊系統，因此從數位的角度出發對於訊號進行一系列處理，以擴頻處理增益$G_p=10dB$為例，則擴頻碼$C(n)$中每1組（1組10個）擴頻序列都要與$D^{\ast }(n)$中對應的每個序列做互斥或運算，邏輯運算過程如下圖2-4所示。

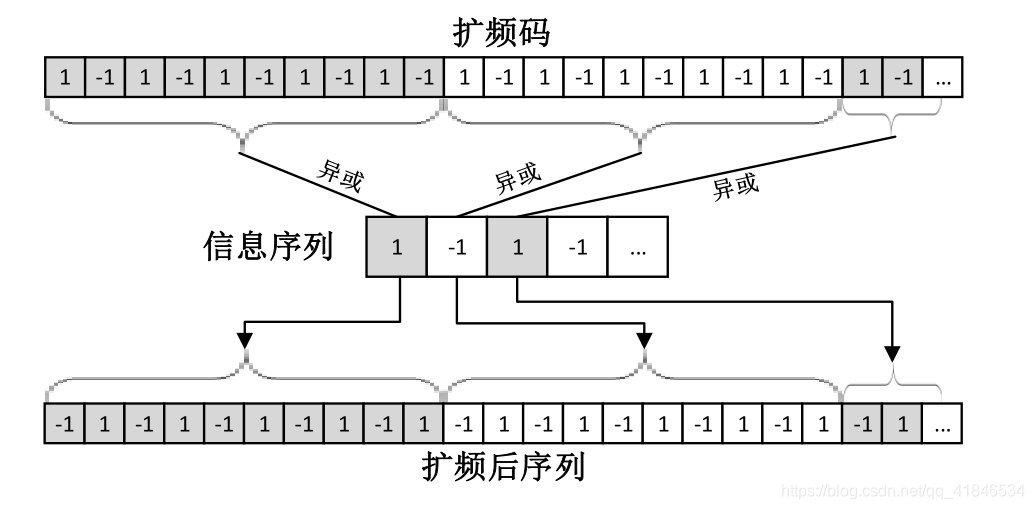
圖2-4 擴頻序列對資訊序列的擴頻調變過程

在上述邏輯運算過程中，不難發現序列的擴頻過程一定程度上具有重複編碼的效能。擴頻碼對資訊序列調變的過程，實際上也可以看作將資訊序列重複10次後與擴頻碼進行互斥或運算；而在接收端的解擴處理則直接將接收訊號與同頻擴頻碼進行互斥或運算處理，將序列恢復成與輸入序列數量一致的輸出序列，有效地降低了系統誤位元速率，提升糾錯能力。

則原始序列與擴頻後序列在AWGN(Additive White Gaussian Noise，加性高斯白噪聲)中的效能比較如下圖2-5所示。

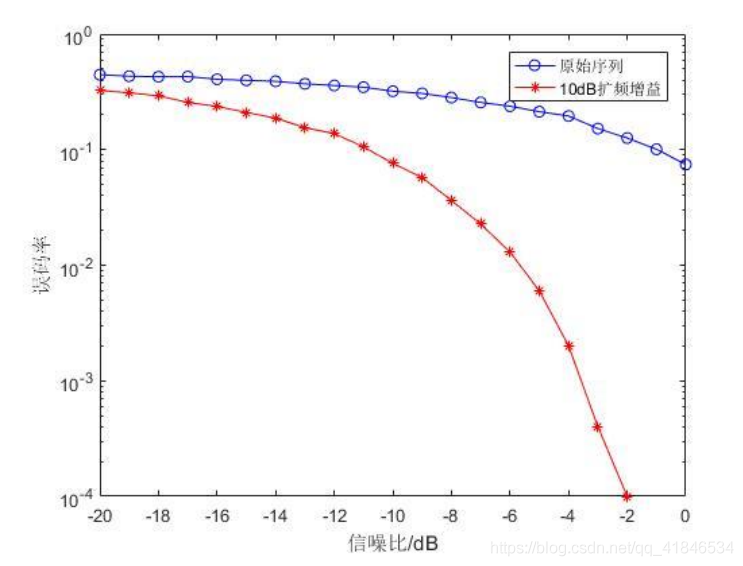
圖2-5 原始序列與擴頻序列SNR-BER關係曲線比較

由圖可知，經過10dB擴頻處理增益對應擴頻調變解調後，在訊雜比-20dB至0dB的AWGN環境下，經過10dB擴頻、解擴後的序列誤位元速率遠小於未經擴頻處理的序列，同時，在-10dB訊雜比下經過擴頻調變解調序列誤位元速率與0dB訊雜比下未經擴頻處理序列誤位元速率基本相同，這樣的結果與設定的擴頻處理增益$G_p=10dB$ 相一致。較前期的重複編碼、交織編碼而言，擴頻調變降低誤位元速率的效能（即糾錯能力）最優。

2.4 BPSK調變解調
BPSK，即二相移相鍵控。BPSK訊號具有頻帶利用率高、頻寬小、抗干擾性好等諸多優點，在分碼多重進接通訊中最為常用。因為直接序列擴頻存在傳輸失真、傳輸損耗以及無法保證帶內特性，所以為了進行長途傳輸，基頻訊號需要通過載波調變將頻譜搬移到適合無線通道傳輸的特定頻帶處。因此在直接序列擴頻通訊中，通常採用的調變方式是BPSK。

在BPSK中，通常使用初始相位0表示二進位制序列0，初始相位$\pi$表示二進位制序列1，由此可以的到BPSK訊號時域表示式

其中，$A$為訊號幅度，${\omega }_c$為載波頻率，${\phi }_n$表示第$n$個符號的絕對相位，即

因此，式(2-6)可表示為

由於表示訊號的兩種碼元波形相同、極性相反，因此BPSK訊號可以表示為一個雙極性矩形脈衝序列（全佔空）與一個正弦載波相乘後的訊號，即

其中

這裡$g(t)$為脈寬為$T_B$的單個矩形脈衝。$a_n$的統計特性為

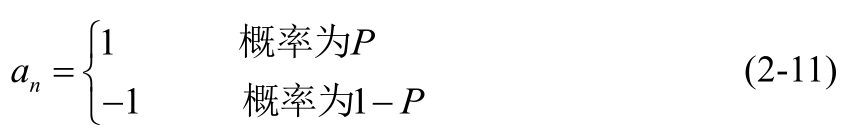
以上以載波不同相位直接表示相應二進位制數位訊號的調變方式，稱為二進位制絕對相移鍵控。

在AWGN通道下，BPSK訊號經過相干解調後理論誤位元速率為

其中，$r$為訊雜比（無單位）。將模擬過程中$1\times 10^4$個序列未載入波的模擬誤位元速率與理論誤位元速率進行比較，得到圖2-6所示曲線圖。

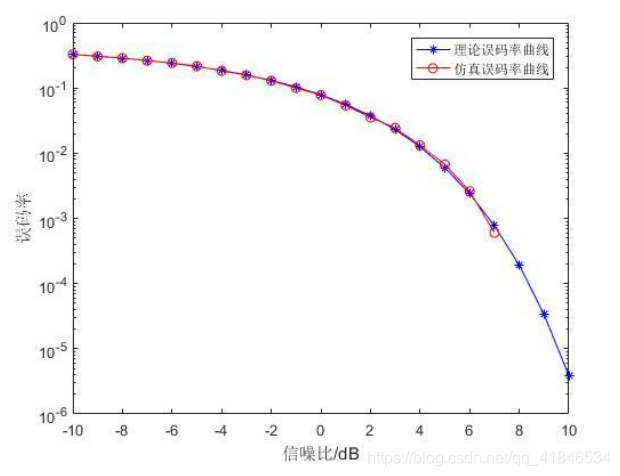
圖2-6 BPSK理論BER與模擬BER曲線比較

由上圖可以看出，對於$1\times 10^4$個序列在1dB至10dB的訊雜比下的BPSK調變解調，理論誤位元速率與模擬誤位元速率是基本一致的，同時誤位元速率普遍較低。

2.5 通道衰減
對於此類通訊系統研究，往往將直射波損耗作為傳輸損耗。在自由空間中，電波沿直線傳播直接到達接收點，不被吸收、不發生反射、折射和散射現象而的傳播方式稱為直射波傳播。直射波傳輸損耗可以看成是自由空間的電波傳播損耗

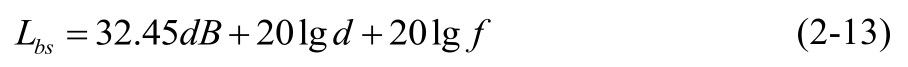
其中，$d$為傳輸距離(km)，$f$為訊號工作頻率(MHz)。當傳輸距離或訊號工作頻率任一引數不變，另一引數改變時，直射波損耗也隨之發生相應的對數變化，相應變化曲線圖如下圖2-7、圖2-8所示。

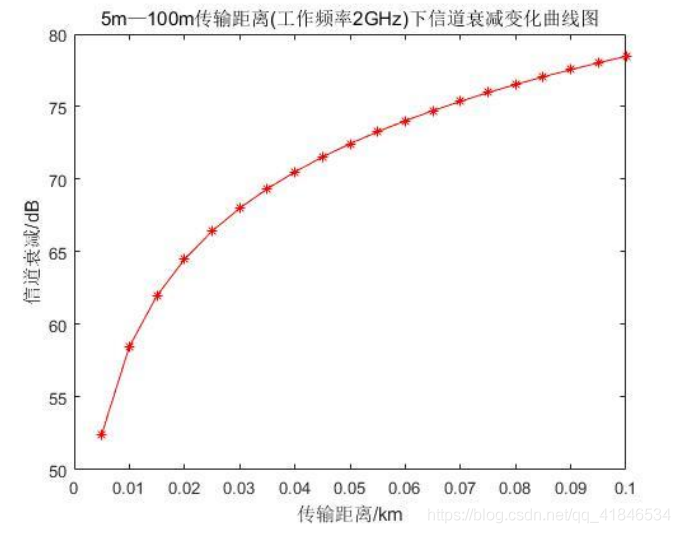
圖2-7 5m-100m傳輸距離（工作頻率2GHz）下通道衰減變化曲線圖

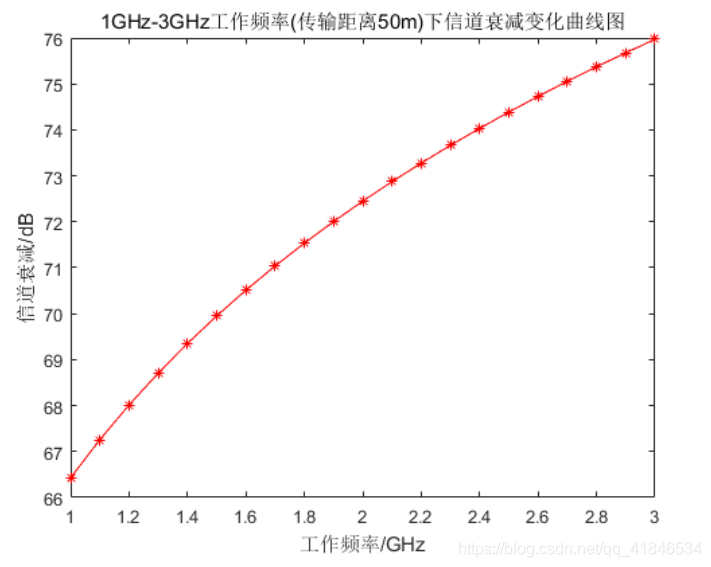
圖2-8 1GHz-3GHz工作頻率（傳輸距離50m）下通道衰減變化曲線圖

由圖可知，若只考慮直射波損耗，則在整個傳輸過程中，傳輸損耗的大小僅與傳輸距離、訊號工作頻率有關。訊號工作頻率一定（2GHz），傳輸距離在15m以下增加時，通道衰減變化較大，而在15m後衰減增長逐漸趨於穩定。而在傳輸距離一定（50m），工作頻率在1GHz—3GHz間變化時，通道衰減與工作頻率的關係更趨向於線性。當工作頻率一定時，傳輸距離在5m—100m變化過程中，通道衰減較大，整體衰減接近30dB；而當傳輸距離一定時，工作頻率在1GHz—3GHz變化過程中，通道衰減較小，接近10dB，其主要原因在於直射波損耗中上述兩個引數的變化帶來的影響。

三、總結

本文主要探究了數位通訊系統簡易通道編碼原理，包括重複編碼、交織編碼、擴頻調變解調、BPSK 調變解調等技術。從公式推導和模擬分析角度，梳理了收發機針對通道編碼的大體流程並對流程中應用的編碼技術進行效能分析。
而整個設計的過程和思路從一定角度上而言較為簡易卻又繁瑣，需要經過更深層次的學習來進一步改善，在運用更加先進的編碼技術提升訊號處理靈活性的同時，降低系統運算的複雜度。

注：本文為原創文章，其中存在些許個人主觀理解，希望讀者對其中相關知識有所取捨，也歡迎質疑討論。