ccf 1246 最詳細的菜鳥解析

ccf 1246

一百分的程式碼咱就不奢望了，送上九十六分程式碼，供大家參考參考。
題目連結：http://118.190.20.162/view.page?gpid=T102

觀察測試點知道，大多測試點的s都只有一位或者兩位。最後一個測試點，贊就直接放棄了。
觀察測試點和字串長度可以知道，當n足夠大的時候，字串長度會變得巨大，暴力方法肯定不行。所以需要一定的規律。

觀察得知，在字串中，s為一位或兩位的情況只有14種。
一位：1，2，4，6
兩位：16，26，41，42，44，46，61，62，64，66

再觀察字串，可以得到一個這樣的關係圖：（懶得畫了，直接用了另一個博主的圖，連結：https://www.pythonheidong.com/blog/article/433221/）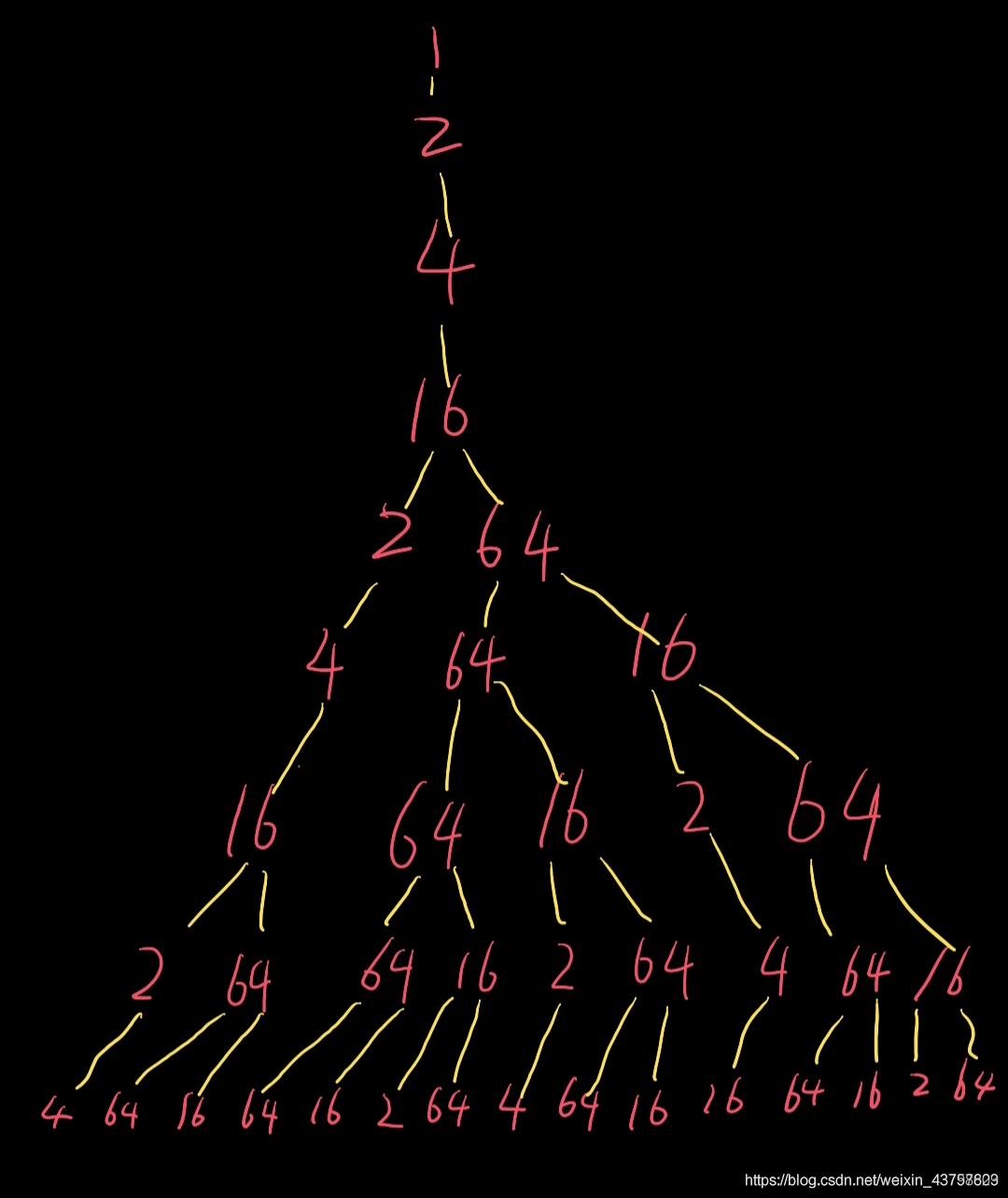
通過這樣的一個關係圖，我們能得到上一個串和下一個串的遞推關係。思路雛形就出來了，利用動態規劃應該可以解決這個問題。
兩位數分叉原理：比如16，就分為2的一次方和2的六次方。

通過這個圖我們可以知道：
下一個串的2可以由上一個串的1得到
下一個串的4可以由上一個串的2得到
下一個串的1和6可以由上一個串的4得到
依此類推，我們就可以得到s為一位的情況下的遞推關係。

接下里就是難點一，如何得到s是兩位的情況下的遞推關係。
其實我們把上面的圖變通一下，把本來不相鄰的組合起來，發現也可以得到同樣的效果。
例如：16可以產生264，劃分成（26）4，既可以得到26.
這裡需要解決的思想難題是，為什麼264只計一個26，為什麼不計其他的組合方式呢。
因為其他組合方式在s為一位的時候就已經被計數了，再計的話，就會出現重複，而26是由兩個不同的兩個陣列合而來，在s為一位時不會被計數。

理解了上面的思想，我們就能得到對照表1：

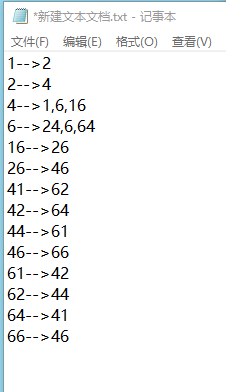
其表達的意義是：上一個串中的1的數量等於下一個串中2的數量。即上一個串中的1通過上訴關係變成了下一個串中的2.
理解了對照表，我們就需要從對照表中提取遞推關係。並進行編號處理，得到遞推關係表。

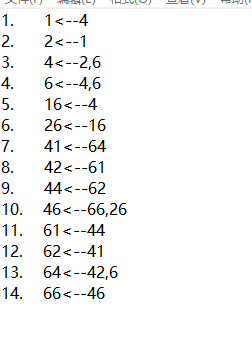
通過對照表，我們可以得到如下的遞推表，然後對遞推表進行編號。
上圖遞推表告訴我們：
下一個串中的1是由上一個串中的4得到的。
下一個串中的4是由上一個串中的4，6得到的。

通過遞推表和數位編號，得到遞推關係：
類似：
f(i)(1)=f(i-1)(3)
f(i)(2)=f(i-1)(1)
f(i)(3)=f(i-1)(2)+f(i-1)(4)
f(i)(4)=f(i-1)(3)+f(i-1)(4)
…

到這裡，串中各個數位的遞推關係就得到了，如何處理遞推變成了當前面臨的問題。

先舉一個簡單例子，斐波那契數列，就是個十分經典的遞推關係。
f(n)=f(n-1)+f(n-2)
如果把【f(n-1)，f(n-2)】看作是一個向量，那這個向量乘以矩陣【【1，1】【1，0】】則可以得到新的向量【f(n)，f(n-1)】.。
這就是利用矩陣來推進遞推關係。也就是，把遞推的上一個狀態，乘以一個矩陣，得到遞推的下一個狀態。這個思想就是破題關鍵點之一。

然後我們理解一下破題的下一個關鍵點。就是快速冪。要求2^16，我們也許回想，把16個2相乘。這樣固然能得到結果，但是當次方數足夠大時，這樣的計算方式就十分拉跨。於是我們引入快速冪。
當前兩個2相乘時，我們就把原題變成了4^8。重複這樣的操作，就可以減少大量的運算。當冪變了奇數時，就單獨拿一個冪出來，再將剩下的偶數冪繼續進行快速冪運算，最後把拿出來的奇數冪乘回去。

瞭解了矩陣遞推思想和快速冪思想，結合上訴的遞推關係式，就可以進行計算了。
當然，難點在於遞推關係到矩陣的轉換過程，這個過程沒辦法幫忙，需要自己理解。

這就是14為遞推關係對應的dp矩陣。注意，這個dp矩陣的向量方向時縱向的。）

初始結果集：

利用矩陣乘法的結合新，我們可以用快速冪的方法，求出所有矩陣的乘積，再把算出的矩陣乘進結果集，直接得結果。如果中間有奇數冪出現，就取出奇數冪先乘進結果集中，剩下的偶數冪繼續進行快速冪運算。

當然，直接進行14位元的矩陣遞推可能不好理解，可以用

四位的矩陣和四位的結果集來進行遞推理解，再拓展到14位元上。

上程式碼：

import java.util.Scanner;
import java.util.Map;
import java.util.HashMap;;

//快速冪+dp遞推矩陣
class Matrix{	
	public long[][] Ma_Ma(long [][] dp){//類似這種值很大的題目，尤其需要關注結果範圍和考慮溢位。
		int n=dp.length;
		long [][] temp=new long[n][n];
		//兩個相同的矩陣相乘，dp遞推矩陣相乘
		for(int i=0;i<n;i++) {
			for(int j=0;j<n;j++) {
				for(int k=0;k<n;k++) {
					temp[i][j]+=(dp[i][k]*dp[k][j]);
					temp[i][j]%=998244353;//結果太大，如果不進行取餘操作，會結果溢位，出現負值
				}
			}
		}
		return temp;
	}
	
	public long[] Ma_Ve(long [][] dp,long []res) {
		int n=dp[0].length;//矩陣的列數
		int m=res.length;
		long [] temp=new long[m];
		//結果向量與矩陣相乘
		for(int i=0;i<n;i++) {
			for(int j=0;j<m;j++) {
				temp[i]+=(res[j]*dp[i][j]);
				temp[i]%=998244353;//結果太大，如果不進行取餘操作，會結果溢位，出現負值
			}
		}
		return temp;
	}
}

public class DP {
	public static void main(String[] args) {
		//初始的結果向量（n=0）時。
		long [] res =new long[14];
		res[0]=1;
		//dp矩陣,矩陣向量方向是行方向，第一次因為乘了列方向的向量，導致錯誤。
		long [][] dp= 
			{{0,0,1,0,0,0,0,0,0,0,0,0,0,0},
			{1,0,0,0,0,0,0,0,0,0,0,0,0,0},
			{0,1,0,1,0,0,0,0,0,0,0,0,0,0},
			{0,0,1,1,0,0,0,0,0,0,0,0,0,0},
			{0,0,1,0,0,0,0,0,0,0,0,0,0,0},
			{0,0,0,0,1,0,0,0,0,0,0,0,0,0},
			{0,0,0,0,0,0,0,0,0,0,0,0,1,0},
			{0,0,0,0,0,0,0,0,0,0,1,0,0,0},
			{0,0,0,0,0,0,0,0,0,0,0,1,0,0},
			{0,0,0,0,0,1,0,0,0,0,0,0,0,1},
			{0,0,0,0,0,0,0,0,1,0,0,0,0,0},
			{0,0,0,0,0,0,1,0,0,0,0,0,0,0},
			{0,0,0,1,0,0,0,1,0,0,0,0,0,0},
			{0,0,0,0,0,0,0,0,0,1,0,0,0,0}
			};
		//對照表
		Map<Integer,Integer> map=new HashMap<Integer,Integer>();
		map.put(1,0);
		map.put(2,1);
		map.put(4,2);
		map.put(6,3);
		map.put(16,4);
		map.put(26,5);
		map.put(41,6);
		map.put(42,7);
		map.put(44,8);
		map.put(46,9);
		map.put(61,10);
		map.put(62,11);
		map.put(64,12);
		map.put(66,13);
		
		Scanner in=new Scanner(System.in);
		int n=in.nextInt();
		int s=in.nextInt();
		in.close();
		
		Matrix ma=new Matrix();
		//快速冪核心程式碼
		//利用矩陣乘法的交換性和結和性。先算後面所有矩陣的矩陣乘法，把最後得到的矩陣乘入結果向量，得到最終結果。
		//快速冪思想，就是利用上一次的計算結果作為新的基數，使得計算技術指數式減少。
		//當遇見冪數為奇數時，就先取出一個乘進結果集，剩下的偶數冪再進行快速冪運算
		while(n>0) {
			if(n%2==1) {
				res=ma.Ma_Ve(dp, res);
			}
			dp=ma.Ma_Ma(dp);
			n>>=1;//移位運算
		}
		
		System.out.print(res[map.get(s)]);
		
	}
}