二進位制炸彈的拆除——張渣渣_的學習記錄（1）

張渣渣_的學習記錄（1）之二進位制炸彈的拆除

二進位制炸彈闖關
我們學校計算機系統基礎課程的大作業，現在我把自己做實驗的整個過程貼在下面，希望大家對不足的地方加以指正。
（因為自己在學習的過程中還是有很多的不足，所以在之後的部落格中，我會有一篇專門對這篇文章中不足的地方進行補充。

話不多說，我們直接開始！！！！！！

【大作業要求】
該大作業為闖關實驗，共需破解7關。下載壓縮檔案，在Debian系統裡進行解壓縮，通過對可執行檔案bomb反組合，分析組合程式碼並獲取相關線索，從而破解每一關的輸入內容，完成闖關。

【闖關結果】
1、闖關情況

2、破解執行結果
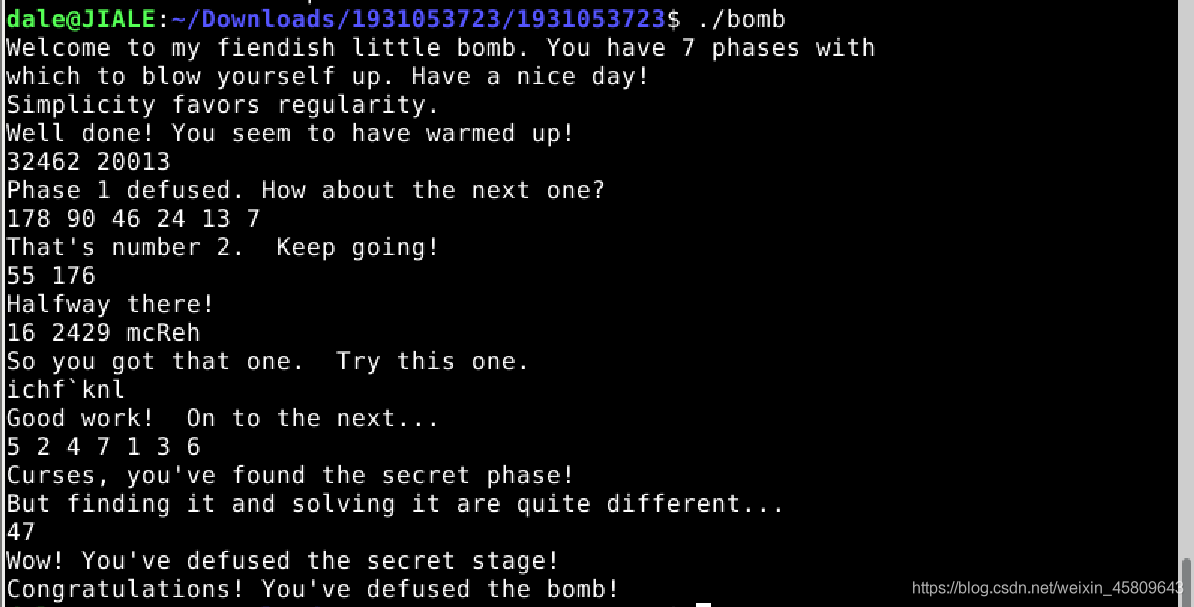圖1 破解執行結果

【程式碼分析】
對成功破解階段的程式碼給出分析說明。

階段0
phase_0
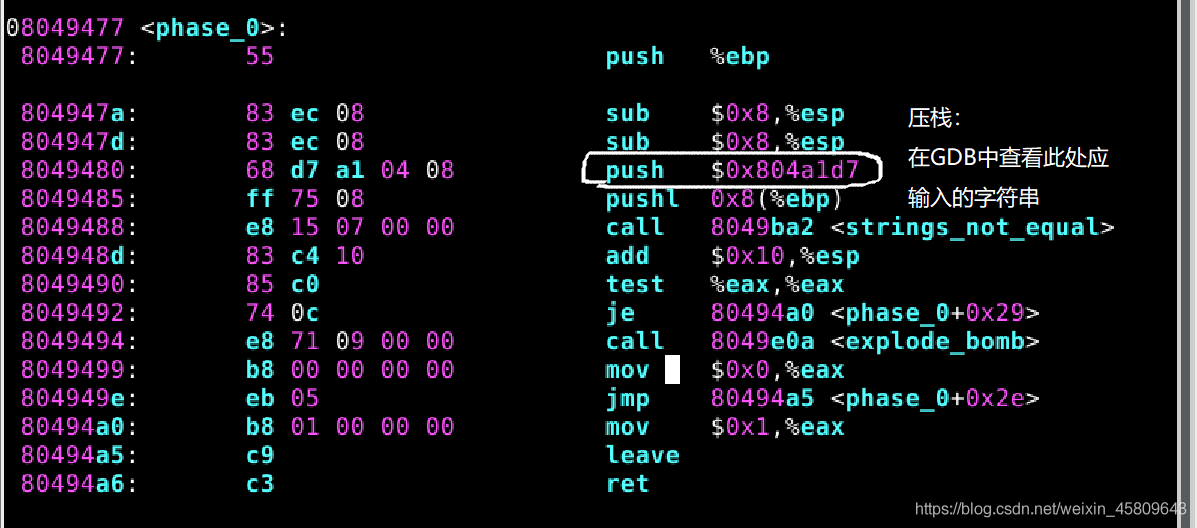圖2 phase_0原始碼及分析

使用objdump生成bomb程式的組合程式碼，下圖將組合程式碼定位在給出了第一關字串對比的地方<phase_0>。可以看出在呼叫<string_not_equal>函數前，現將要參與對比的兩個字串壓入棧中，push $0x804a1d7就是存放內建字串的首地址，pushl 0x8(%ebp)是使用者輸入字串的首地址。
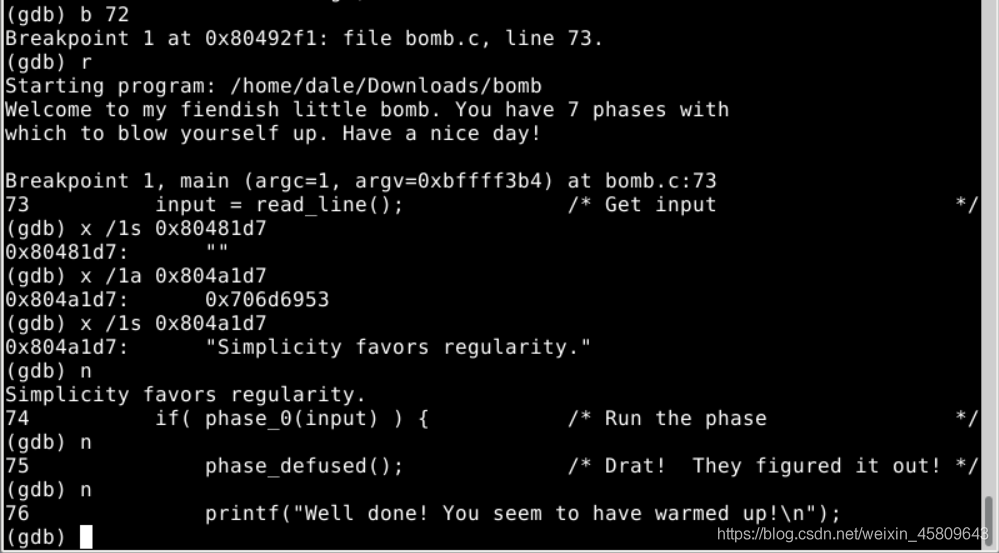圖3 phase_0 gdb偵錯

gdb進行偵錯，斷點設定在b 72。這時根據組合語句中發現的內建字串首地址0x804a1d7，使用examine指令顯示這個字串為」Simplicity favors regularity.」。

圖4 phase_0通過
單步或繼續執行後續的程式碼時輸入這個字串，結果顯示成功過關。
第零關（phase_0)已破解！！！

階段1
phase_1
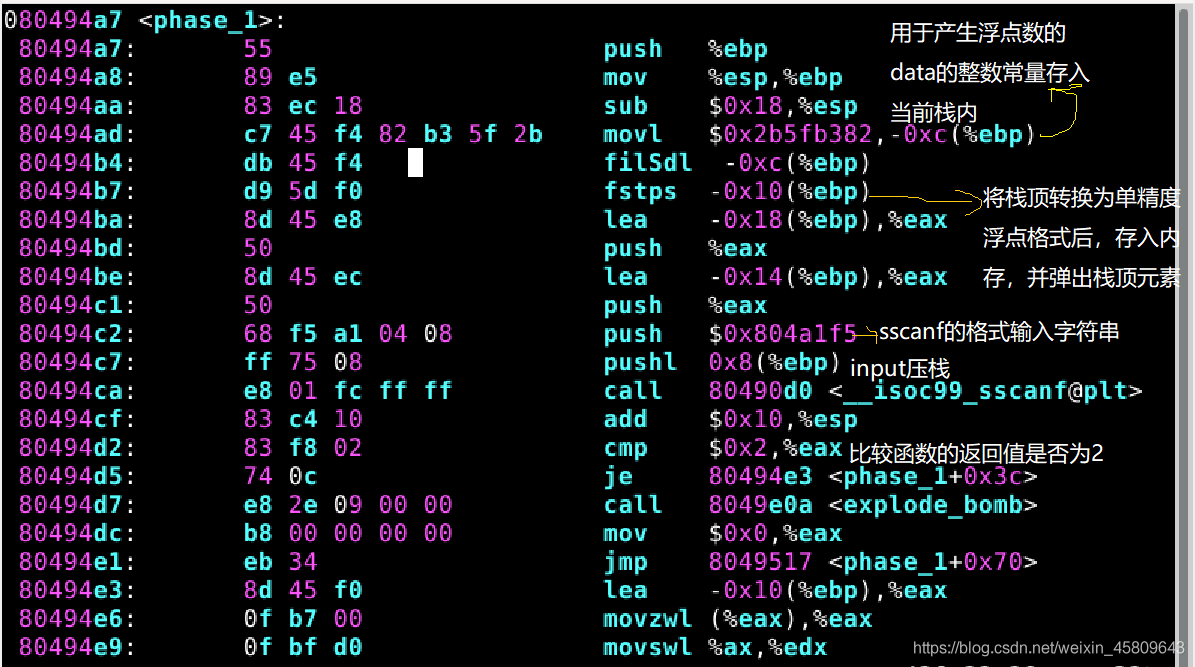圖5 phase_1原始碼及分析

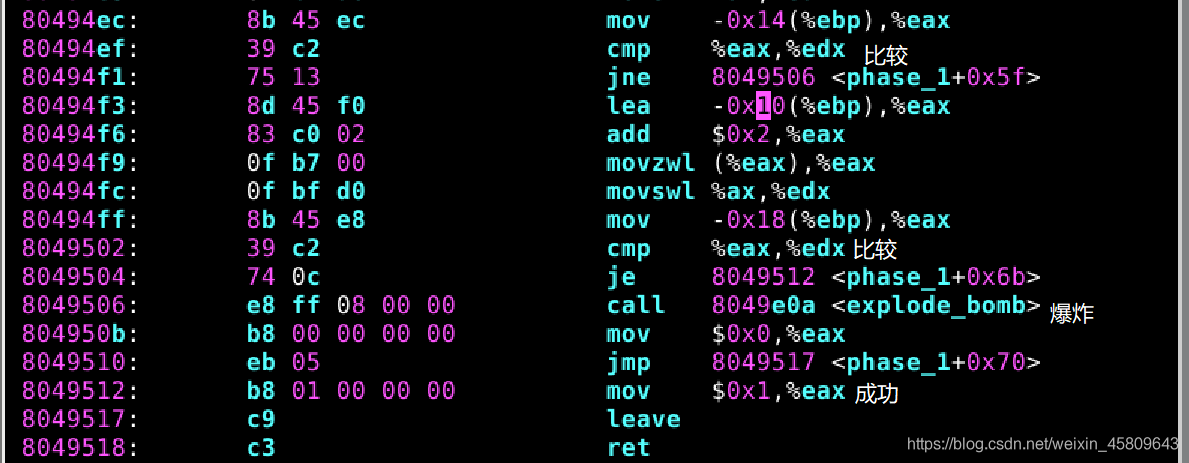圖6 phase_1原始碼及分析

先使用gdb檢視第二關所需要輸入的型別：
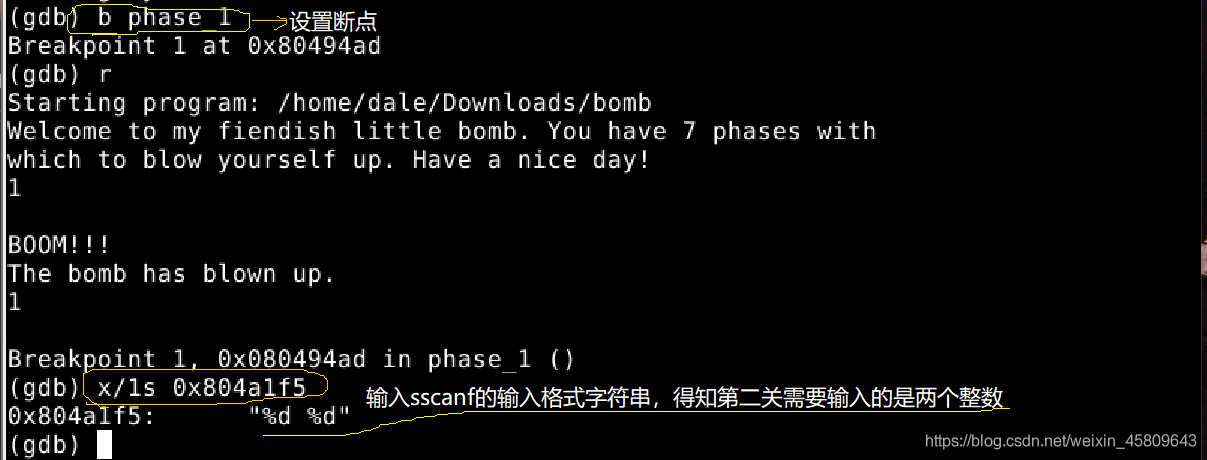圖7 phase_1gdb檢視輸入格式

由gdb偵錯得知，在第二關需要輸入的是兩個整數。由於計算浮點數時出現計算問題，所以，在這一關採用檢視暫存器內容的方法來解決。
此次需要使用的指令分別是：si;finish;disas;info registers
兩次檢視地址分別為0x080494f1和0x08049504

整個的過程如下：
先設定斷點，然後在斷點之前是要進行輸入第零關和第一關的結果，因為兩關之間無關聯，所以節省時間第零關隨便輸入即可，到了第一關要根據gdb得到的格式輸入。
第二步，再用si進行跳轉，當出現80494ca這一行的呼叫函數語句的時候，用finifh指令。
第三步，呼叫完finish之後，先用空格使得整個的程式碼能完整的呈現出來，然後在左側你可以通過一個小箭頭看到當前程式碼執行的地方，觀察整個的程式碼，找到兩次比較出現的地址。
第四步，用si進行跳轉，到第一次比較的地方的時候用info registers進行第一次檢視。
第五步，檢視到第一個數位之後，退出這一輪，重新進行第二次檢視的過程。（往下翻，兩張圖之後有注意的點，一定要耐心看）
第六步，得到兩個數位，進行驗證。

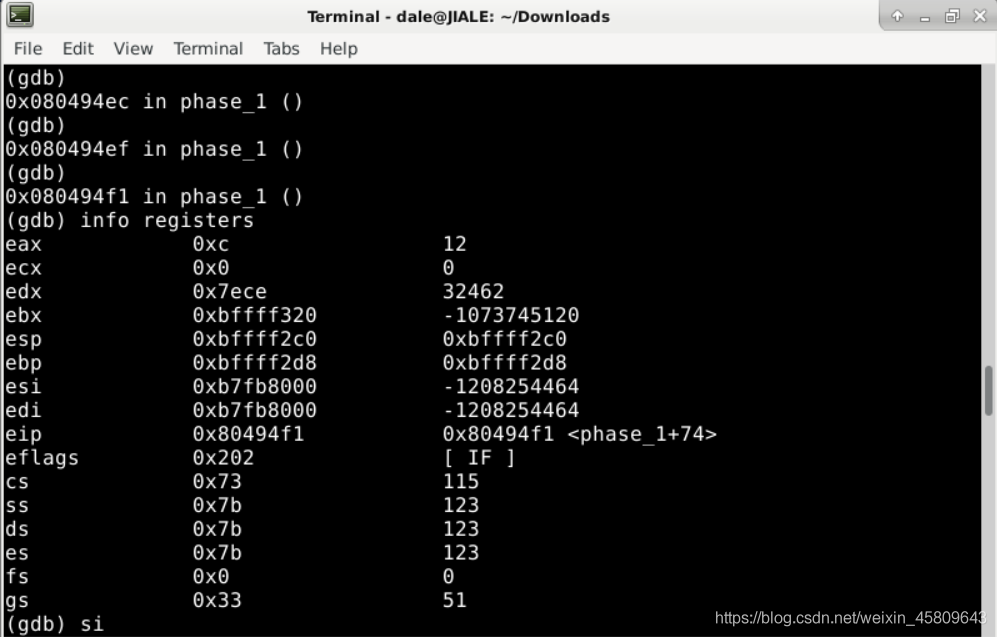圖8 檢視暫存器內容得到第二關的通關碼

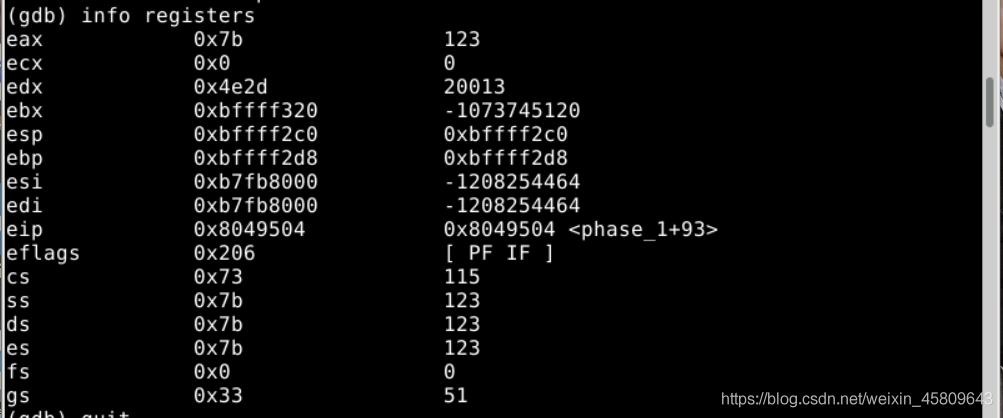圖9 檢視暫存器內容得到第二關的通關碼

這裡非常需要注意的點是（雖然有點繞，但是我相信挑戰拆彈實驗的你一定能看懂）：

要耐心哦！

當通過gdb得到了輸入格式之後（以我自己的為例），在第一次的檢視暫存器的內容的時候，需要輸入的是兩個任意的整數，這樣就可以通過info registers檢視我所需要輸入的第一個數位，在第一個數位得到之後，要做的結束此次檢視的過程，重新進入第二次檢視暫存器的內容，前面設定斷點等操作都一樣，不同的是，當輸入兩個數位的時候，就必須先輸入我剛得到的正確的數位，第二個數位就可以寫一個任意的整數，然後用si進行跳轉，用info registers語句檢視。

（這樣操作的原因是，第一個數位輸入正確與否，之後的語句跳轉都依賴它，如果第一個數位輸入錯誤，那麼接下來就會跳轉到炸彈爆炸的語句，第一次檢視暫存器的時候，我任意輸入了兩個整數，當我得知了第一個正確的數之後，如果繼續，必然爆炸。）

驗證第二關答案，結果顯示已過關
圖10 phase_1通過

第一關（phase_1)已破解！！！

階段2
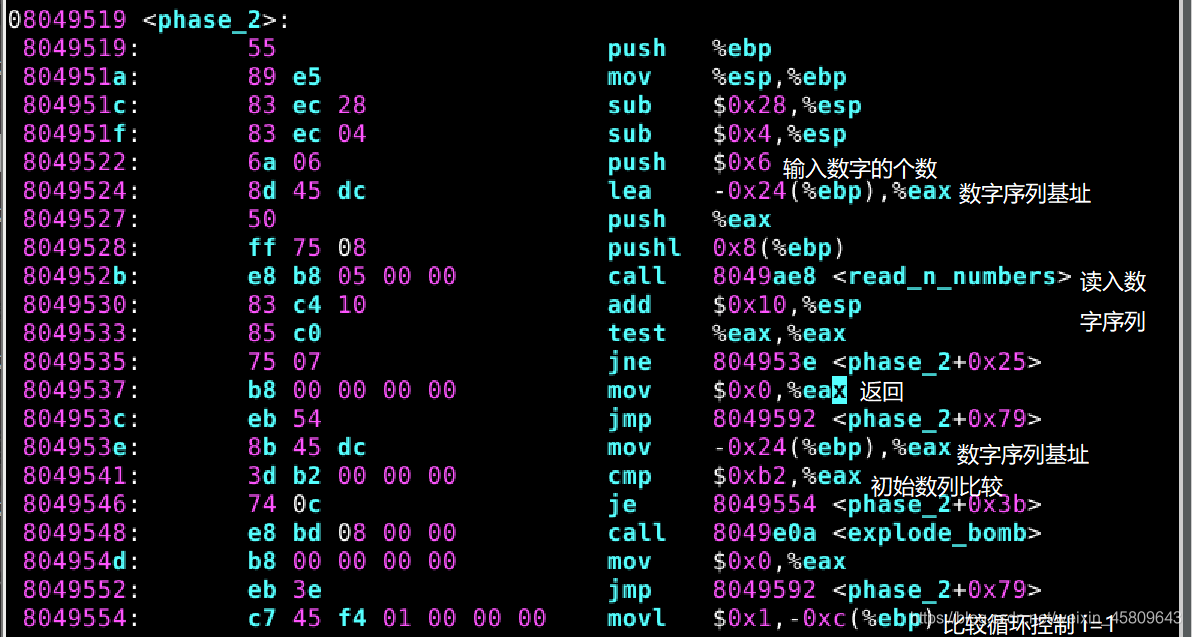圖11 phase_2原始碼及分析

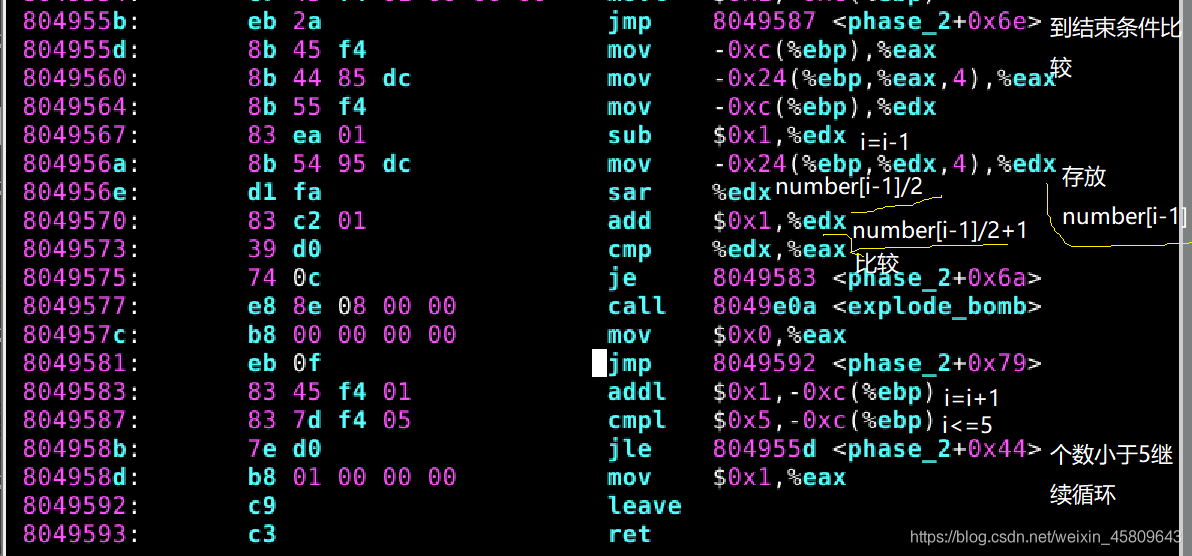圖12 phase_2原始碼及分析

注意注意注意哈！
這裡一定要先找到輸入數位是多少個，然後把迴圈條件找到，再進行運算就可以算出來了！
細節如下：
通過對原始碼的分析，找到了它的迴圈條件和迴圈體，對其進行運算：
number[i]=number[i-2]/2+1
又知，初始數位為0xb2=178 即number[0]=178。
number[1]=178/2+1=90;
number[2]=90/2+1=46;
number[3]=46/2+1=24;
number[4]=24/2+1=13;
number[5]=13/2+1=7。
驗證第三關所得答案，結果顯示已過關。
圖13 phase_2通過

第二關（phase_2)已破解！！！

階段3


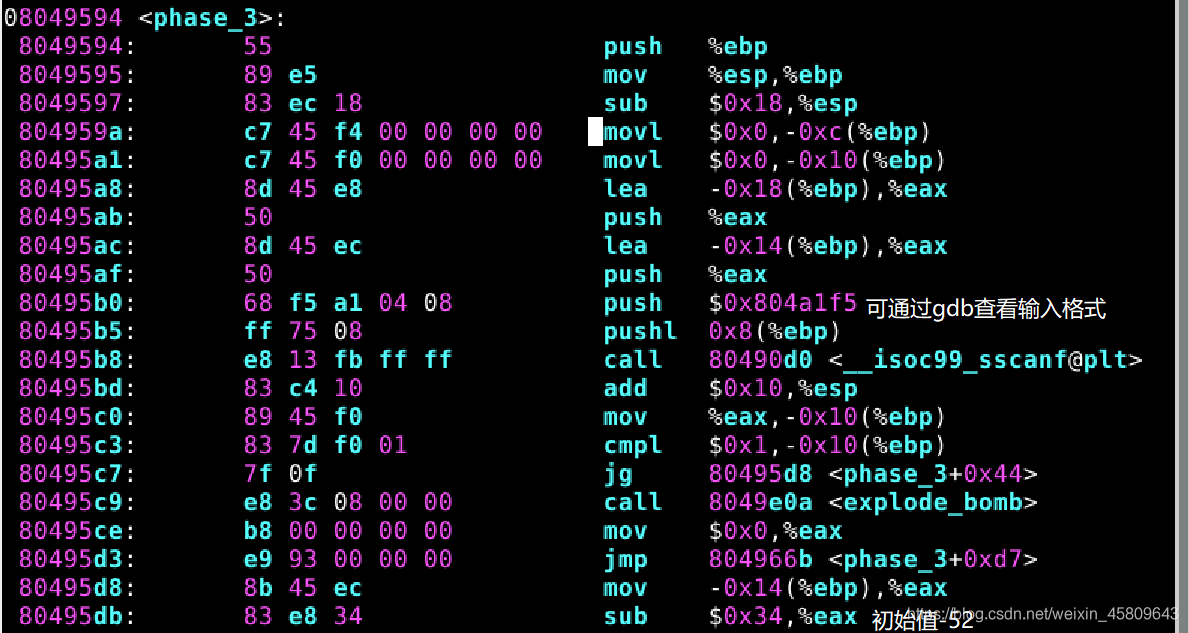
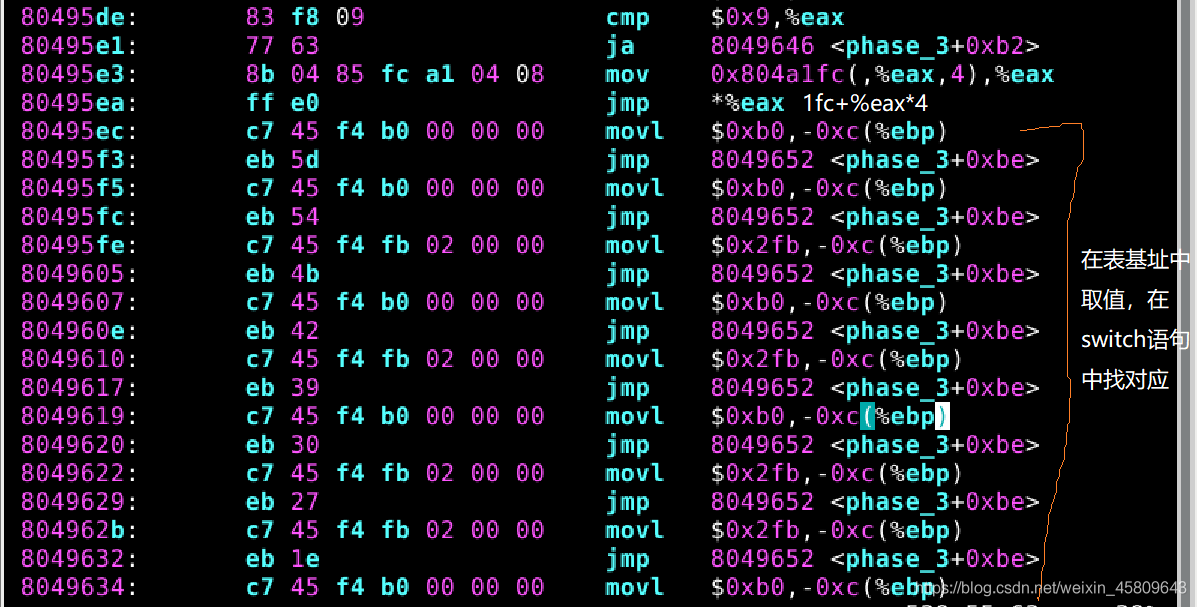
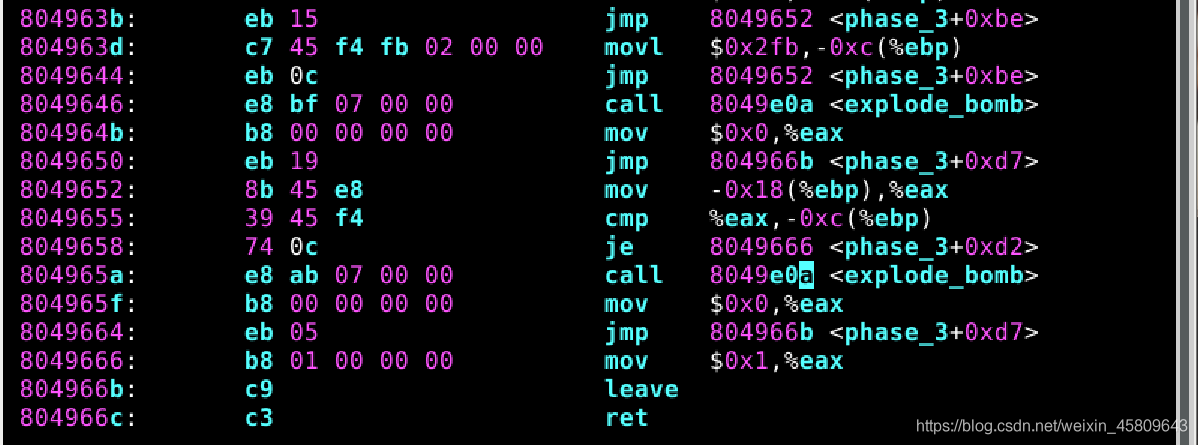圖14 15 16 phase_3原始碼及分析

在無法獲得源程式的情況下，只能通過對可執行程式進行反組合來獲得程式的組合程式碼。觀察bomb.s對應的組合程式碼，分析源程式的功能。
圖17 通過gdb檢視確定輸出兩個整數

這裡輸入格式也可能是「%d %c %d"（我朋友的就是）,但是都大同小異，只要初始條件和迴圈找得好，破解這一關就不難。

結合原始碼可以發現，程式內部對將要輸入的第一個數位的要求是減去52後的值小於9，第二個輸入數位應該根據第一個輸入的整數的值來判斷程式轉到哪個分支執行，從而確定第二個數位的值應該輸入哪個。
假設輸入值為55，然後通過計算在gdb中檢視表基址。
圖18 gdb檢視表基址

根據所找到的0x08049607在bomb.s中檢視跳轉，然後得到了對應的結果176，驗證成功。
（一定要看好自己的跳轉）
圖19 phase_3通過

第三關（phase_3)已破解！！！

階段4

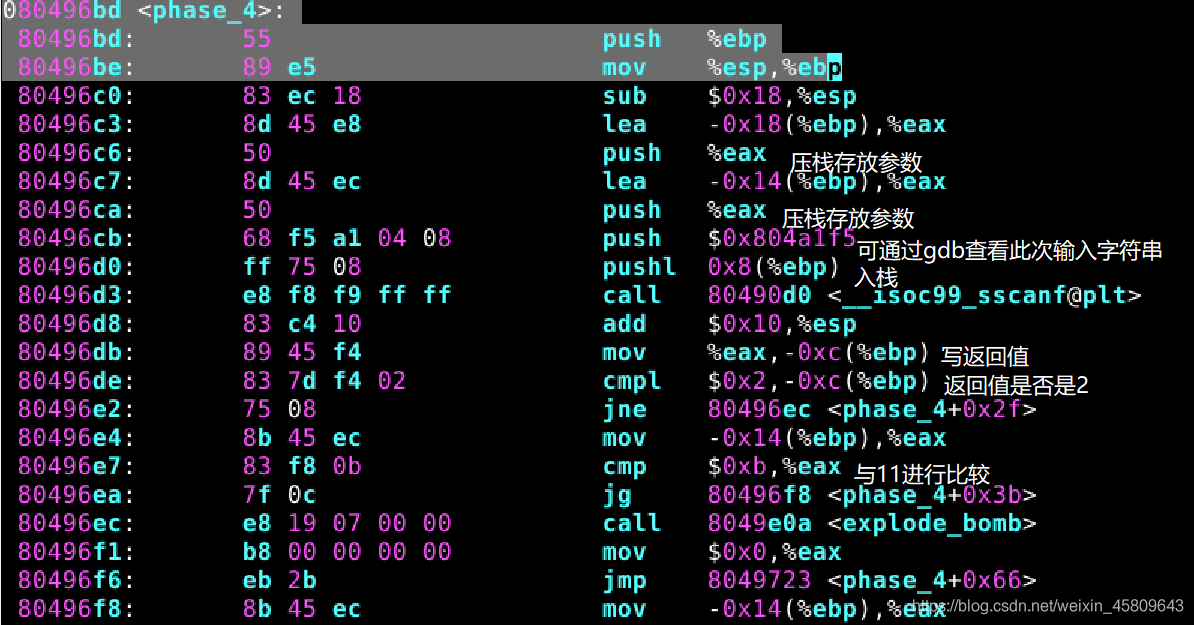
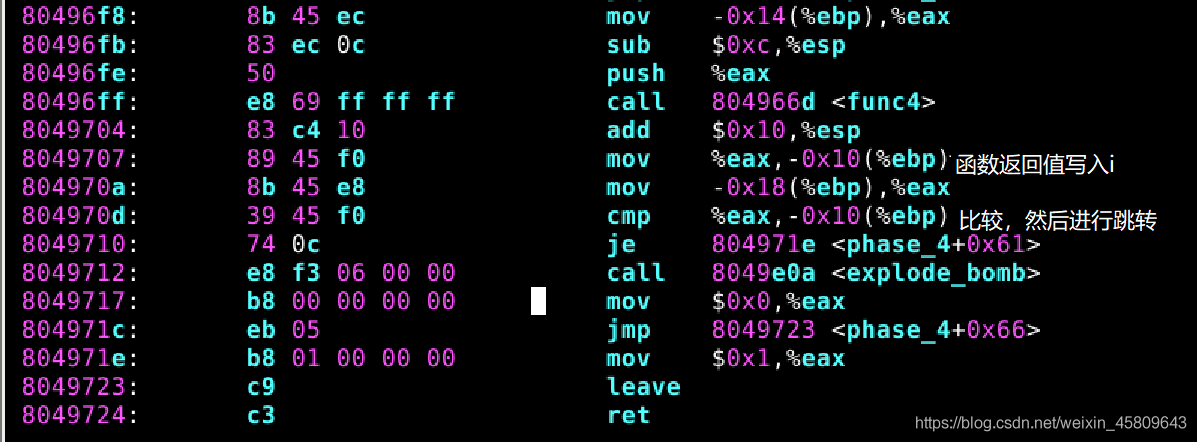
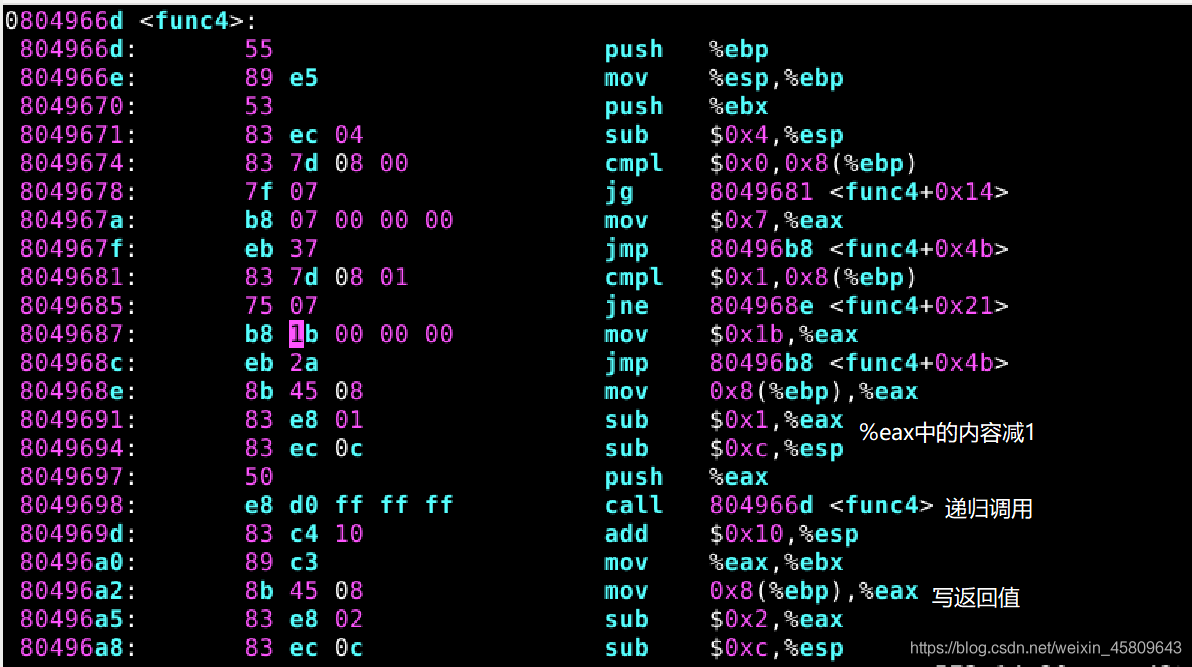
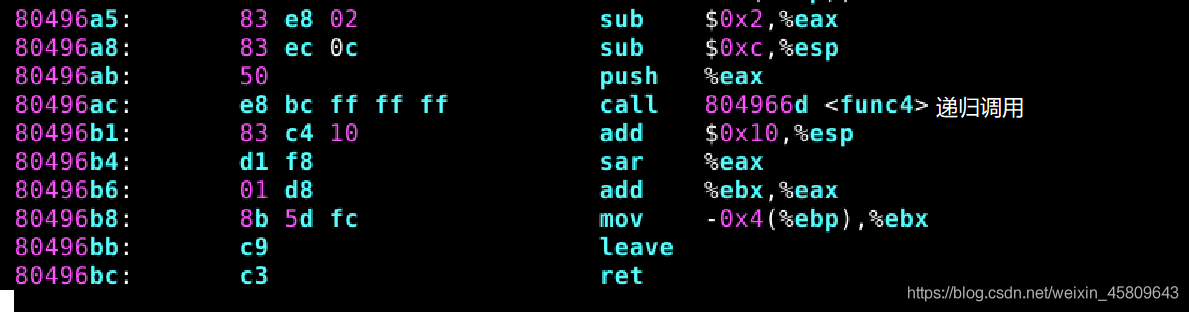圖20 21 22 23 phase_4和func4原始碼及分析

gdb進行偵錯確保推算的數位是正確的。

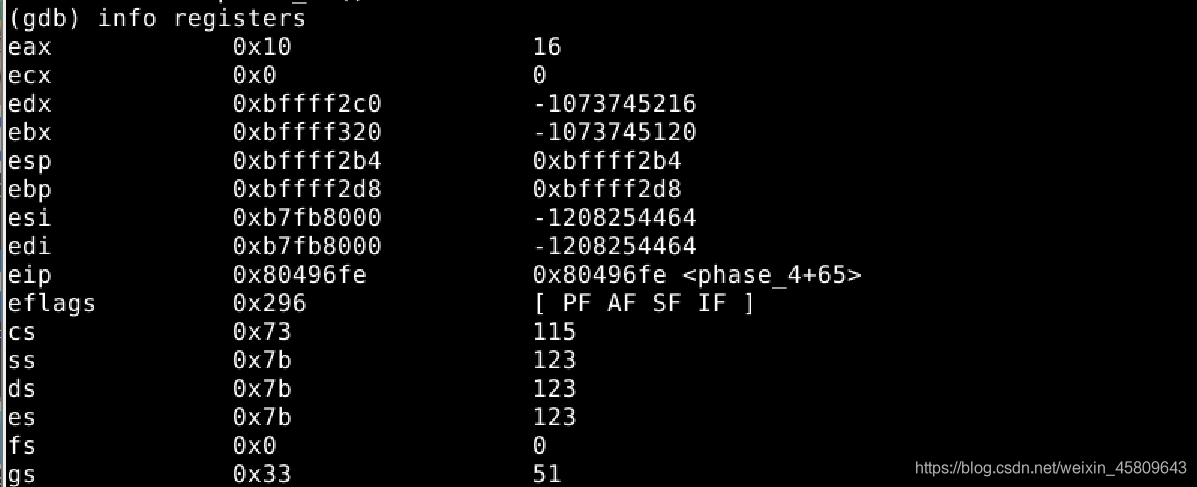
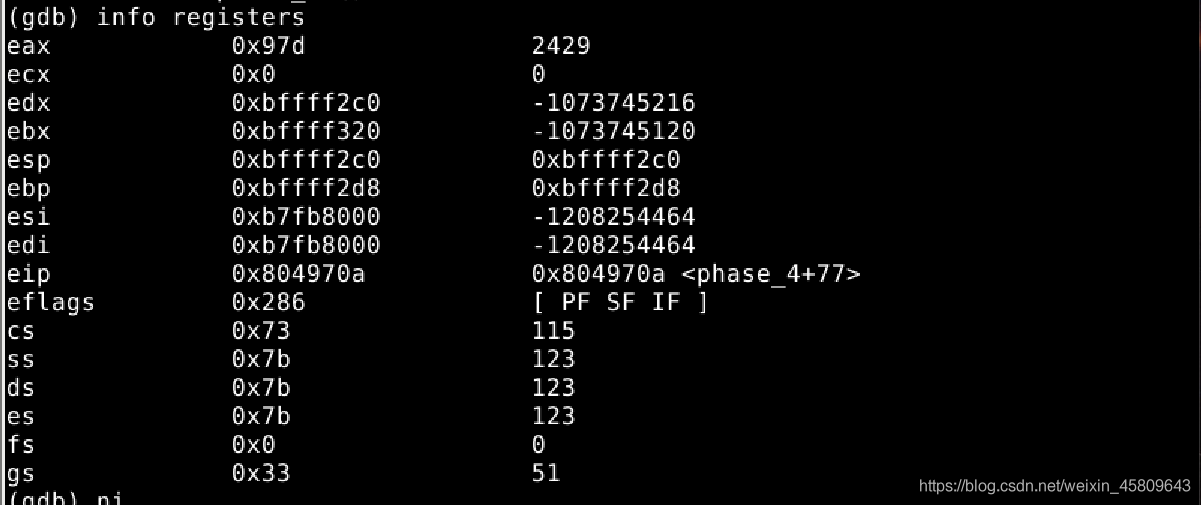圖24 25 驗證推算的數位的正確性
這裡其實我的方法更偏向於暴力拆解，整個過程類似於前文中的第一關，是檢視暫存器內容得到的。（這裡不足的地方我會通過之後的部落格進行補充，或者有朋友有其他方法也可私信我，我們一起討論呀！）

驗證第四關的結果：
圖26 第四關破解

第四關（phase_4)已破解！！！

階段5

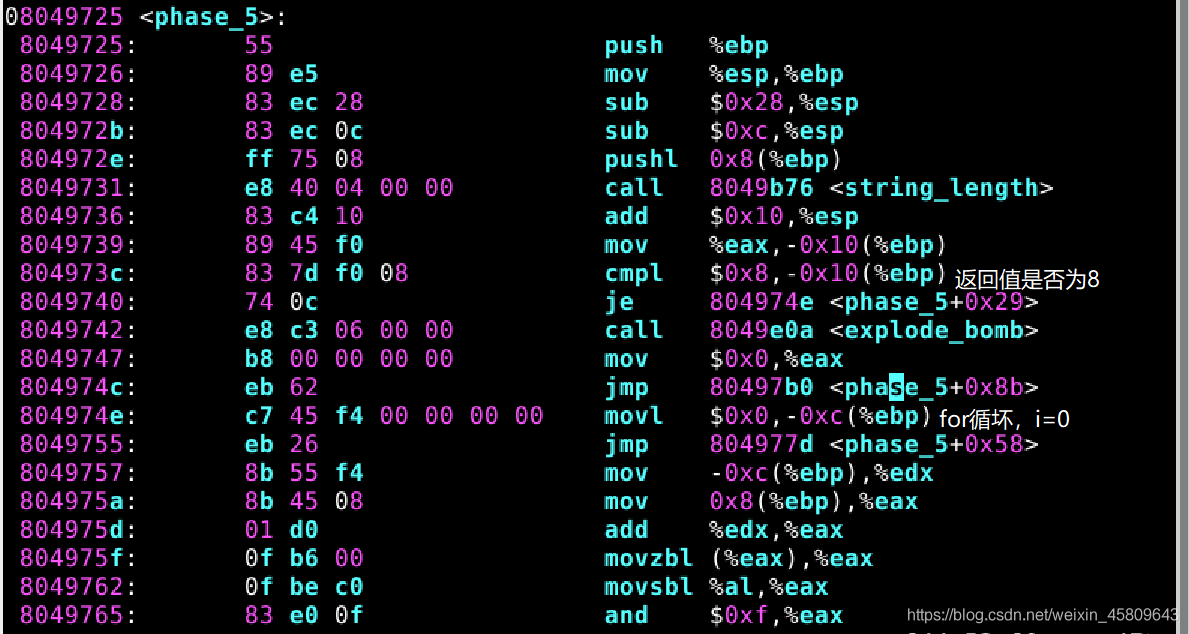
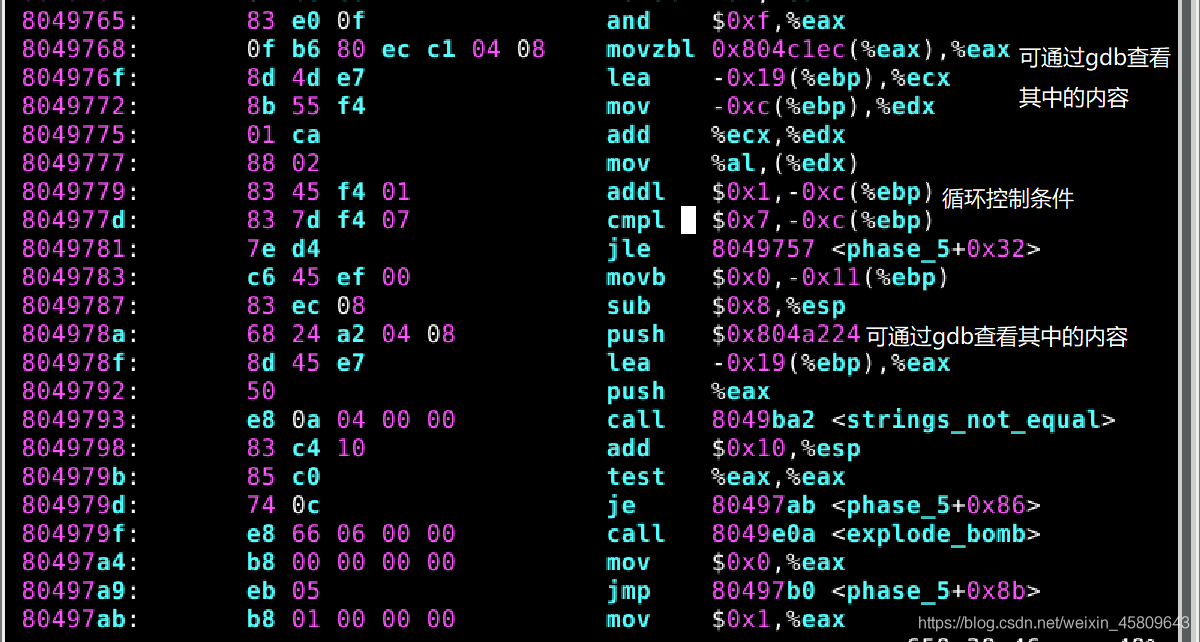圖27 28 phase_5原始碼及分析

這裡用到了一個迴圈，可能一開始會比較懵，所以我先利用gdb檢視了程式碼中明地址中到底存放了啥，於是就有了下圖：
圖29 第一個明地址中存放的內容

圖30 第二個明地址中存放的內容

乍一看，這都是啥，仔細一看，第二個明地址中有的字元第一個都有，這說明啥？
於是我想到了迴圈、指標、和索引！
應該就是根據迴圈，在一堆字元中找幾個字元的那種
然後又有了下圖
圖31 明地址找索引

由圖31得知，此關的通關密碼為ichf`knl
驗證結果正確：
圖32 phase_5通過

這裡其實我見到的更多的是給定一個數位，然後找出小於另一個數位的八九個數位之和是給定的這個數位，然後類似於我手寫的那種找索引，再看ASCII碼錶把數位翻譯出來就可以了。
第五關（phase_5)已破解！！！

階段6




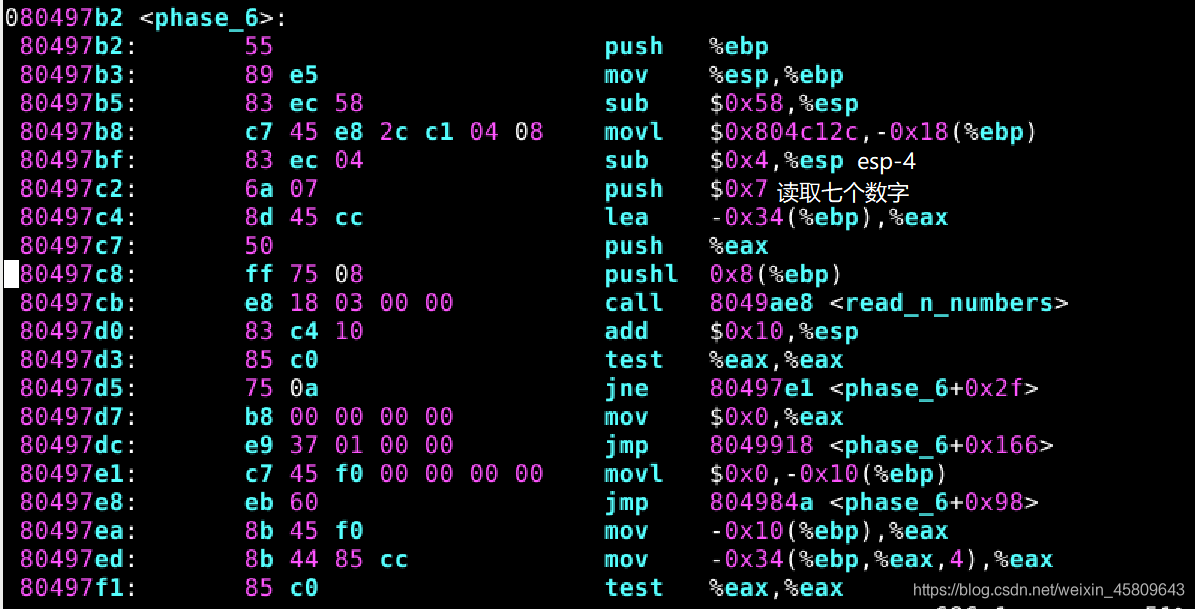
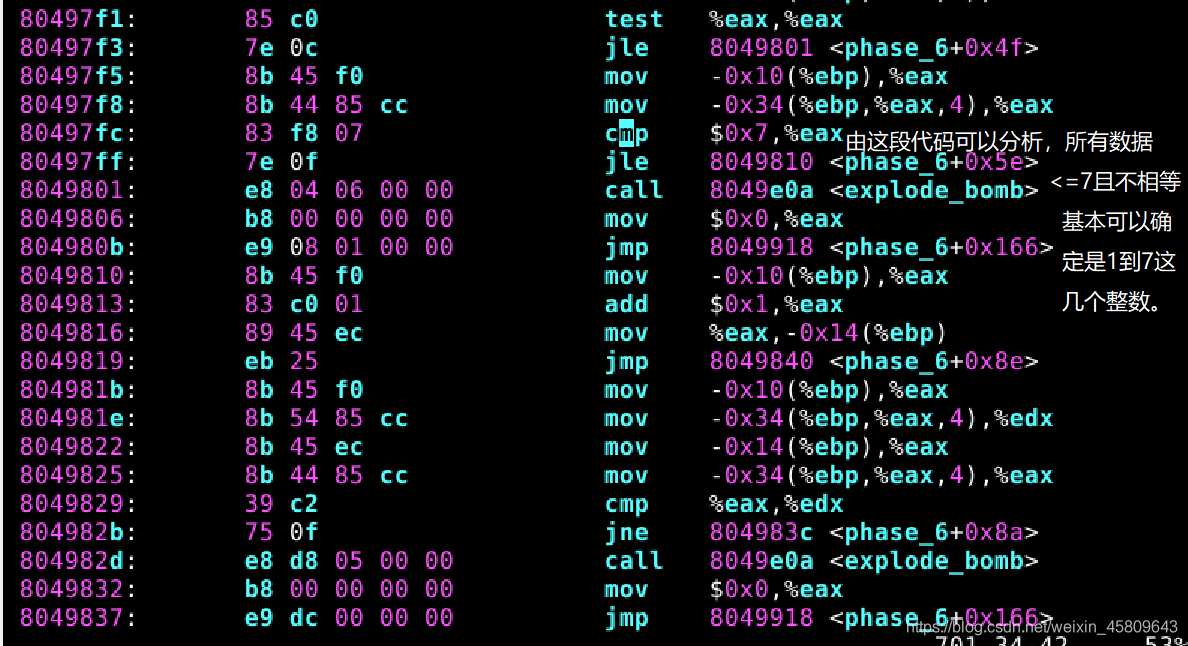
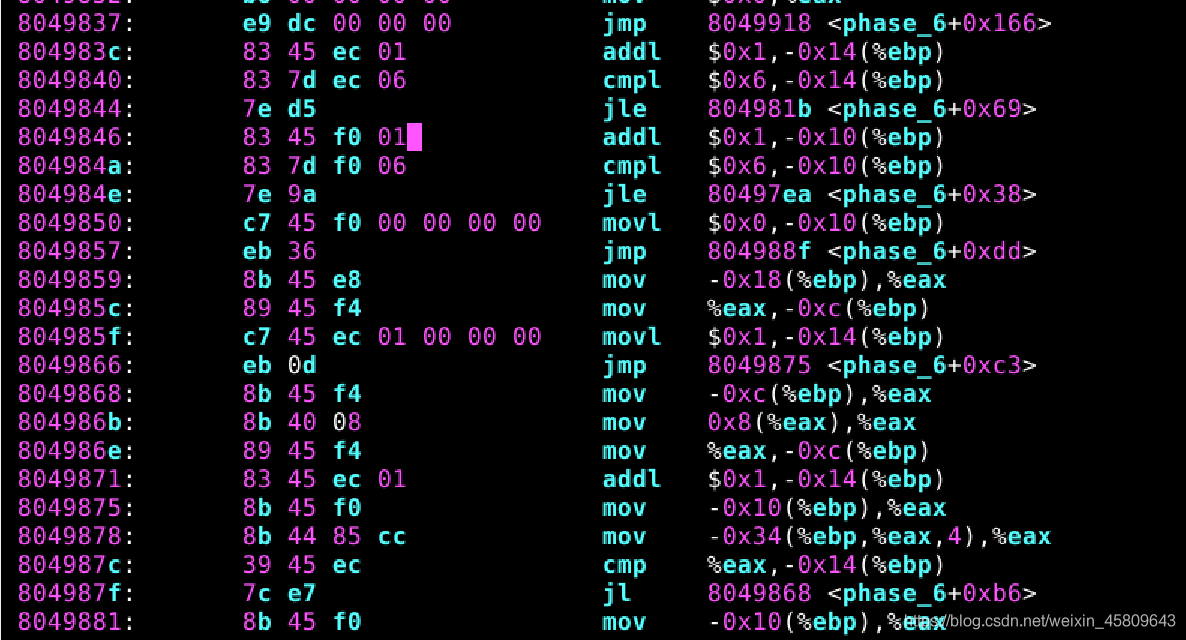
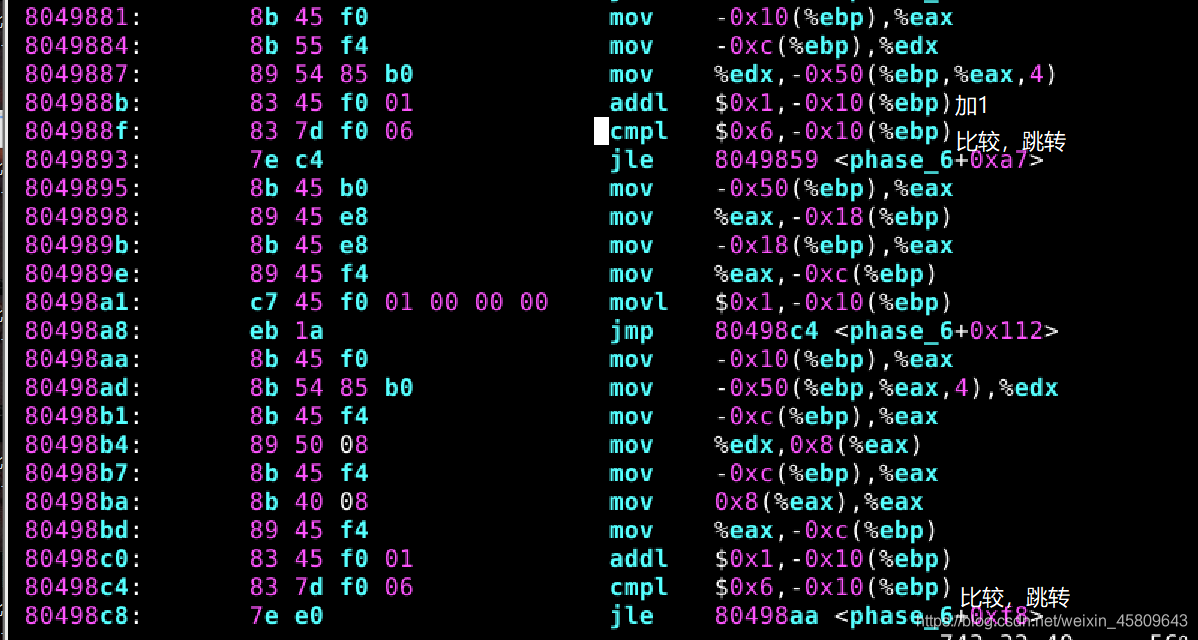
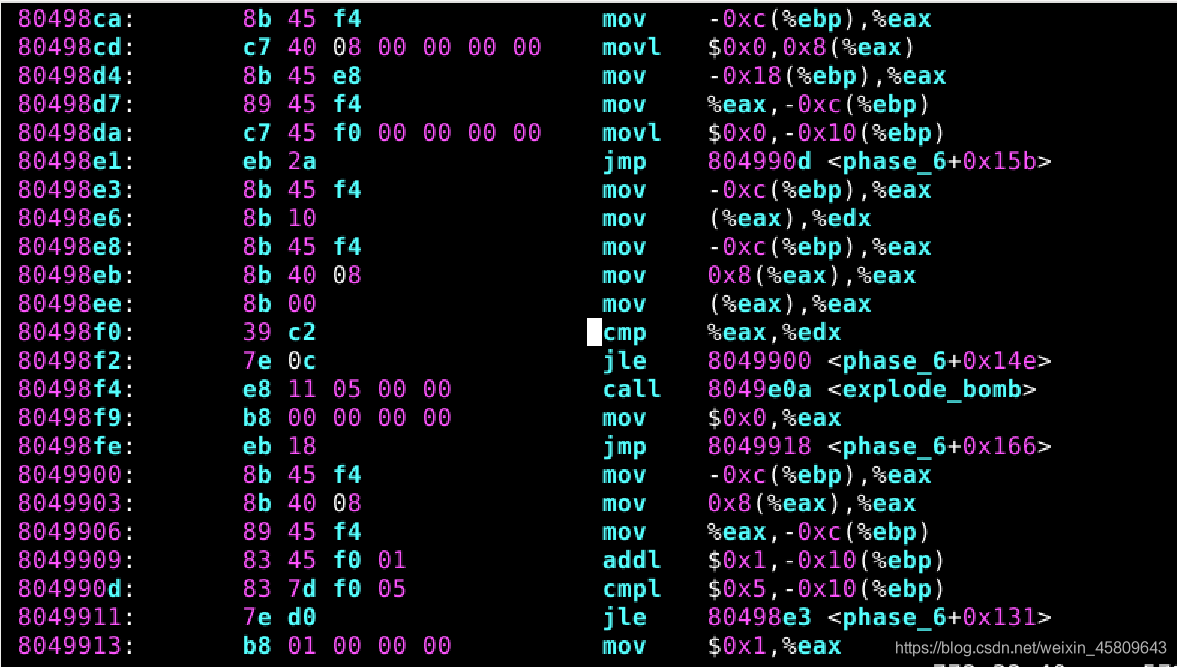圖33 34 35 36 37 phase_6原始碼及分析

在此關中，對原始碼進行分析，發現最終輸出的結果是按照升序排列數位然後輸出：
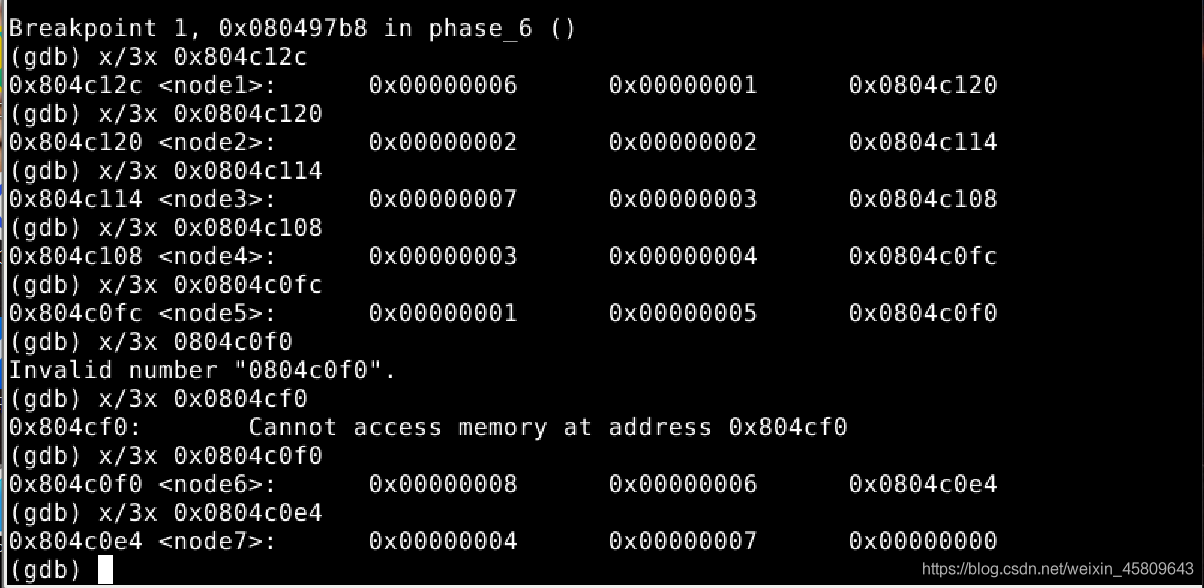圖38 設定斷點然後檢視

對所得數位進行驗證，得知最後得結果為5 2 4 7 1 3 6
圖39 phase_6通過
（這裡其實有一點小暴力拆解的意思，有興趣的朋友可以和我一起討論哈！）
第六關（phase_6)已破解！！！

階段7
這裡的階段七是對隱藏關進行破解的，剛開始我其實沒有發現這個，這個隱藏關是我朋友發現的。

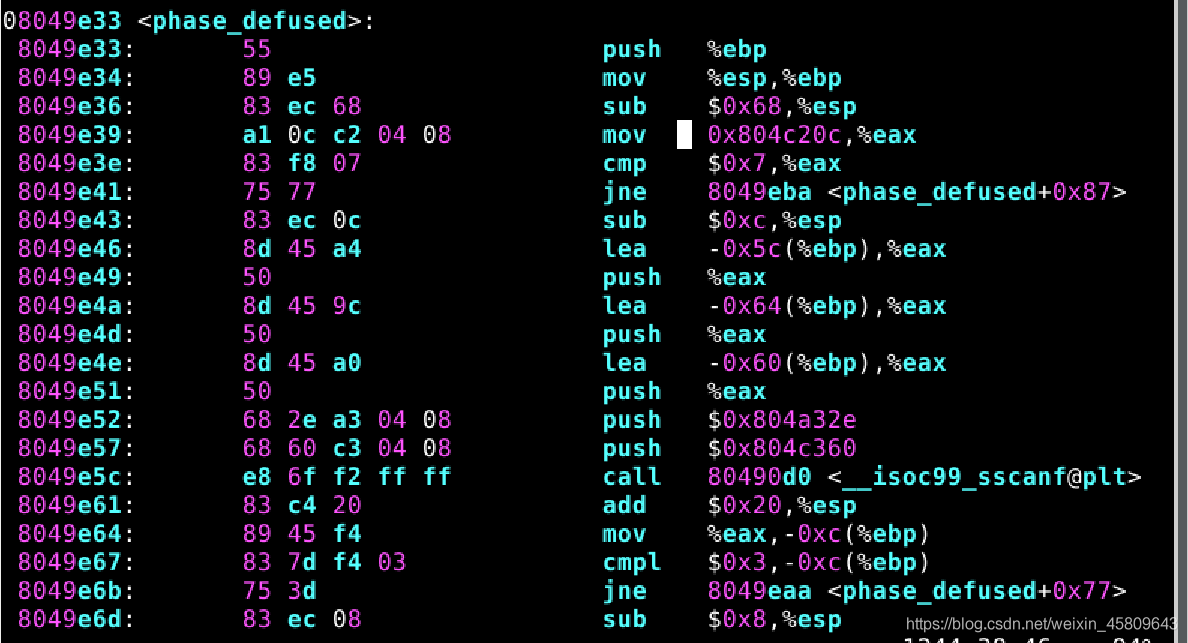
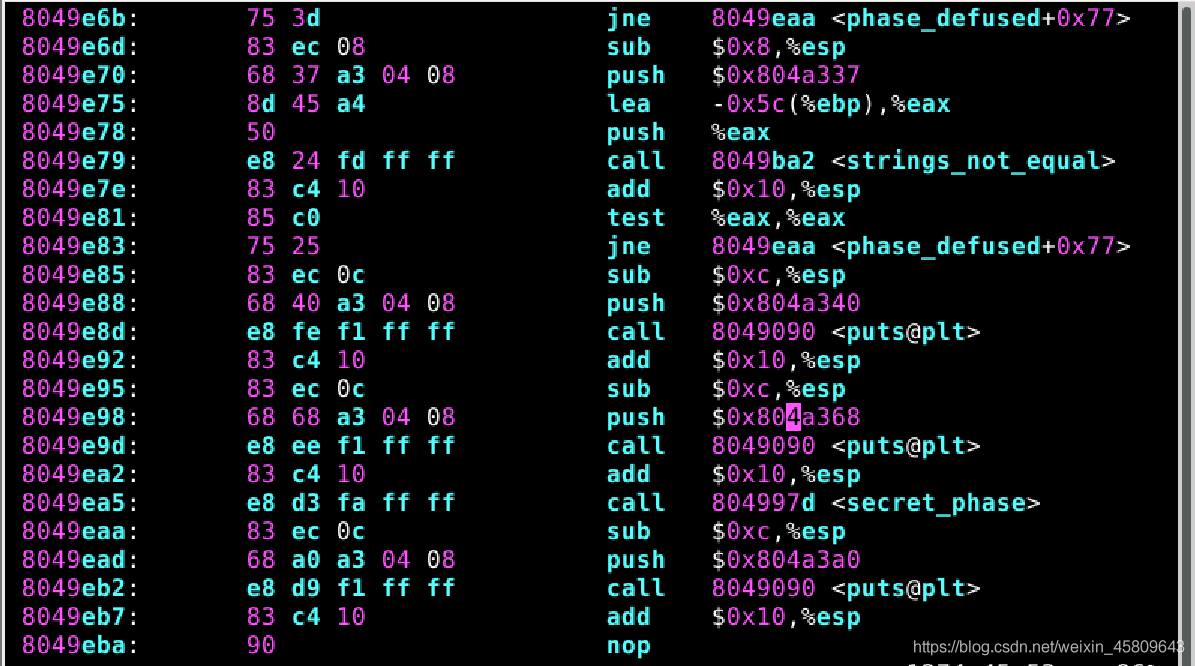圖40 41 隱藏關入口

對隱藏關中的組合進行分析，然後再通過gdb檢視明地址中得內容，最終可得知隱藏關的入口在phase_4,密碼為mcReh
圖42 隱藏關密碼及其格式

在這裡包含了一個小點，隱藏關的密碼是緊跟在兩個整數之後的，結合之前的破解以及分析（我徒手使試出來的），第一種情況如果將隱藏關密碼同時加在phase_1;phase_3;phase_4之後，隱藏關是可以進入的，但是如果在phase_1或者phase_3二者之一加上密碼的時候，關卡可以通過，但是不能進入隱藏關，（也就是phase_4後面不加的話就不能進入隱藏關。）所以，第二種情況就是僅僅在phase_4之後加上隱藏關的密碼是可以進入隱藏關的，這也是結合組合分析出來的結果。

這裡我的猜想是，指標掃描，是一個個掃的，格式相同的後面加東西，指標應該會掃出來，而且還覺得是對的，但是在格式不一樣的後面加東西，指標就會認為你破解有誤（srds這是我的猜想，有不同意見的可以和我交流）


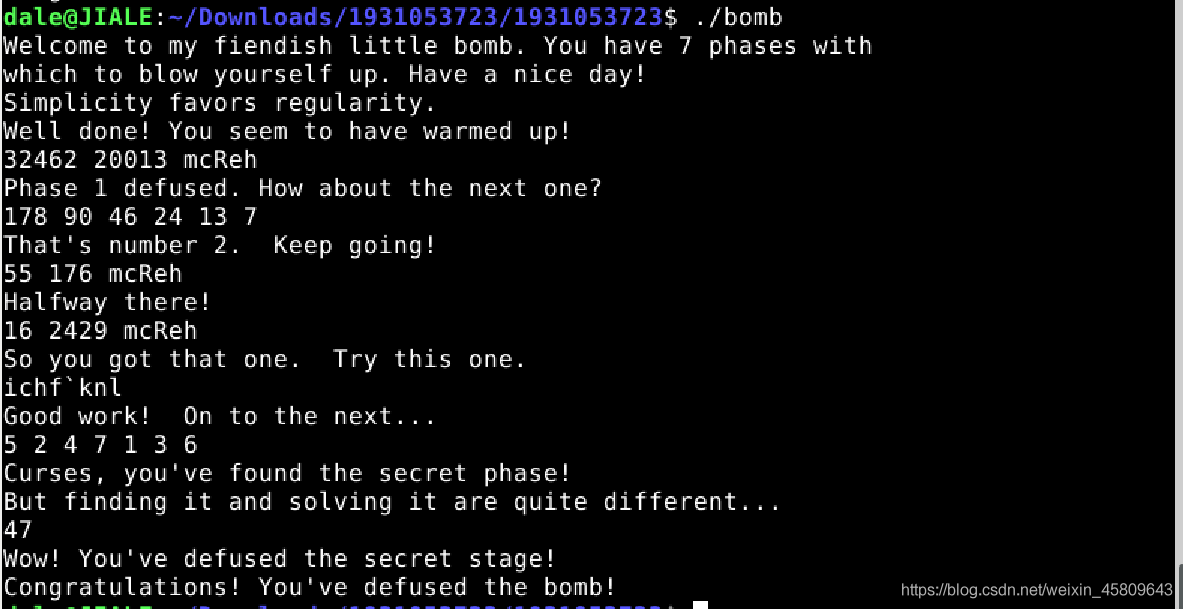
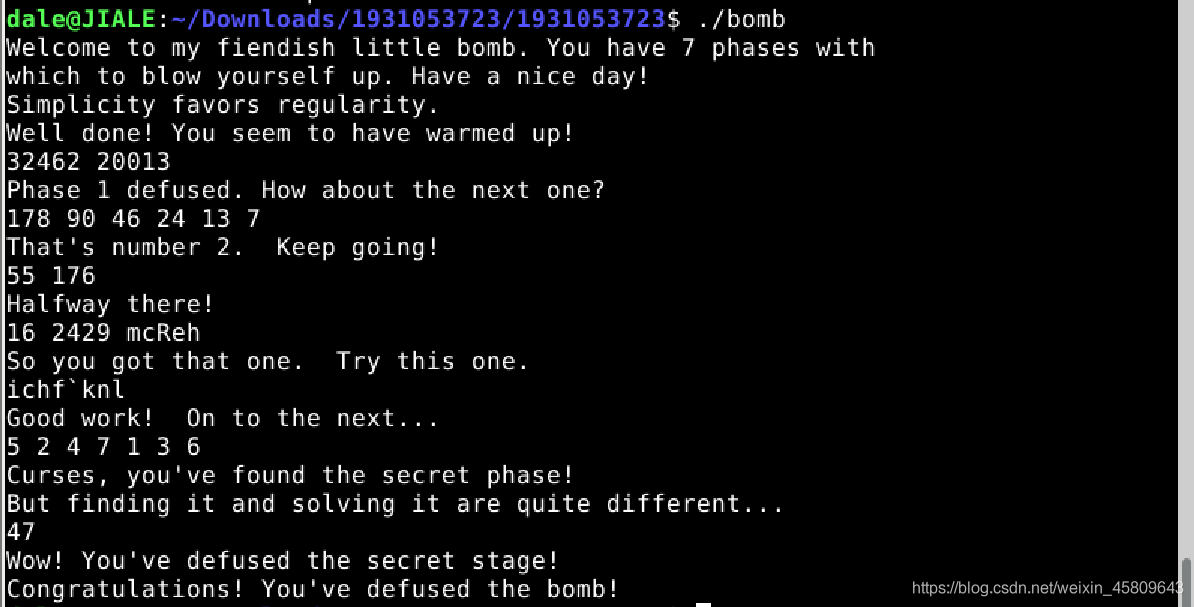
圖43 44 第一種和第二種情況的對比
（這裡就有我的猜想的驗證，不過不一定正確。）

衝向隱藏關
Secret_phase

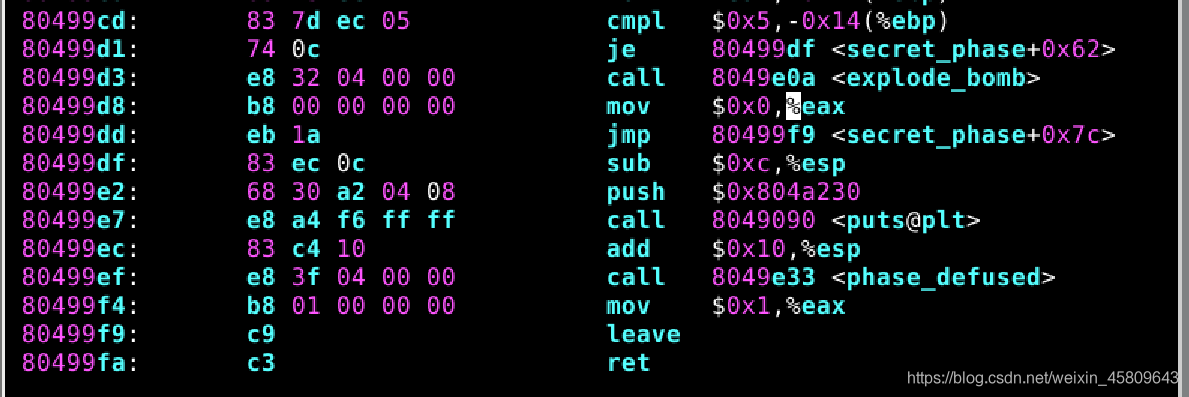
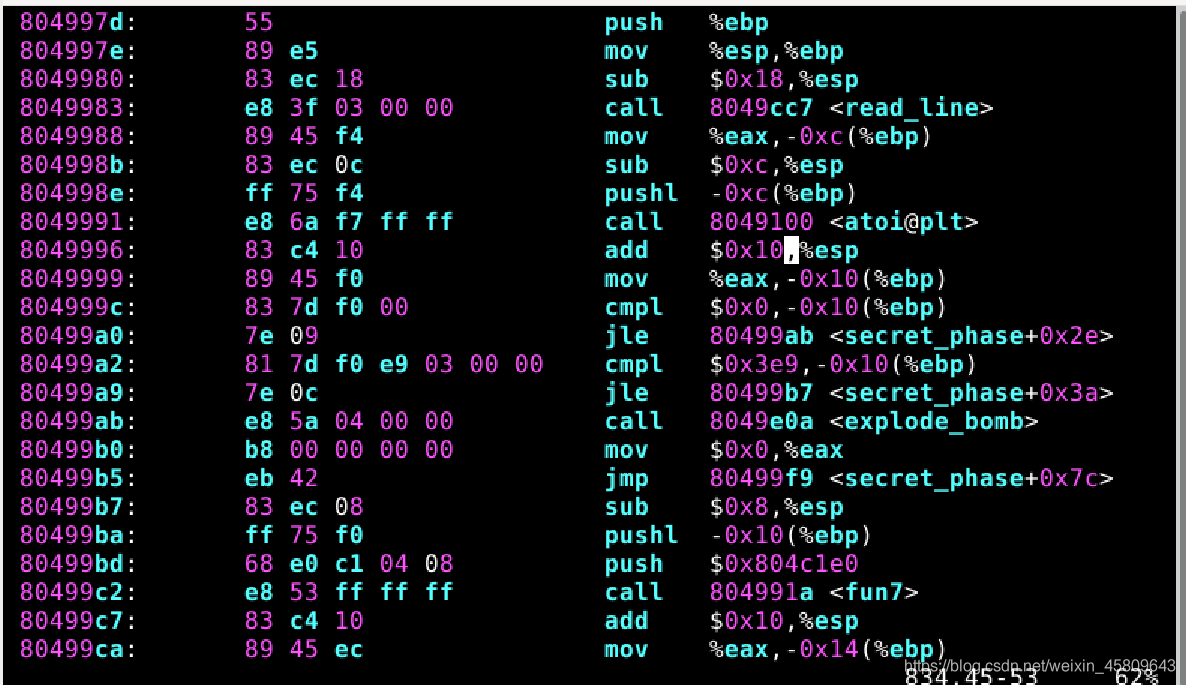
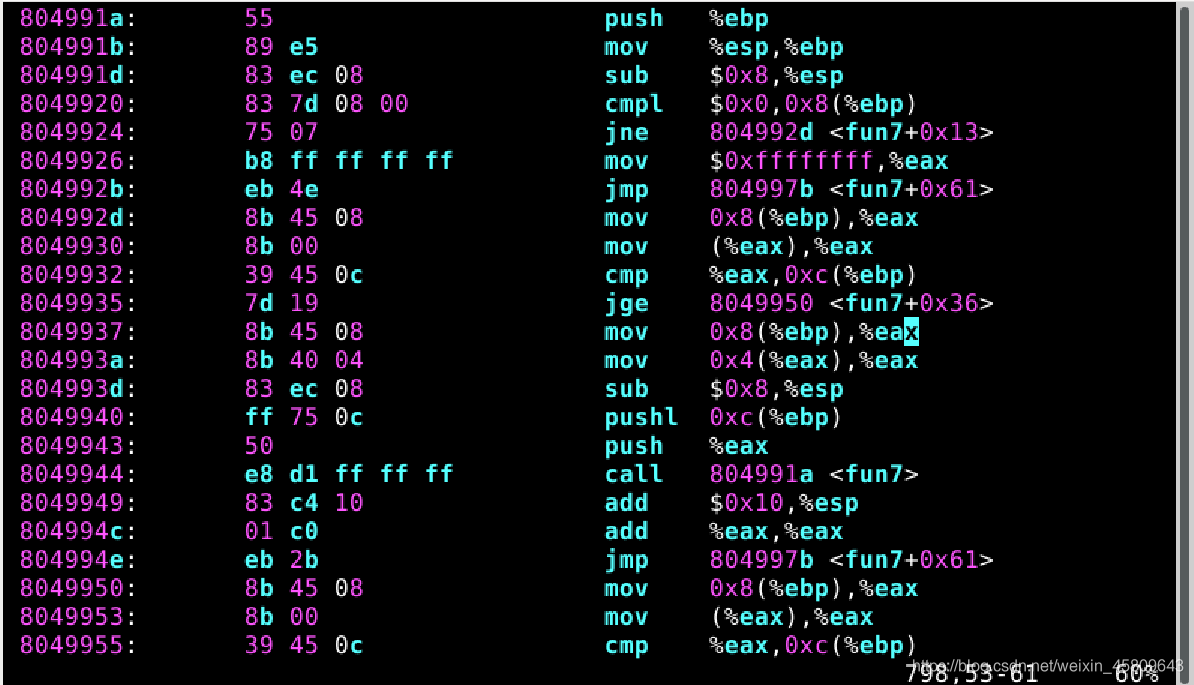
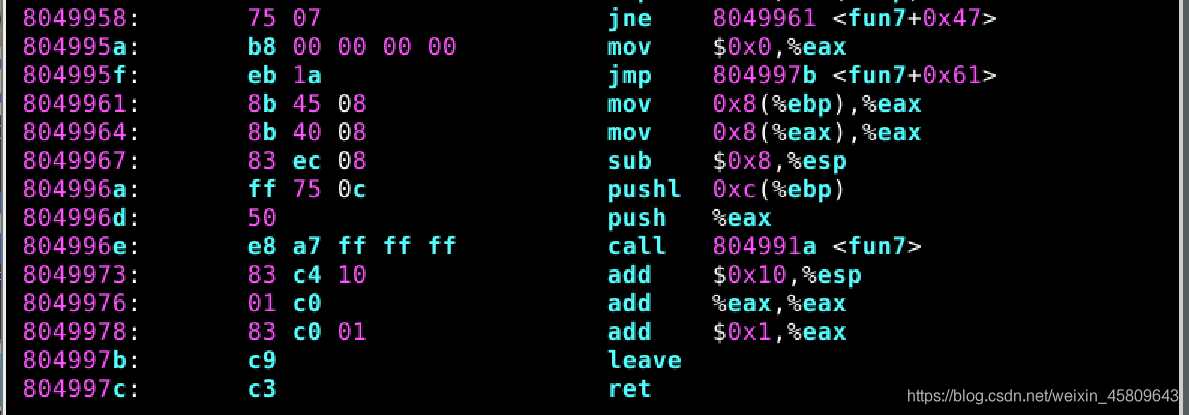圖45 46 47 48 隱藏關

這裡其實整的挺複雜，不過不要怕，咱們有gdb。
先找明地址，然後用gdb看看裡面是啥。

圖49 50 gdb檢視

然後我連帶著程式碼一起分析出了以下內容：

A2+1=5 - ->A=2 即有 * A<B
A2=2 -->A=1 有 * A>B
A*2+1=1 - ->A=0 即有 * A<B（假設fun7中呼叫的是A B）
三次遞迴中兩次執行了 「若 * A<B 將(A+8) 作為地址進入遞迴」系列程式碼，一次執行了 「若 * A>b，將(A+4) 作為地址進入遞迴」系列程式碼。使用 gdb 查詢儲存值,發現：
0x2f=47

驗證結果：
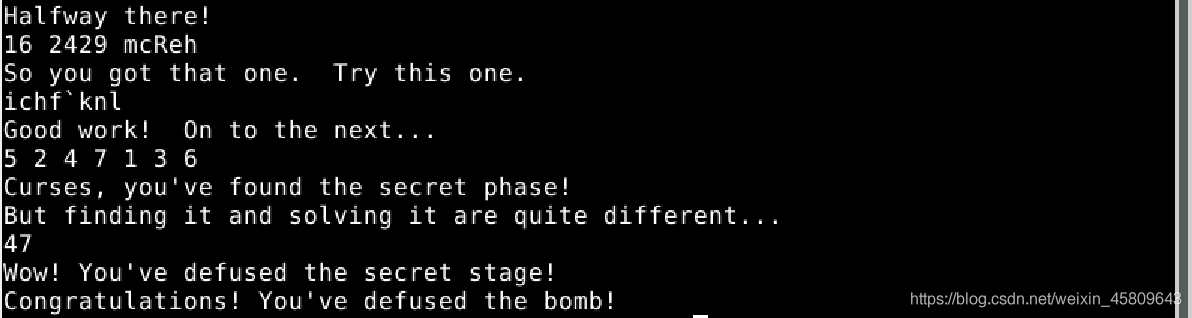圖51 隱藏關破解

隱藏關（secret_phase)已破解！！！

整體通關圖：
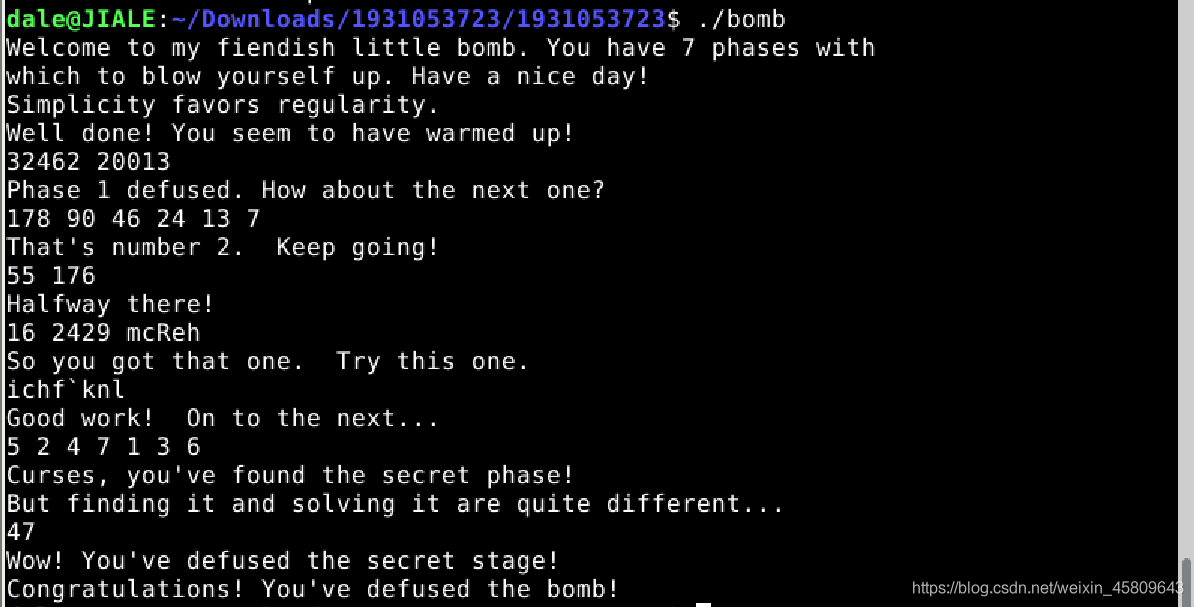圖52 正式通關

到這裡，所有的關卡都已經通過！！！

哇哈哈！二進位制炸彈破解正式結束啦！總而言之就是希望對大家有幫助，如果有人想和我一起討論這個實驗的話，歡迎和我一起來玩呀！
——張渣渣_