梯度下降法推導

**

梯度下降法公式推導

**

梯度下降法簡單的來說就是一種尋找最小值的點的方法，是機器學習和深度學習中常用的優化器，具體又可分為批次梯度下降（BGD）、隨機梯度下降（SGD）和小批次梯度下降（MBGD），本文不對這些問題做討論只是從數學角度來推導神經網路中的數學武器：梯度下降演演算法，本文是在學習湧井良幸先生的」深度學習的數學」一書後的筆記，僅用作個人學習和複習，由於筆者也是初學，所以難免會有各種錯誤，望各位大佬批評指正。
首先以二維函數舉例：

對這個函數使用梯度下降法的實質就是求如何沿最快路徑下降到最小值。
第一步研究當x和y變化是的z的變化情況：

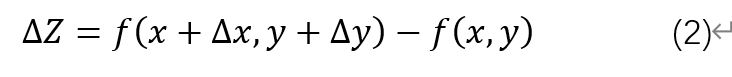
式2的近似公式為：

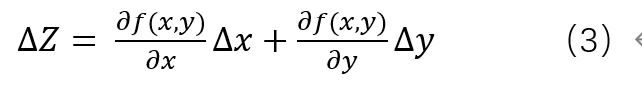
將式3用向量公式表示：


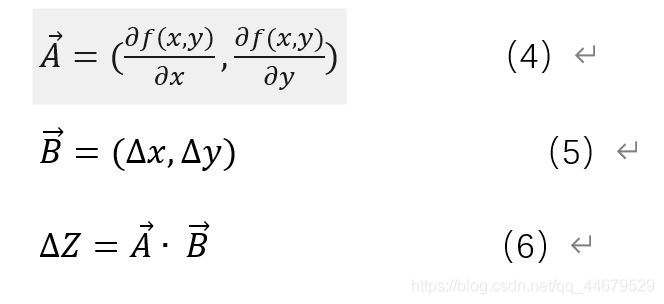
由向量內積公式有：


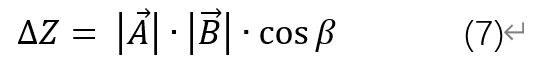
由於向量A和向量B方向相反所以必定存在一個正的微小常數η滿足下式：

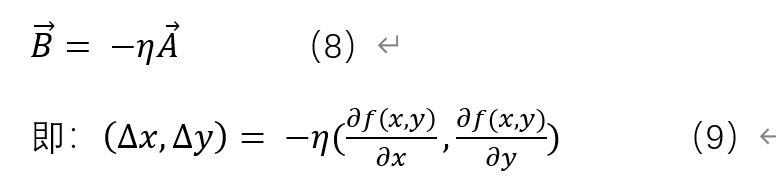
式9即為二維函數的梯度下降法公式
將式9從二維推廣到多維：

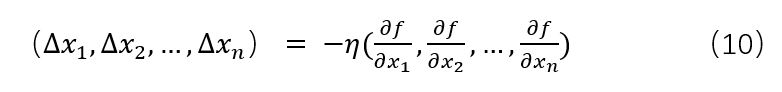
引入哈密頓運算元和位移向量：

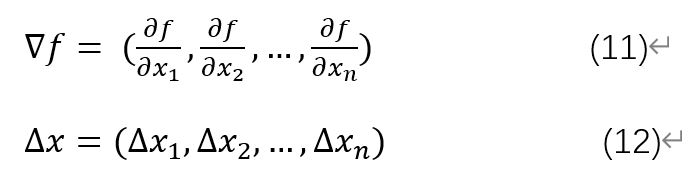
這樣式10就變為了：

式13即為梯度下降法的通用公式，式中的η可以看作步長，在神經網路中即為學習率。

至此，簡單的梯度下降法公式推導完成，當然，本文還有許多其他東西未涉及到，只是簡單的數學推導。本文是我的第一篇博文，是一個分享，也是對自己學習的記錄，方便以後複習，後續也會繼續分享一些自己之前做的筆記和新學習的內容，同時我也計劃做一個專題，專門用來記錄在學習李航老師的「統計學習方法「一書過程中的體會和心得，歡迎大家持續關注和批評指正。