爾康都能理解的辛普森悖論

本文地址：
https://goodgoodstudy.blog.csdn.net/article/details/108693838

資料分析中經常需要針對指標異動定位問題根源，第一反應當然是做拆分，總體出了問題就去查到底是哪個子模組除了問題。

如果指標是表示一個具有可加性的總量，如總人數、總銷量、總點選量，這時拆分到各個子模組上是沒有問題的，因為總指標等於各個子模組的指標之和。

但是當指標是一個均值或比例時，子模組的指標變化可能和總體的變化不一致，比如子模組的指標上升了，總體的指標卻下降了！

這就是 辛普森悖論。

舉個例子，某APP的每日人均發帖量 = 每日總貼數 / 總人數。現在發現這個指標下降了，我們按使用者的手機型別做個拆分：安卓使用者端和蘋果使用者端，卻發現：兩個使用者端的人均發帖量都上升了？？？？

這是為什麼呢？是統計出錯了嗎？還是計算公式抄錯了？

為了方便大家理解，我先舉個比較日常的例子。

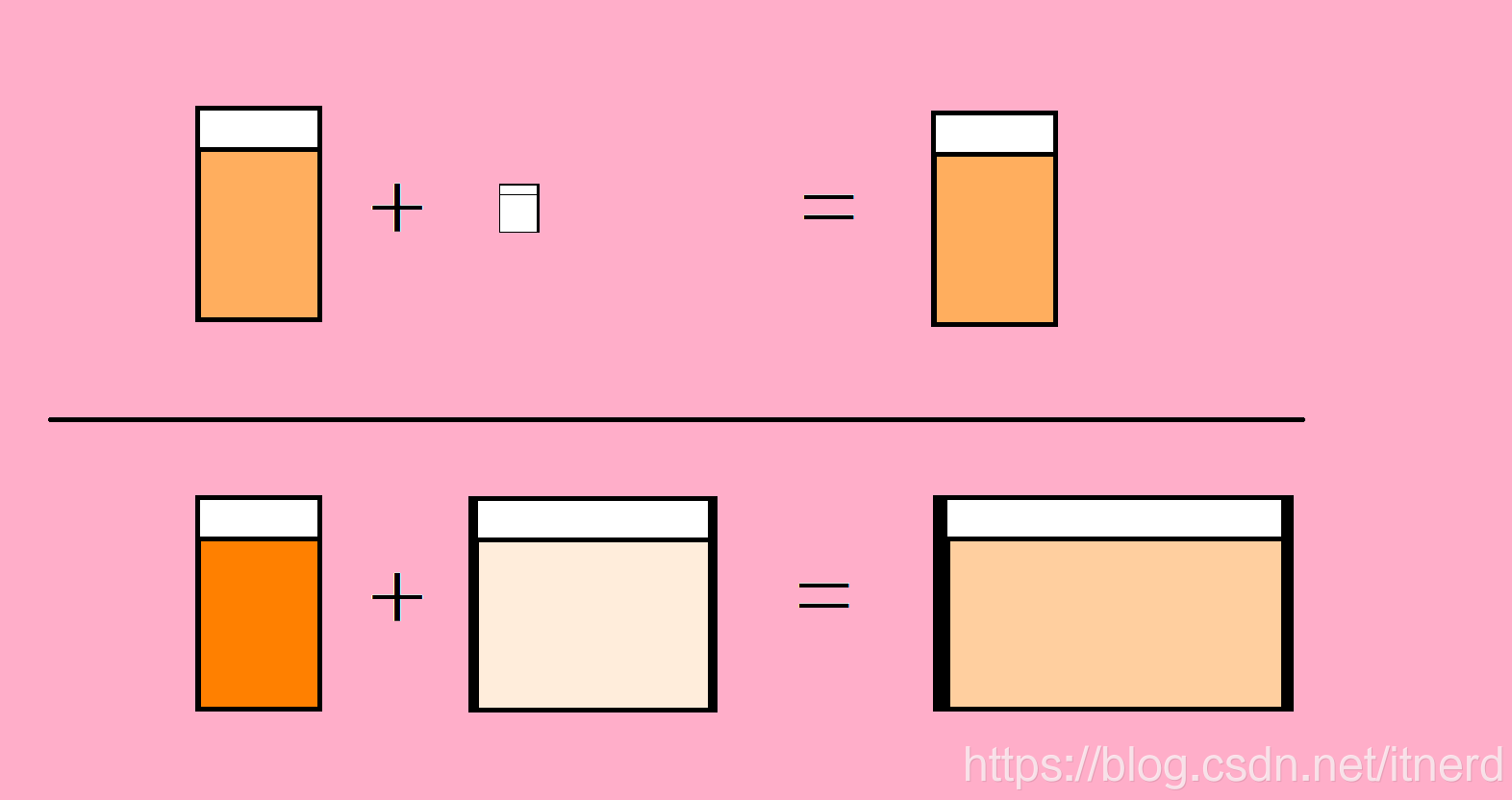
我有一杯很濃的橙汁，一杯很淡的橙汁，把它們混到一起，變成一壺濃度為 $C1$ 的橙汁

我有一杯很濃的橙汁，一壺很淡的橙汁，把它們混到一起，變成一缸濃度為 $C2$ 的橙汁

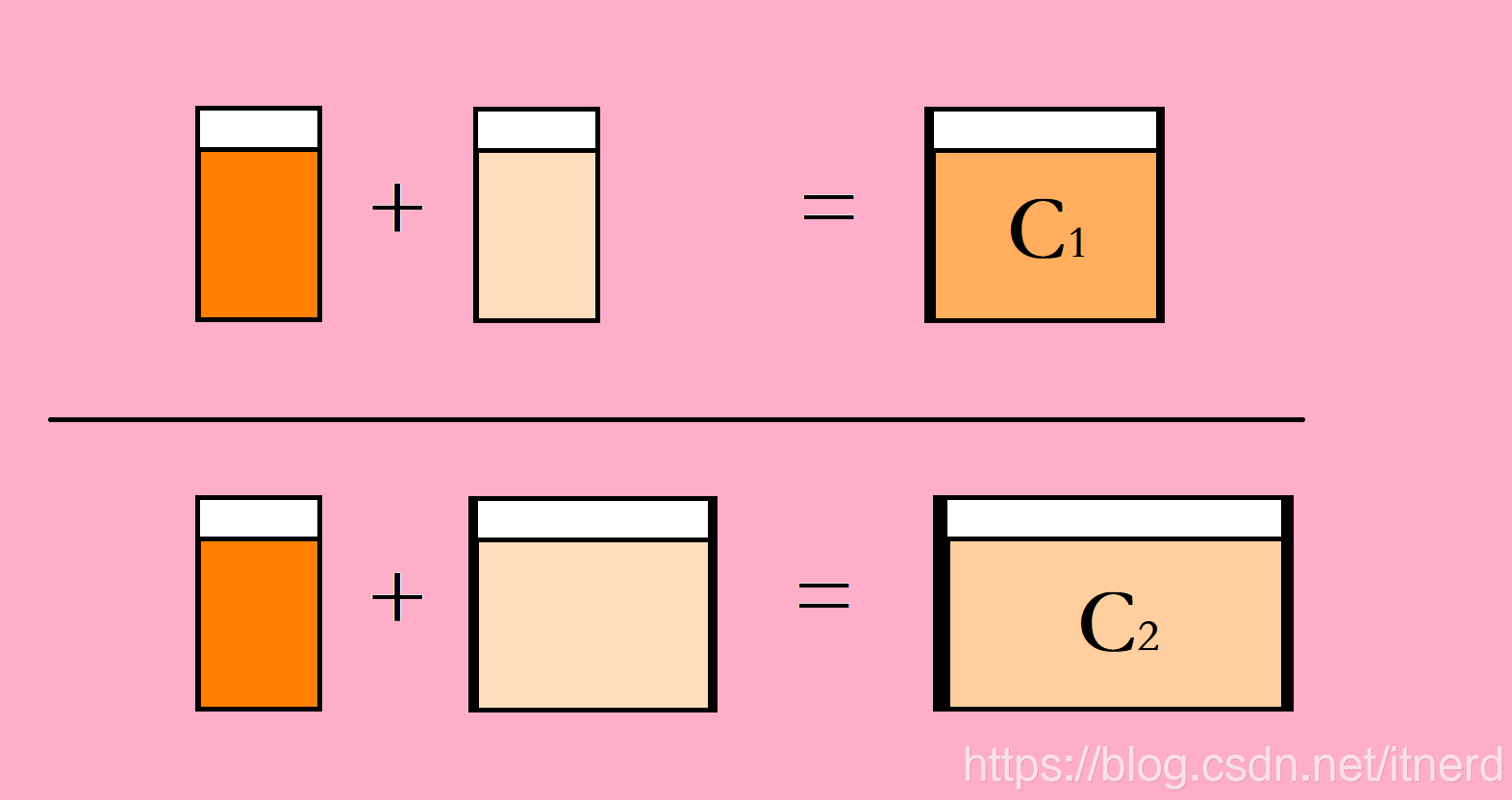
大家想一想，$C_1$和$C_2$那個濃度大呢？

大家是不是發現了其中的奧祕，濃橙汁和淡橙汁的濃度都沒變，但是混合到一起後，總濃度卻發生了變化

對應到資料分析的情景，各個子模組的指標都沒有變化，但是總指標卻下降了，為什麼呢？因為子模組中指標較低的模組的規模佔比變大了，使得總指標被拉低。

下面用更嚴謹的數學公式來說明：

假設總指標的計算式為：
$$c^{\ast }=\frac{m^{\ast }}{V^{\ast }}$$
第$i$個子模組的指標計算式為:
$$c_i=\frac{m_i}{V_i}$$
且滿足:
$$m^{\ast }=\sum _i{m}_i,V^{\ast }=\sum _i{V}_i$$

那麼總指標和各個子模組指標的關係為:
$$c^{\ast }=\frac{m^{\ast }}{V^{\ast }}=\frac{{\sum }_i{m}_i}{V^{\ast }}=\frac{{\sum }_i{c}_i{V}_i}{V^{\ast }}=\sum _i{c}_i{\omega }_i$$
其中，${\omega }_i=V_i/V^{\ast }$表示各個子模組分母的佔比。

容易理解，即使各個子模組的指標 $c_i$ 不變，各個模組的規模佔比 ${\omega }_i$ 發生變化，也會使總指標發生變化！

那如何理解各個子模組的指標上升，但是總指標卻下降了呢？

舉個極端的例子，以橙汁為例：

原來有一杯濃果汁和一滴淡果汁，混在一起，這杯濃果汁的濃度幾乎不變

現在稍稍提高了濃果汁的濃度，也微微提高了淡果汁的濃度，但是把淡果汁的體積從一滴變成了一壺，這下可好，果汁全被衝稀了，得到的一缸果汁濃度要低於原來的那杯濃果汁。