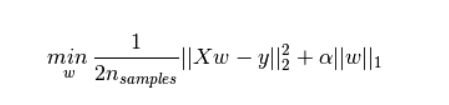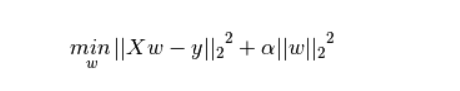正則化的簡單介紹

日期：2020-07-16

作者：18屆會長CYL

標籤：機器學習 正則化 作用 L1、L2

• 什麼是正則化（regularization）:

直觀感受為在損失函數後面新增一個額外項。通常該項為L1範數或者是L2範陣列成，又稱為L1正則化項和L2正則化項。（注：也有其他形式的正則化）

L1正則化項：權值向量w中各個元素的絕對值之和，再乘以係數

L2正則化項：權值向量w中各個元素的平方和開平方根，再乘以係數

• 正則化作用：

L1正則化：可以產生稀疏權值矩陣，即產生一個稀疏模型，可以用於特徵選擇（問題1：為什麼產生稀疏矩陣就可以用於特徵選擇，問題2：為什麼可以產生稀疏矩陣）
L2正則化：可以有助於防止模型過擬合（問題3：為什麼有助於防止過擬合）

• 解決問題

  • 問題1：稀疏矩陣與特徵選擇的關係：

  稀疏矩陣是指係數的稀疏矩陣，換句話說叫做權值的稀疏矩陣，也就是一個大部分權值都為0的矩陣。此矩陣表明，大部分特徵對這個模型無貢獻，或者貢獻比較小，那麼就可以篩查出來對模型有貢獻的神經元。

  • 問題2：為什麼可以產生稀疏矩陣（憑什麼加了個矩陣的係數和就可以讓無用權值置零）

  • 步驟1：化簡損失函數
    
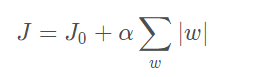
  • 步驟2：考慮只有兩個權值的情況w1,w2,那麼令L = α（|w1|+|w2|）。原式的數學意義轉化成在L的約束下求出J0的最小值解。（瘋狂思考這裡高數是怎麼學的）
  • 步驟3：圖解 圈圈是J0的等值線，菱形是L
    
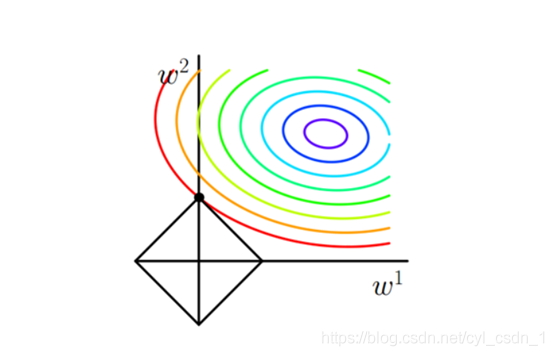
  • 步驟4：發現在最小值解的情況（第一次的交點，至於為什麼交點即最優，瘋狂思考高數問題）總是L的影象的尖尖的位置。（特點：座標軸，換句話說某特徵為0）

• 問題3、為什麼L2正則化有助於防止過擬合

  化簡步驟省略
  
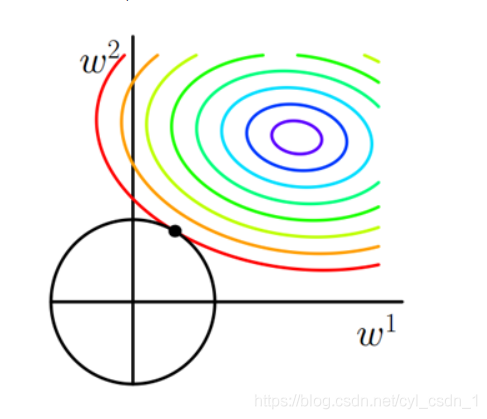
  觀察發現最優解部分大概率為非座標軸部分，那麼也就是所有的權值都不容易為0，（喪失了特徵選擇的優點），但是由於L2正則化可以讓引數都比較小，所以不容易過擬合（試想如果某一個引數權值特別大，那麼勢必一個輸入改變就會改變整個模型的輸出結果，換個理解方式是，模型「記住了這個值」，導致泛化能力垃圾的一批，抗擾動能力差，直觀表現就是訓練集正確率OK，但是測試集不OK，即過擬合），到這裡引申出來問題4：為什麼加入L2正則化可以讓最優解的引數普遍比較小

• 問題4：為什麼加入L2正則化可以讓最優解的引數普遍比較小

  • 梯度下降（複習）是讓權重沿著梯度的負方向進行「邁步」
  • 加上正則化項的梯度下降表示式變為：（λ為正則化項係數）
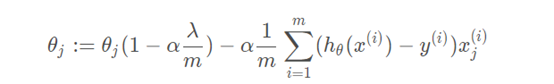
    不加正則化項的梯度下降表示式為：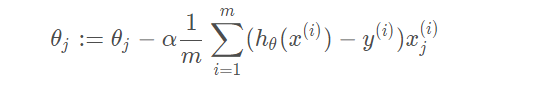
  • 可以看出每次梯度下降過程中，權重都會乘以一個小於1的數

多說一點關於正則化的結論:

L1正則化係數的選擇
• 係數越大越容易讓矩陣越稀疏
L2正則化係數的選擇
• 係數越大，權重衰減的越快，引數變得越小，太小的話會欠擬合，太大容易過擬合
正則化不止這兩種
• 還有一些 如 Dropout正則化 操作（AlexNet模型中使用） 後面結合AlexNet原始論文講解