【機器學習15】決策樹模型詳解
決策樹演演算法
手動反爬蟲: 原博地址
知識梳理不易,請尊重勞動成果,文章僅釋出在CSDN網站上,在其他網站看到該博文均屬於未經作者授權的惡意爬取資訊
如若轉載,請標明出處,謝謝!
前言
隨著人工智慧的不斷髮展,機器學習這門技術也越來越重要,很多人都開啟了學習機器學習,本文就介紹了機器學習的決策樹的詳細內容。
一、決策樹的概述
決策樹是一種樹形結構,其中每個內部節點表示一個屬性上的測試,每個分支代表一個測試輸出,每個葉子節點代表一種類別。
樹的組成:(如下圖示,來源百度,只做結構演示說明)
根節點:第一個選擇點
非葉子結點與分支:中間過程
葉子節點:最終的決策結果
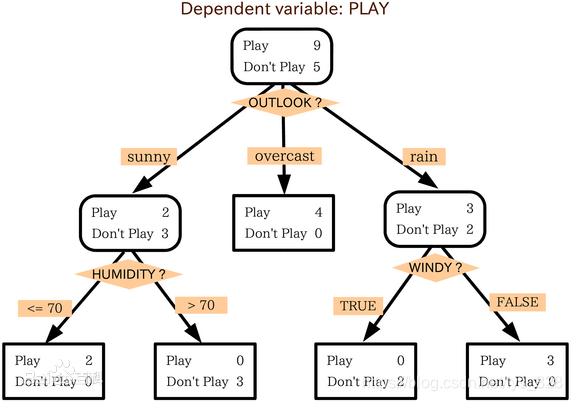
兩大特徵:從根節點開始一步步走到葉子節點(決策的過程)
所以的資料最終都會落到葉子節點,既可以做分類也可以做迴歸
實現決策樹的流程,下面以一個簡單的一家人是否愛玩遊戲進行劃分,如下
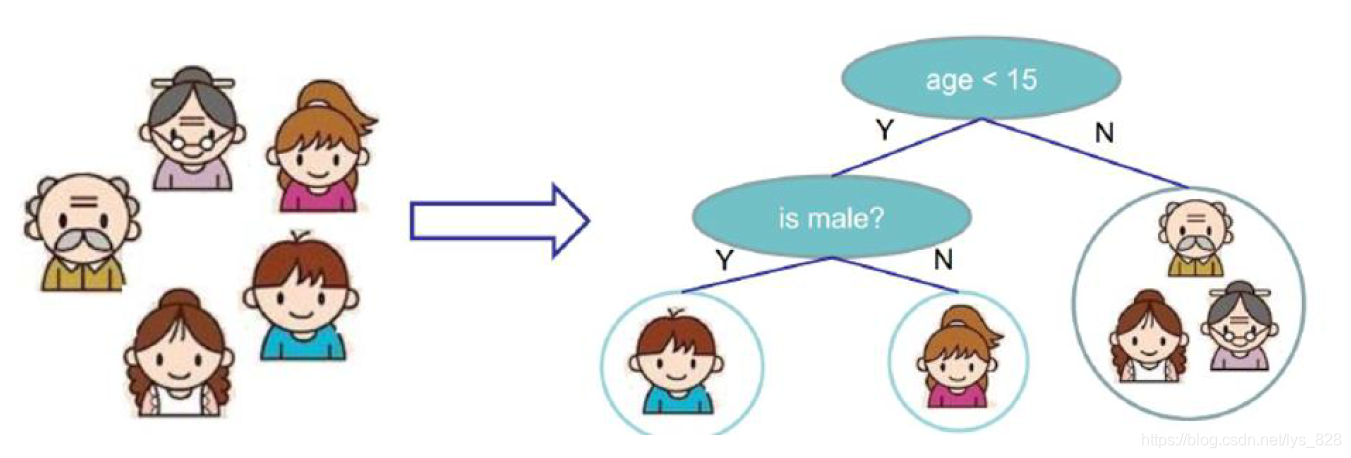
將一家人看做為是一份資料,輸入到決策樹中,首先會進行年齡的判斷是否大於15歲(人為主觀認定的數值),如果大於15,就判斷為有較小可能性玩遊戲,小於或等於15歲則認為有較大的可能性玩遊戲,然後再進行下一步細分,判斷性別,如果是男生則認為有較大的可能性玩遊戲,如果為女生則為較小的可能性喜歡玩遊戲。
這就是一個簡單的決策樹的過程,有點像最初python學習時的進行if-else成績好壞等級分類的程式。但是,決策樹這裡的分類的先後順序通常是不可以調換的,比如這裡為什麼要把年齡的判斷放在性別判斷前邊,就是因為希望第一次決策判斷就能實現大部分資料的篩選,儘可能的都做對了,然後再進行下一步,進而實現對上一步存在偏差資料的微調,因此根節點的重要性可想而知,其要實現對資料樣本大致的判斷,篩選出較為精確的資料。可以對比籃球比賽,當然是先上首發陣容,其次在考慮替補,針對於短板的地方進行補充。
那麼問題就來了?(根節點如何選擇)—— 憑什麼先按照年齡進行劃分,或者說憑什麼認為他們是首發嗎?
判斷的依據是啥???接下來呢?次根節點又如何進行切分呢???
二、熵的作用
目標:通過一種衡量標準,來計算通過不同特徵進行分支選擇後的分類情況,找出來最好的那個當成根節點,以此類推。
衡量標準-熵:熵是表示隨機變數不確定性的度量(解釋:說人話就是物體內部的混亂程度,比如義務雜貨市場裡面什麼都有那肯定混亂呀,專賣店裡面只賣一個牌子的那就穩定多啦)
舉個例子:如下,A中決策分類完成後一側是有三個三角二個圓,另一側是兩個三角一個圓,而B中決策分類後是一側是三角一側是圓,顯然是B方案的決策判斷更靠譜一些,用熵進行解釋就是熵值越小(混亂程度越低),決策的效果越好
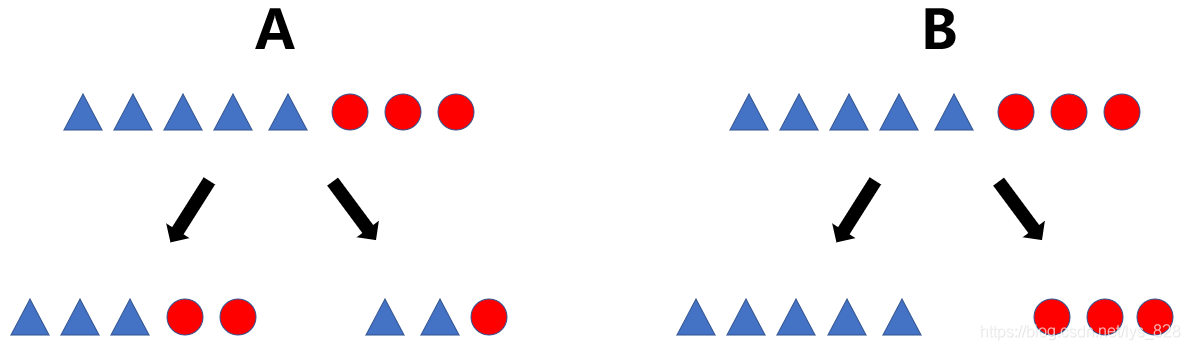
有些時候是可以憑藉的肉眼進行觀察的,但是大部分的決策結果並不能僅僅通過人為的評判,而需要一個量化的評判標準,於是就有了判斷公式:
H
(
X
)
=
−
∑
p
i
∗
l
o
g
(
p
i
)
,
i
=
1
,
2
,
.
.
.
,
n
H(X)=- ∑ p_{i}* log(p_{i}), i=1,2, ... , n
H(X)=−∑pi∗log(pi),i=1,2,...,n
這裡以上面的例子進行公式解讀,都只單看左側的分類結果,對於B中的,只有三角,也就是一個分類結果, p i p_{i} pi即為取值概率,這裡就為100%,再結合一下log函數,其值在[0,1]之間是遞增的,那麼前面加上一個負號就是遞減,因此這個B右側分類結果帶入計算公式值就是0,而0又是這個公式值中的最小值。再看A中左側的分類結果,由於存在著兩種情況,因此公式中就出現了累加,分別計算兩種結果的熵值情況,最後彙總,其值必然是大於0的,故A中的類別較多,熵值也就大了不少,B中的類別較為穩定(那麼在分類任務重我們希望通過節點分支後資料類別的熵值大還是小呢?)
其實都不是,在分類之前資料有一個熵值,在採用決策樹之後也會有熵值, 還拿A舉例,最初的狀態五個三角三個圓(對應一個熵值1),經過決策之後形成左側三個三角兩個圓(對應熵值2)和右側的兩個三角一個圓(對應熵值3),如果最後的熵值2+熵值3 < 熵值1,那麼就可以判定這次分類較好,比原來有進步,也就是通過對比熵值(不確定性)減少的程度判斷此次決策判斷的好壞,不是隻看分類後熵值的大小,而是要看決策前後熵值變化的情況。
為了方便記憶,於是有了 資訊增益 :表示特徵X使得類Y的不確定性減少的程度。(分類後的專一性,希望分類後的結果是同類在一起,比如上面希望把三角形分在一塊,圓形分在一塊)
三、決策樹構造範例
這裡使用官網提供的範例資料進行講解,資料為14天打球的情況(實際的情況);特徵為4種環境變化( x i x_{i} xi);最後的目標是希望構建決策樹實現最後是否打球的預測(yes|no),資料如下
x
1
:
x_{1}:
x1: outlook
x
2
:
x_{2}:
x2: temperature
x
3
:
x_{3}:
x3: humidity
x
4
:
x_{4}:
x4: windy
p l a y : play: play: yes|no
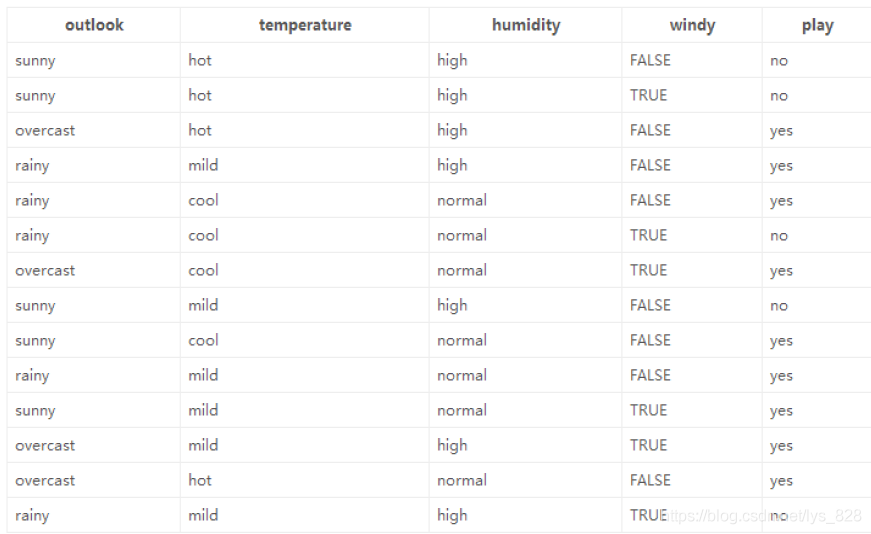
由資料可知共有4種特徵,因此在進行決策樹構建的時候根節點的選擇就有4種情況,如下。那麼就回到最初的問題上面了,到底哪個作為根節點呢?是否4種劃分方式均可以呢?因此 資訊增益 就要正式的出場露面了
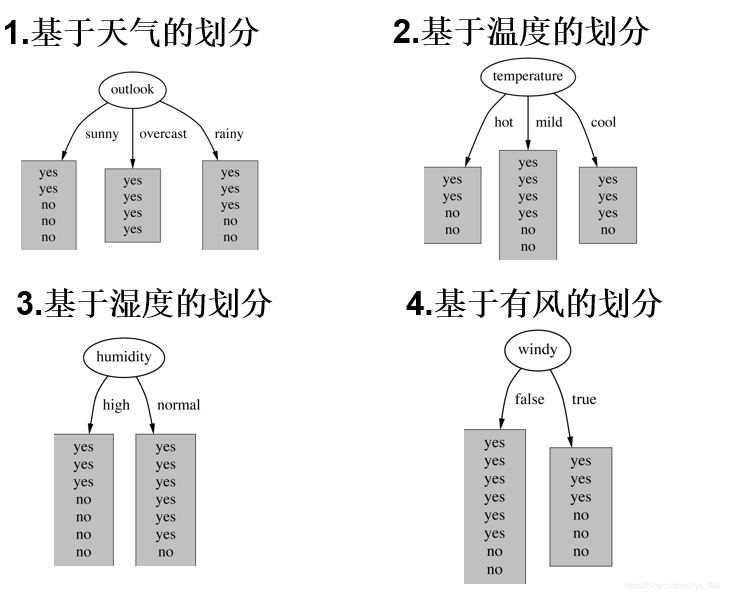
由於是要判斷決策前後的熵的變化,首先確定一下在歷史資料中(14天)有9天打球,5天不打球,所以此時的熵應為(一般log函數的底取2,要求計算的時候統一底數即可):
−
9
14
∗
l
o
g
2
9
14
−
5
14
∗
l
o
g
2
5
14
=
0.940
- \frac{9}{14}*log_{2}\frac{9}{14} - \frac{5}{14}*log_{2} \frac{5}{14} = 0.940
−149∗log2149−145∗log2145=0.940
先從第一個特徵下手,計算決策樹分類後的熵值的變化,還是使用公式進行計算
Outlook = sunny時,熵值為0.971 (
−
2
5
∗
l
o
g
2
2
5
−
3
5
∗
l
o
g
2
3
5
=
0.971
- \frac{2}{5}*log_{2}\frac{2}{5} - \frac{3}{5}*log_{2} \frac{3}{5} = 0.971
−52∗log252−53∗log253=0.971)
Outlook = overcast時,熵值為0
Outlook = rainy時,熵值為0.971(
−
3
5
∗
l
o
g
2
3
5
−
2
5
∗
l
o
g
2
2
5
=
0.971
- \frac{3}{5}*log_{2}\frac{3}{5} - \frac{2}{5}*log_{2} \frac{2}{5} = 0.971
−53∗log253−52∗log252=0.971)
注意:直接將計算得到的結果和上面計算出初始的結果相比較嗎? (當然不是,outlook取到sunny,overcast,rainy是有不同的概率的,因此最後的計算結果要考慮這個情況)
最終的熵值計算就為:
5
14
∗
0.971
+
0
+
5
14
∗
0.971
=
0.693
\frac{5}{14}*0.971 + 0 + \frac{5}{14}*0.971 = 0.693
145∗0.971+0+145∗0.971=0.693資訊增益:系統的熵值就由原始的0.940下降到了0.693,增益為
g
a
i
n
(
o
u
t
l
o
o
k
)
=
0.247
gain(outlook) = 0.247
gain(outlook)=0.247依次類推,可以分別求出剩下三種特徵分類的資訊增益如下:
g
a
i
n
(
t
e
m
p
e
r
a
t
u
r
e
)
=
0.029
,
g
a
i
n
(
h
u
m
i
d
i
t
y
)
=
0.152
,
g
a
i
n
(
w
i
n
d
y
)
=
0.048
gain(temperature) = 0.029, gain(humidity) = 0.152, gain(windy) = 0.048
gain(temperature)=0.029,gain(humidity)=0.152,gain(windy)=0.048最後我們選擇最大的那個就可以啦,相當於是遍歷了一遍特徵,找出來了根節點(老大),然後在其餘的中繼續通過資訊增益找子節點(老二)…,最終整個決策樹就構建完成了!
四、資訊增益率和gini係數
之前使用資訊增益進行判斷根節點有沒有什麼問題,或者是這種方法是不是存在bug,有些問題是解決不了的???答案是當然有的,比如還是使用上面的14個人打球的資料,這裡新增一個特徵為打球的次數ID,分別為1,2,3,…,12,13,14,那麼如果按照此特徵進行決策判斷,如下
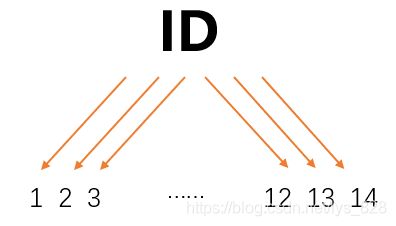
由此特徵進行決策判斷後的結果可以發現均為單個的分支,計算熵值的結果也就為0,這樣分類的結果資訊增益是最大的,說明這個特徵是非常有用的,如果還是按照資訊增益來進行評判,樹模型就勢必會按照ID進行根節點的選擇,而實際上按照這個方式進行決策判斷並不可行,只看每次打球的ID並不能說這一天是不是會打球。
從上面的範例中可以發現資訊增益無法解決這種特徵分類(類似ID)後結果特別特別多的情況,故就發展了另外的決策樹演演算法叫做 資訊增益率 和 gini係數
這裡介紹一下構建決策樹中使用的演演算法(至於前面的英文稱呼,知道是一種指代關係就可以了,比如說的資訊增益也可以使用ID3進行表示):
| 英文稱呼 | 中文稱呼 |
|---|---|
| ID3 | 資訊增益 (本身是存在著問題的) |
| C4.5 | 資訊增益率 (解決了ID3問題,考慮了自身熵) |
| CART | 使用gini係數作為衡量標準,計算公式: G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p) = \sum_{k=1}^{K}p_{k}(1-p_{k})=1- \sum_{k=1}^{K}p_{k}^{2} Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2 |
還是以14個人打球的資料,講解一下資訊增益率,這裡說考慮了自身熵,解決了ID3的問題是如何解決的呢?假設按照每次打球次數ID進行決策判斷,結果還是分為了14類,計算後的資訊增益為Q,從數值的大小上看一般是一個較小數值(0.940-0=0.940,絕對數值),但是對於其他資料特徵分類的結果來看這個數值又是很大(0.940相較於其他的gain數值,對比數值),這時候的資訊增益率就為 Q ( − 1 14 l o g 2 1 14 ) ∗ 14 \frac{Q}{(-\frac{1}{14}log_{2}\frac{1}{14})*14} (−141log2141)∗14Q,從對比數值來看,這個Q是很大,但是考慮到自身的熵值,參考一下log函數的影象,分母的值就是更大了,由此這個公式計算的數值(資訊增益率)就會很小,也就解決了資訊增益中無法處理分類後資料類別特別多的情況
gini係數計算公式和熵的衡量標準類似,只是計算方式不相同,這裡值越小代表這決策分類的效果越好,比如當p的累計值取1了,那麼最後結果就為0,當p取值較小時,經過平方後就更小了,由此計算的結果也就趨近1了
資訊增益率 是對根據熵值進行判定方式的改進,而 gini係數 則是另起爐灶,有著自己的計算方式
五、剪枝方法
首先明確一下為啥會有剪枝的操作,對比一下日常生活中的種植園工修理花草樹木,如果不管,任其生長,最後結果很可能是雜草灌木叢生,決策樹過擬合風險很大,理論上是可以完全分得開全部的資料,也就是樹會野蠻生長,每個葉子節點都會有一個資料,然後就把所有的資料全部分類完成
過擬合通俗的講就是:你在日常的測試做題或者考核的時候很好,但是一到大型的考試就不行了,這時候就存在邊看答案邊做題的現象,因此就可以把每道題都做對,就像決策樹一樣,可以無限的細分下去,滿足所有的分類結果,但是在最後預測的時候卻表現不好,故需要避免這種情況,也就需要進行剪枝,控制模型的複雜程度

剪枝策略:預剪枝(邊建立決策樹邊進行剪枝的操作,比較實用)、後剪枝(當建立完成後再進行剪枝操作)
預剪枝方式:限制深度(比如指定到某一具體數值後不再進行分裂)、葉子節點個數、葉子節點樣本數、資訊增益量等
後剪枝方式:通過一定的衡量標準,
C
α
(
T
)
=
C
(
T
)
+
α
∗
∣
T
l
e
a
f
∣
C_{\alpha}(T) = C(T) + \alpha*|T_{leaf}|
Cα(T)=C(T)+α∗∣Tleaf∣,葉子節點越多,損失越大
後剪枝的工作流程,比如選擇如下的節點,進行判斷其不分裂行不行? 不分裂的條件就是分裂之後的結果比分裂之前效果還要差勁。
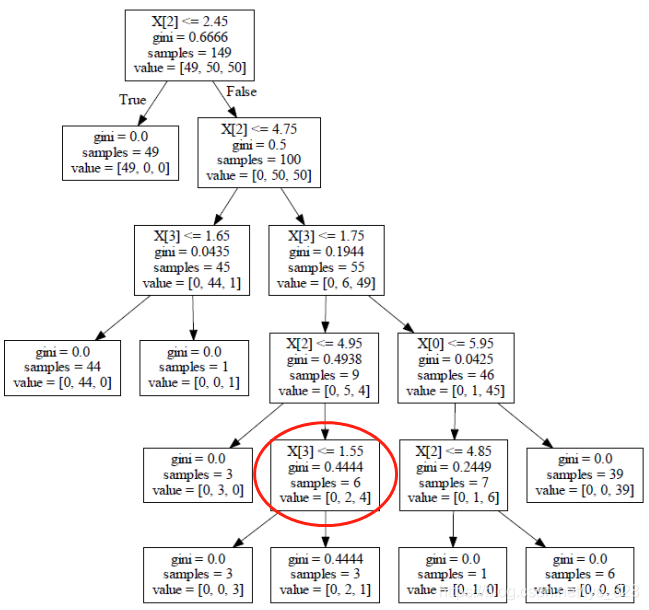
按照上面的計算公式,分裂之前 C α ( T ) = 0.444 ∗ 6 + 1 ∗ α C_{\alpha}(T) =0.444*6 + 1* \alpha Cα(T)=0.444∗6+1∗α分裂之後就是兩個葉子節點之和相加 C α ( T ) = 3 ∗ 0 + 1 ∗ α + 0.444 ∗ 3 + 1 ∗ α = 0.444 ∗ 3 + 2 ∗ α C_{\alpha}(T) =3*0+1* \alpha + 0.444*3+1* \alpha=0.444*3 + 2* \alpha Cα(T)=3∗0+1∗α+0.444∗3+1∗α=0.444∗3+2∗α最後就變成了比較這兩次取得的數值,值越大代表著損失越大,也就越不好,取值的大小是取決於我們給定的 α \alpha α值, α \alpha α值給出的越大,模型越會控制過擬合,值較小的時候是我們希望模型取得較好的結果,過不過擬合看的不是很重要
六、分類、迴歸任務
樹模型做分類任務,某個葉子節點中的型別是由什麼所決定的?還使用最初的圖示為例,樹模型是屬於有監督的演演算法,資料在輸入之前就已經有標籤的,比如下面「-」代表不玩遊戲。「+」代表玩遊戲,那麼右側紅框的分類結果中有三個「-」的資料,得到資料的眾數都是分類為「-」,所以之後如果有資料再分到此類別中,就都會被標記為「-」,故分類任務是有葉子節點中資料的眾數決定的,少數服從多數,加入某葉子節點中有10個「-」,2個「+」,則認定該葉子節點分類為「-」

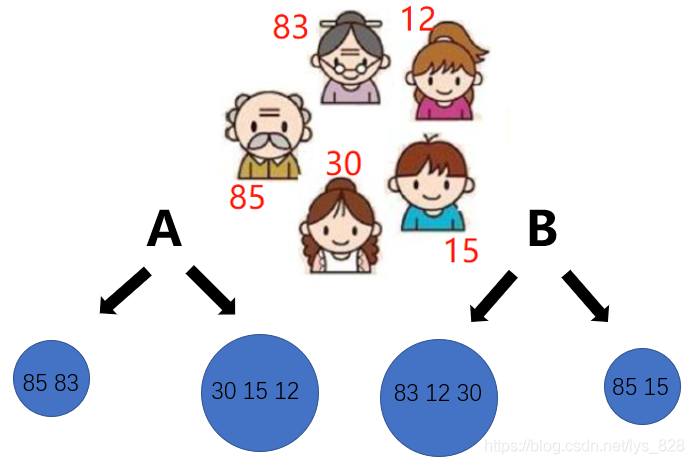
迴歸任務和分類任務的做法幾乎是一樣的,但是評估的方式是不一樣的,迴歸是採用方差進行衡量的,比如將上面的五個人按照年齡進行判斷,是否為老年人,根究A方案,顯然其方差要原小於B方案中的方差,也就是人為A方案中劃分方式更為合理。那麼既然是迴歸問題也就避免不了資料取值,葉子節點中的數值計算的方式就為各個資料的平均數,那麼接下來使用樹模型進行預測的時候,如果資料落入該葉子節點中數值即為此前計算的平均值,假如是A方案中的右側葉子節點,預測的結果數值就為(30+15+12) /3 =19
七、樹模型的視覺化展示
前期工作:下載可視乎的包:graphviz,並設定環境變數,檢驗前期工作完成的標識,在cmd命令列中輸入dot -version可以正常彈出如下資訊
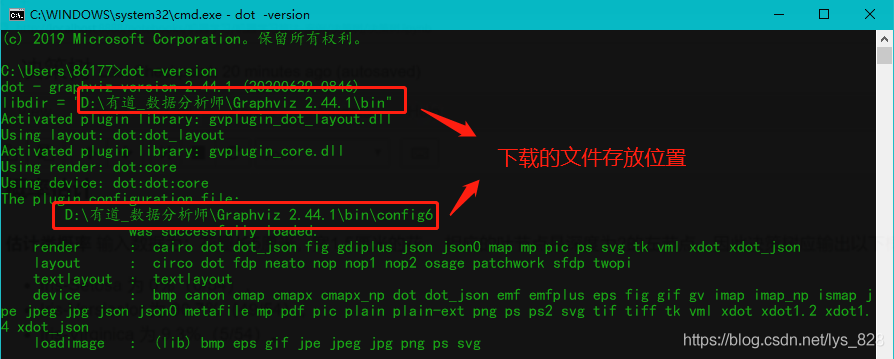
進入程式碼書寫,首先匯入相關的庫,書寫環境為jupyter notebook
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
第二步就是進行樹模型的建立
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris() #載入鳶尾花資料集
X = iris.data[:,2:] #這裡先選擇兩個特徵petal length and width(花瓣的長度和寬度)
y = iris.target #設定標籤
tree_clf = DecisionTreeClassifier(max_depth=2) #初始化樹模型並設定最大的深度為2
tree_clf.fit(X,y) #訓練樹模型
最後一步就是視覺化展示
from sklearn.tree import export_graphviz #這個就是剛剛下載的軟體
export_graphviz(
tree_clf, #第一個就是剛剛訓練好的樹模型
out_file="iris_tree.dot", #這裡指定輸出的檔案路徑和檔名稱
feature_names=iris.feature_names[2:], #畫圖中需要用到的特徵名稱,上面選擇兩個,這裡也是跟著一樣
class_names=iris.target_names, #標籤設定
rounded=True, #最後兩個預設即可
filled=True
)
執行上面程式碼後會在指定的檔案路徑下生成相應的檔案,然後,你可以使用graphviz包中的dot命令列工具將此.dot檔案轉換為各種格式,如PDF或PNG。下面這條命令列將.dot檔案轉換為.png影象檔案:dot -Tpng iris_tree.dot -o iris_tree.png
執行之後,就會在同路徑下生成指定格式的圖片
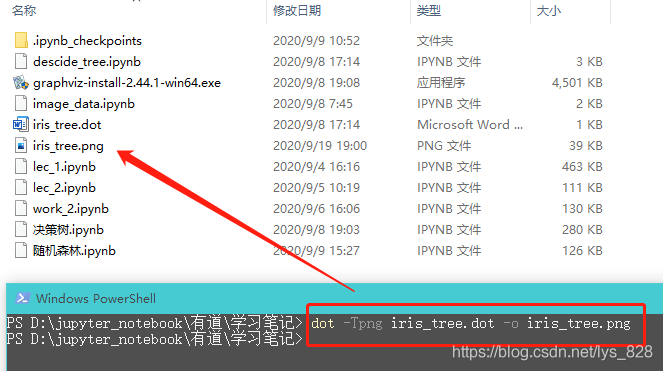
圖片開啟後如下,至此樹模型的視覺化的展示也就完成了,其中白色分塊中都有五行程式碼,第一行是指分類的條件,第二行是gini係數值,第三行是樣本資料量,第四行是原本三種類別的數量,最後一行是此次認定的資料分類結果
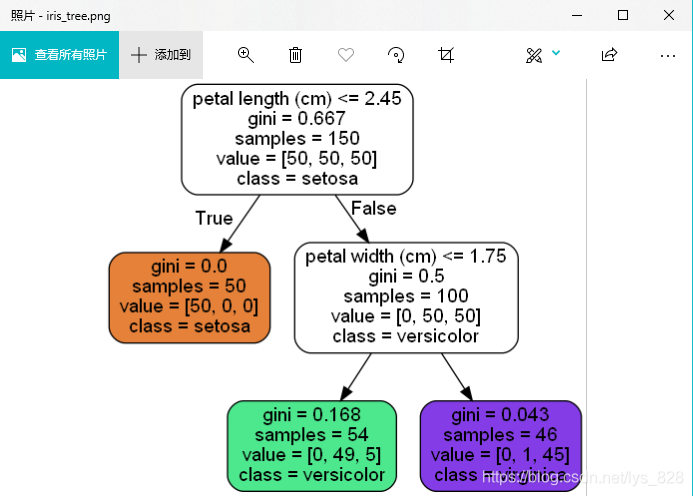
如果還想要將生成的圖片在jupyter notebook中進行內嵌輸出,可以使用如下程式碼
from IPython.display import Image
Image(filename='iris_tree.png',width=400,height=400)
八、決策邊界展示分析
概率計算:這裡舉個例子,加入輸入的資料為花瓣長5釐米,寬1.5釐米的花。 相應的葉節點是深度為2的左節點,因此決策樹應輸出以下概率(對照著上面的視覺化展示的樹模型圖)
Iris-Setosa 為 0%(0/54),
Iris-Versicolor 為 90.7%(49/54),
Iris-Virginica 為 9.3%(5/54)。
使用程式碼驗證一下
tree_clf.predict_proba([[5,1.5]])
輸出的結果為:
array([[0. , 0.90740741, 0.09259259]])
如果是直接預測類別
tree_clf.predict([[5,1.5]])
輸出的結果為:
array([1]) #這裡的1就代表是第二個類別,也就是Iris-Versicolor
將所有的資料結果進行視覺化展現
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
if plot_training:
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
plt.axis(axes)
if iris:
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
if legend:
plt.legend(loc="lower right", fontsize=14)
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
#下面這一部分是根據實際的決策樹的分類結果進行分類線的繪製
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
plt.title('Decision Tree decision boundaries')
plt.show()
輸出的結果為:(關於網格和刻度方向的顯示問題可以通過修改matplotlib庫的組態檔修改)
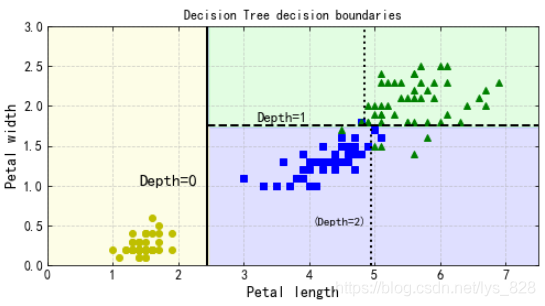
九、決策樹預剪枝常用引數
DecisionTreeClassifier類(sklearn的版本為0.23.1)還有一些其他引數類似地限制了決策樹的形狀:
min_samples_split(節點在分割之前必須具有的最小樣本數,預設為2),
min_samples_leaf(葉子節點必須具有的最小樣本數,預設為1),
max_leaf_nodes(葉子節點的最大數量),
max_features(在每個節點處評估用於拆分的最大特徵數,一般不限制)。
max_depth(樹最大的深度)
比如進行兩個樹模型不同引數的對比
from sklearn.datasets import make_moons
X,y = make_moons(n_samples=100,noise=0.25,random_state=53)
tree_clf1 = DecisionTreeClassifier(random_state=42)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4,random_state=42) #就只有一個引數不同,進行對比
tree_clf1.fit(X,y)
tree_clf2.fit(X,y)
plt.figure(figsize=(12,4))
plt.subplot(121)
plot_decision_boundary(tree_clf1,X,y,axes=[-1.5,2.5,-1,1.5],iris=False)
plt.title('No restrictions')
plt.subplot(122)
plot_decision_boundary(tree_clf2,X,y,axes=[-1.5,2.5,-1,1.5],iris=False)
plt.title('min_samples_leaf=4')
輸出的結果為:(可以發現不做任何限制的時候,模型過擬合了,而新增葉子節點最小樣本數引數後,模型變得更加可靠,也可以測試一下其他的引數)
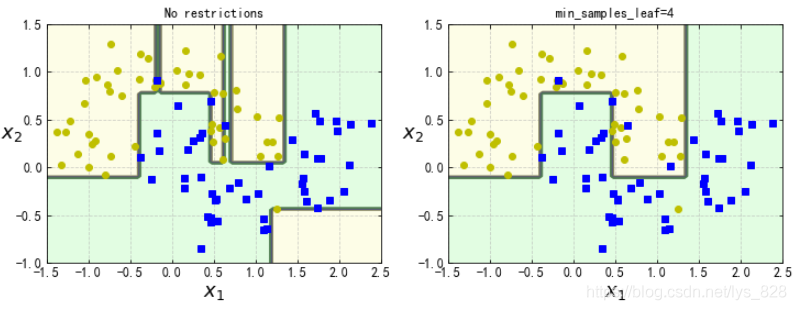
樹模型對資料的敏感,比如將資料的旋轉45度,那麼模型的決策邊界是會發生變化的
np.random.seed(6)
Xs = np.random.rand(100, 2) - 0.5
ys = (Xs[:, 0] > 0).astype(np.float32) * 2
angle = np.pi / 4
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xsr = Xs.dot(rotation_matrix)
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)
plt.figure(figsize=(11, 4))
#旋轉之前
plt.subplot(121)
plot_decision_boundary(tree_clf_s, Xs, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.title('Sensitivity to training set rotation')
#旋轉之後
plt.subplot(122)
plot_decision_boundary(tree_clf_sr, Xsr, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.title('Sensitivity to training set rotation')
plt.show()
輸出的結果為:(切記樹模型對資料是十分敏感的)
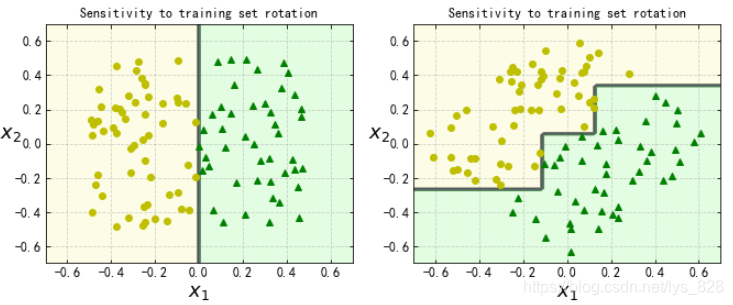
十、迴歸樹模型
迴歸任務,就像前文中介紹的一樣,迴歸和分類做法幾乎是一樣的,但是評估的方式是不一樣的,分類通過視覺化的樹模型中可以看出是採用gini係數,而回歸任務就是使用方差的平均數(mse:mean squared error)
#設定資料
np.random.seed(42)
m=200
X=np.random.rand(m,1)
y = 4*(X-0.5)**2
y = y + np.random.randn(m,1)/10
#訓練模型
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X,y)
#視覺化模型
export_graphviz(
tree_reg,
out_file=("regression_tree.dot"),
feature_names=["x1"],
rounded=True,
filled=True
)
#notebook中顯示
# 你的第二個決策樹長這樣
from IPython.display import Image
Image(filename="regression_tree.png",width=400,height=400,)
輸出的結果為:
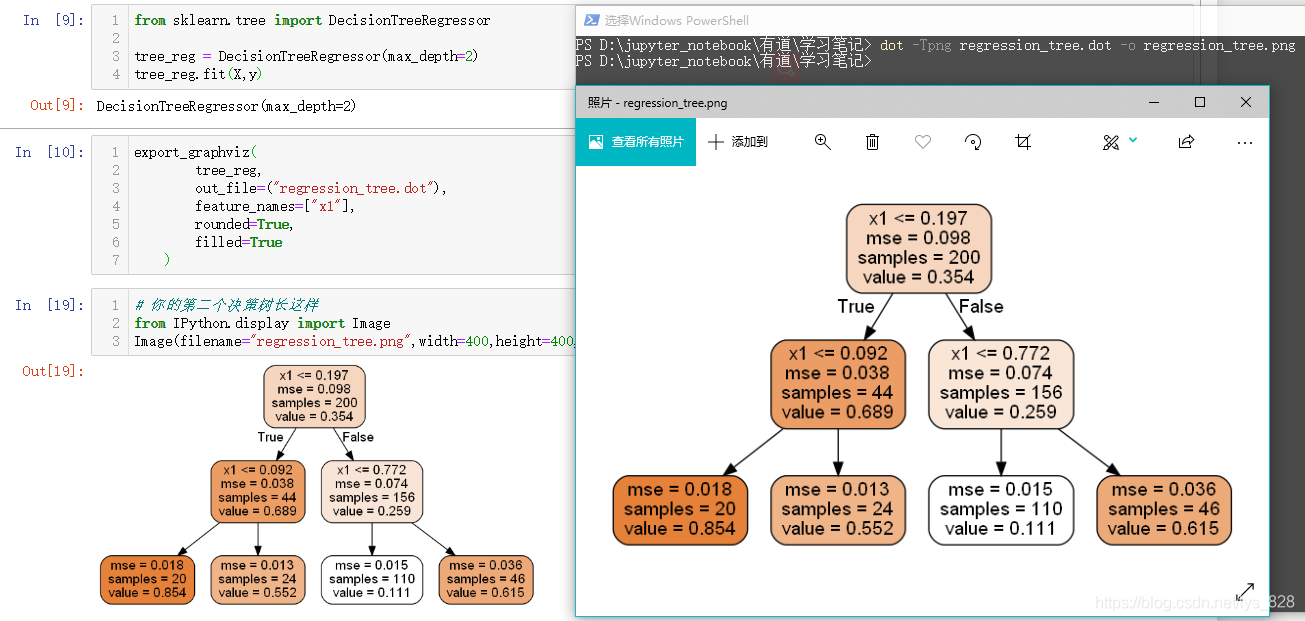
然後對比一下樹的深度對模型的影響,通過視覺化的圖形展示
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
y_pred = tree_reg.predict(x1)
plt.axis(axes)
plt.xlabel("$x_1$", fontsize=18)
if ylabel:
plt.ylabel(ylabel, fontsize=18, rotation=0)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)
plt.subplot(122)
plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "Depth=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)
plt.show()
輸出的結果為:
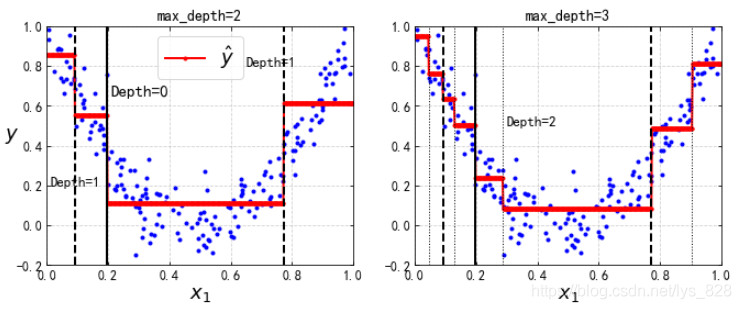
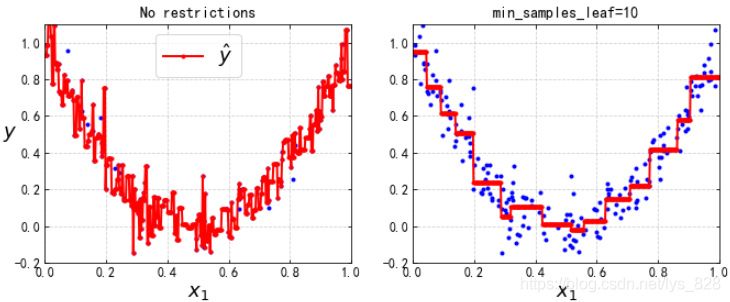
最後對比一下最小的葉子節點的樣本數量
tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)
plt.subplot(122)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf={}".format(tree_reg2.min_samples_leaf), fontsize=14)
plt.show()
輸出的結果為:(可以看出不約束預設情況下,樹模型會盡量擬合所有的點,但是改變引數數值後,模型變得橫平豎直的,也可以設定其他的常用的引數玩一玩)
至此關於迴歸樹模型的介紹就完畢了,撒花✿✿ヽ(°▽°)ノ✿
總結
文章中沒有對決策樹的由來和歷史進行過多的講解,直接有日常的小例子入手引入決策樹模型,並層層遞進式的講解決策樹中涉及的知識點,然後通過程式碼進行視覺化的展示,並以圖示的方式對比不同引數對於樹模型的影響,最後要注意的是決策樹不僅可以做分類也可以做迴歸任務