Scipy插值

在本章中，我們將討論插值，及如何在SciPy中使用它。

插值是什麼？

插值是在直線或曲線上的兩點之間找到值的過程。 為了幫助記住它的含義，我們應該將「inter」這個詞的第一部分想象為「輸入」，表示要檢視原來資料的「內部」。 這種插值工具不僅適用於統計學，而且在科學，商業或需要預測兩個現有資料點內的值時也很有用。

下面建立一些資料，看看如何使用scipy.interpolate包進行插值。

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print (x,y)

執行上面範例程式碼，得到以下結果 -

[ 0.          0.36363636  0.72727273  1.09090909  1.45454545  1.81818182
  2.18181818  2.54545455  2.90909091  3.27272727  3.63636364  4.        ] [-0.65364362 -0.61966189 -0.51077021 -0.31047698 -0.00715476  0.37976236
  0.76715099  0.99239518  0.85886263  0.27994201 -0.52586509 -0.99582185]

現在，有兩個陣列。 假設這兩個陣列作為空間點的兩個維度，使用下面的程式進行繪圖，並看看它們的樣子。

plt.plot(x, y,’o’)
plt.show()

上述程式將生成以下輸出 -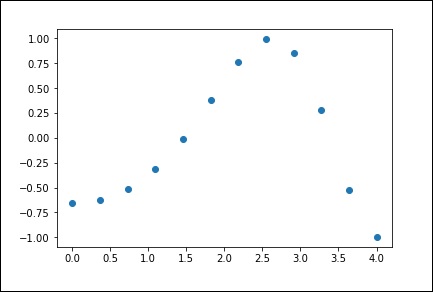

一維插值

scipy.interpolate中的interp1d類是一種建立基於固定資料點的函式的便捷方法，可以使用線性插值在給定資料定義的域內的任意位置評估該函式。

通過使用上述資料，建立一個插值函式並繪製一個新的插值圖。

f1 = interp1d(x, y,kind = 'linear')

f2 = interp1d(x, y, kind = 'cubic')

使用interp1d函式，建立了兩個函式f1和f2。 這些函式對於給定的輸入x返回y。 第三種變數型別表示插值技術的型別。 ‘線性’，’最近’，’零’，’線性’，’二次’，’立方’是一些插值技術。

現在，建立更多長度的新輸入以檢視插值的明顯區別。 對新資料使用舊資料的相同功能。

xnew = np.linspace(0, 4,30)

plt.plot(x, y, 'o', xnew, f1(xnew), '-', xnew, f2(xnew), '--')

plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')

plt.show()

上述程式將生成以下輸出 -

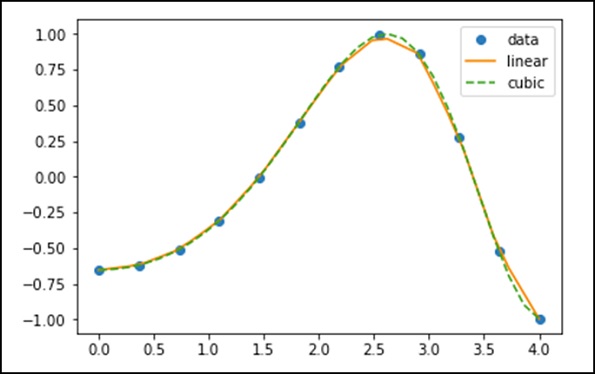
樣條曲線

為了通過資料點畫出平滑的曲線，繪圖員曾經使用薄的柔性木條，硬橡膠，金屬或塑料稱為機械樣條。 為了使用機械花鍵，在設計中沿著曲線明確選擇了一些銷釘，然後將花鍵彎曲，以便它們接觸到每個銷釘。

顯然，在這種結構下，樣條曲線在這些引腳上插入曲線。 它可以用來在其他圖紙中重現曲線。 引腳所在的點稱為結。 可以通過調整結點的位置來改變樣條線所定義的曲線的形狀。

單變數樣條

一維平滑樣條擬合一組給定的資料點。 Scipy.interpolate中的UnivariateSpline類是建立基於固定資料點類的函式的便捷方法 - scipy.interpolate.UnivariateSpline(x，y，w = None，bbox = [None，None]，k = 3，s = None，ext = 0，check_finite = False)。

下面來看看一個例子。

import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()

使用平滑引數的預設值。效果如下 -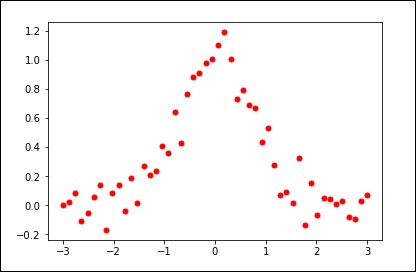

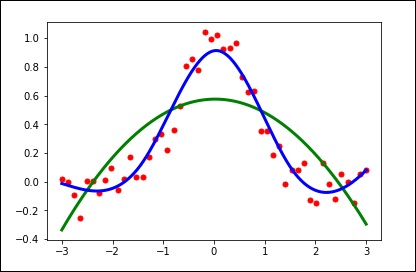
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()

手動更改平滑量。效果如下 -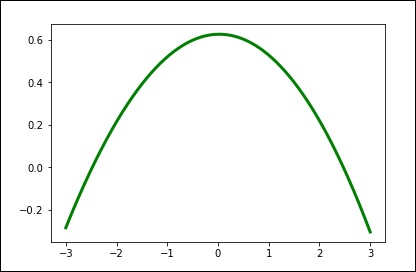

spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()

效果如下 -